So, let's sit down and start writing some numbers. For example:
You can write any numbers, and there can be as many of them as you like (in our case, there are them). No matter how many numbers we write, we can always tell which one is first, which is second, and so on until the last, that is, we can number them. This is an example of a number sequence:
Number sequence is a set of numbers, each of which can be assigned a unique number.
For example, for our sequence:
The assigned number is specific to only one number in the sequence. In other words, there are no three second numbers in the sequence. The second number (like the th number) is always the same.
The number with the number is called the nth member of the sequence.
We usually call the entire sequence by some letter (for example,), and each member of this sequence is the same letter with an index equal to the number of this member: .
In our case:

The most common types of progression are arithmetic and geometric. In this topic we will talk about the second type - geometric progression.
Why is geometric progression needed and its history?
Even in ancient times, the Italian mathematician monk Leonardo of Pisa (better known as Fibonacci) dealt with the practical needs of trade. The monk was faced with the task of determining what is the smallest number of weights that can be used to weigh a product? In his works, Fibonacci proves that such a system of weights is optimal: This is one of the first situations in which people had to deal with a geometric progression, which you have probably already heard about and have at least a general understanding of. Once you fully understand the topic, think about why such a system is optimal?
Currently, in life practice, geometric progression manifests itself when investing money in a bank, when the amount of interest is accrued on the amount accumulated in the account for the previous period. In other words, if you put money on a time deposit in a savings bank, then after a year the deposit will increase by the original amount, i.e. the new amount will be equal to the contribution multiplied by. In another year, this amount will increase by, i.e. the amount obtained at that time will again be multiplied by and so on. A similar situation is described in problems of calculating the so-called compound interest– the percentage is taken each time from the amount that is in the account, taking into account previous interest. We'll talk about these tasks a little later.
There are many more simple cases where geometric progression is applied. For example, the spread of influenza: one person infected another person, they, in turn, infected another person, and thus the second wave of infection is a person, and they, in turn, infected another... and so on...
By the way, a financial pyramid, the same MMM, is a simple and dry calculation based on the properties of a geometric progression. Interesting? Let's figure it out.
Geometric progression.
Let's say we have a number sequence:
You will immediately answer that this is easy and the name of such a sequence is with the difference of its members. How about this:

If you subtract the previous number from the subsequent number, you will see that each time you get a new difference (and so on), but the sequence definitely exists and is easy to notice - each subsequent number is times larger than the previous one!

This type of number sequence is called geometric progression and is designated.
Geometric progression () is a numerical sequence, the first term of which is different from zero, and each term, starting from the second, is equal to the previous one, multiplied by the same number. This number is called the denominator of a geometric progression.
The restrictions that the first term ( ) is not equal and are not random. Let's assume that there are none, and the first term is still equal, and q is equal to, hmm.. let it be, then it turns out:
Agree that this is no longer a progression.
As you understand, we will get the same results if there is any number other than zero, a. In these cases, there will simply be no progression, since the entire number series will either be all zeros, or one number, and all the rest will be zeros.
Now let's talk in more detail about the denominator of the geometric progression, that is, o.
Let's repeat: - this is the number how many times does each subsequent term change? geometric progression.
What do you think it could be? That's right, positive and negative, but not zero (we talked about this a little higher).
Let's assume that ours is positive. Let in our case, a. What is the value of the second term and? You can easily answer that:
That's right. Accordingly, if, then all subsequent terms of the progression have the same sign - they are positive.
What if it's negative? For example, a. What is the value of the second term and?
This is a completely different story
Try to count the terms of this progression. How much did you get? I have. Thus, if, then the signs of the terms of the geometric progression alternate. That is, if you see a progression with alternating signs for its members, then its denominator is negative. This knowledge can help you test yourself when solving problems on this topic.
Now let's practice a little: try to determine which number sequences are a geometric progression and which are an arithmetic progression:
Got it? Let's compare our answers:
- Geometric progression – 3, 6.
- Arithmetic progression – 2, 4.
- It is neither an arithmetic nor a geometric progression - 1, 5, 7.
Let's return to our last progression and try to find its member, just like in the arithmetic one. As you may have guessed, there are two ways to find it.
We successively multiply each term by.
So, the th term of the described geometric progression is equal to.
As you already guessed, now you yourself will derive a formula that will help you find any member of the geometric progression. Or have you already developed it for yourself, describing how to find the th member step by step? If so, then check the correctness of your reasoning.
Let us illustrate this with the example of finding the th term of this progression:

In other words:
Find the value of the term of the given geometric progression yourself.
Happened? Let's compare our answers:
Please note that you got exactly the same number as in the previous method, when we sequentially multiplied by each previous term of the geometric progression.
Let’s try to “depersonalize” this formula - let’s put it in general form and get:
The derived formula is true for all values - both positive and negative. Check this yourself by calculating the terms of the geometric progression with the following conditions: , a.
Did you count? Let's compare the results:
Agree that it would be possible to find a term of a progression in the same way as a term, however, there is a possibility of calculating incorrectly. And if we have already found the th term of the geometric progression, then what could be simpler than using the “truncated” part of the formula.
Infinitely decreasing geometric progression.
More recently, we talked about the fact that it can be either greater or less than zero, however, there are special values for which the geometric progression is called infinitely decreasing.
Why do you think this name is given?
First, let's write down some geometric progression consisting of terms.
Let's say, then:
We see that each subsequent term is less than the previous one by a factor, but will there be any number? You will immediately answer “no”. That is why it is infinitely decreasing - it decreases and decreases, but never becomes zero.
To clearly understand how this looks visually, let's try to draw a graph of our progression. So, for our case, the formula takes the following form:
On graphs we are accustomed to plotting dependence on, therefore:
The essence of the expression has not changed: in the first entry we showed the dependence of the value of a member of a geometric progression on its ordinal number, and in the second entry we simply took the value of a member of a geometric progression as, and designated the ordinal number not as, but as. All that remains to be done is to build a graph.
Let's see what you got. Here's the graph I came up with:

Do you see? The function decreases, tends to zero, but never crosses it, so it is infinitely decreasing. Let’s mark our points on the graph, and at the same time what the coordinate and means:

Try to schematically depict a graph of a geometric progression if its first term is also equal. Analyze what is the difference with our previous graph?
Did you manage? Here's the graph I came up with:

Now that you have fully understood the basics of the topic of geometric progression: you know what it is, you know how to find its term, and you also know what an infinitely decreasing geometric progression is, let's move on to its main property.
Property of geometric progression.
Do you remember the property of the terms of an arithmetic progression? Yes, yes, how to find the value of a certain number of a progression when there are previous and subsequent values of the terms of this progression. Do you remember? This:
Now we are faced with exactly the same question for the terms of a geometric progression. To derive such a formula, let's start drawing and reasoning. You'll see, it's very easy, and if you forget, you can get it out yourself.
Let's take another simple geometric progression, in which we know and. How to find? With arithmetic progression it is easy and simple, but what about here? In fact, there is nothing complicated in geometric either - you just need to write down each value given to us according to the formula.
You may ask, what should we do about it now? Yes, very simple. First, let's depict these formulas in a picture and try to do various manipulations with them in order to arrive at the value.
Let's abstract from the numbers that are given to us, let's focus only on their expression through the formula. We need to find the value highlighted in orange, knowing the terms adjacent to it. Let's try to perform various actions with them, as a result of which we can get.
Addition.
Let's try to add two expressions and we get:
From this expression, as you can see, we cannot express it in any way, therefore, we will try another option - subtraction.
Subtraction.
As you can see, we cannot express this either, therefore, let’s try to multiply these expressions by each other.
Multiplication.
Now look carefully at what we have by multiplying the terms of the geometric progression given to us in comparison with what needs to be found:
Guess what I'm talking about? Correctly, to find we need to take the square root of the geometric progression numbers adjacent to the desired one multiplied by each other:
Here you go. You yourself derived the property of geometric progression. Try to write this formula in general form. Happened?
Forgot the condition for? Think about why it is important, for example, try to calculate it yourself. What will happen in this case? That's right, complete nonsense because the formula looks like this:
Accordingly, do not forget this limitation.
Now let's calculate what it equals
Correct answer - ! If you didn’t forget the second possible value during the calculation, then you’re great and can immediately move on to training, and if you forgot, read what is discussed below and pay attention to why both roots must be written down in the answer.
Let's draw both of our geometric progressions - one with a value and the other with a value and check whether both of them have the right to exist:

In order to check whether such a geometric progression exists or not, it is necessary to see whether all its given terms are the same? Calculate q for the first and second cases.
See why we have to write two answers? Because the sign of the term you are looking for depends on whether it is positive or negative! And since we don’t know what it is, we need to write both answers with a plus and a minus.
Now that you have mastered the main points and derived the formula for the property of geometric progression, find, knowing and
Compare your answers with the correct ones:
What do you think, what if we were given not the values of the terms of the geometric progression adjacent to the desired number, but equidistant from it. For example, we need to find, and given and. Can we use the formula we derived in this case? Try to confirm or refute this possibility in the same way, describing what each value consists of, as you did when you originally derived the formula, at.
What did you get?
Now look carefully again.
and correspondingly:
From this we can conclude that the formula works not only with neighboring with the desired terms of the geometric progression, but also with equidistant from what the members are looking for.
Thus, our initial formula takes the form:
That is, if in the first case we said that, now we say that it can be equal to any natural number that is smaller. The main thing is that it is the same for both given numbers.
Practice with specific examples, just be extremely careful!
- , . Find.
- , . Find.
- , . Find.
Decided? I hope you were extremely attentive and noticed a small catch.
Let's compare the results.
In the first two cases, we calmly apply the above formula and get the following values:
In the third case, upon careful examination of the serial numbers of the numbers given to us, we understand that they are not equidistant from the number we are looking for: it is the previous number, but is removed at a position, so it is not possible to apply the formula.
How to solve it? It's actually not as difficult as it seems! Let us write down what each number given to us and the number we are looking for consists of.
So we have and. Let's see what we can do with them? I suggest dividing by. We get:
We substitute our data into the formula:
The next step we can find is - for this we need to take the cube root of the resulting number.
Now let's look again at what we have. We have it, but we need to find it, and it, in turn, is equal to:
We found all the necessary data for the calculation. Substitute into the formula:
Our answer: .
Try solving another similar problem yourself:
Given: ,
Find:
How much did you get? I have - .
As you can see, essentially you need remember just one formula- . You can withdraw all the rest yourself without any difficulty at any time. To do this, simply write the simplest geometric progression on a piece of paper and write down what each of its numbers is equal to, according to the formula described above.
The sum of the terms of a geometric progression.
Now let's look at formulas that allow us to quickly calculate the sum of terms of a geometric progression in a given interval:
To derive the formula for the sum of terms of a finite geometric progression, multiply all parts of the above equation by. We get:
Look carefully: what do the last two formulas have in common? That's right, common members, for example, and so on, except for the first and last member. Let's try to subtract the 1st from the 2nd equation. What did you get?
Now express the term of the geometric progression through the formula and substitute the resulting expression into our last formula:
Group the expression. You should get:
All that remains to be done is to express:
Accordingly, in this case.
What if? What formula works then? Imagine a geometric progression at. What is she like? A series of identical numbers is correct, so the formula will look like this:
There are many legends about both arithmetic and geometric progression. One of them is the legend of Set, the creator of chess.
Many people know that the game of chess was invented in India. When the Hindu king met her, he was delighted with her wit and the variety of positions possible in her. Having learned that it was invented by one of his subjects, the king decided to personally reward him. He summoned the inventor to himself and ordered him to ask him for everything he wanted, promising to fulfill even the most skillful desire.
Seta asked for time to think, and when the next day Seta appeared before the king, he surprised the king with the unprecedented modesty of his request. He asked to give a grain of wheat for the first square of the chessboard, a grain of wheat for the second, a grain of wheat for the third, a fourth, etc.
The king was angry and drove Seth away, saying that the servant's request was unworthy of the king's generosity, but promised that the servant would receive his grains for all the squares of the board.
And now the question: using the formula for the sum of the terms of a geometric progression, calculate how many grains Seth should receive?
Let's start reasoning. Since, according to the condition, Seth asked for a grain of wheat for the first square of the chessboard, for the second, for the third, for the fourth, etc., then we see that the problem is about a geometric progression. What does it equal in this case?
Right.
Total squares of the chessboard. Respectively, . We have all the data, all that remains is to plug it into the formula and calculate.
To imagine at least approximately the “scale” of a given number, we transform using the properties of degree:
Of course, if you want, you can take a calculator and calculate what number you end up with, and if not, you’ll have to take my word for it: the final value of the expression will be.
That is:
quintillion quadrillion trillion billion million thousand.
Phew) If you want to imagine the enormity of this number, then estimate how large a barn would be required to accommodate the entire amount of grain.
If the barn is m high and m wide, its length would have to extend for km, i.e. twice as far as from the Earth to the Sun.
If the king were strong in mathematics, he could have invited the scientist himself to count the grains, because to count a million grains, he would need at least a day of tireless counting, and given that it is necessary to count quintillions, the grains would have to be counted throughout his life.
Now let’s solve a simple problem involving the sum of terms of a geometric progression.
A student of class 5A Vasya fell ill with the flu, but continues to go to school. Every day Vasya infects two people, who, in turn, infect two more people, and so on. There are only people in the class. In how many days will the whole class be sick with the flu?
So, the first term of the geometric progression is Vasya, that is, a person. The th term of the geometric progression is the two people he infected on the first day of his arrival. The total sum of the progression terms is equal to the number of 5A students. Accordingly, we talk about a progression in which:
Let's substitute our data into the formula for the sum of the terms of a geometric progression:
The whole class will get sick within days. Don't believe formulas and numbers? Try to portray the “infection” of students yourself. Happened? Look how it looks for me:

Calculate for yourself how many days it would take for students to get sick with the flu if each one infected a person, and there were only one person in the class.
What value did you get? It turned out that everyone started getting sick after a day.
As you can see, such a task and the drawing for it resemble a pyramid, in which each subsequent one “brings” new people. However, sooner or later a moment comes when the latter cannot attract anyone. In our case, if we imagine that the class is isolated, the person from closes the chain (). Thus, if a person were involved in a financial pyramid in which money was given if you brought two other participants, then the person (or in general) would not bring anyone, accordingly, would lose everything that they invested in this financial scam.
Everything that was said above refers to a decreasing or increasing geometric progression, but, as you remember, we have a special type - an infinitely decreasing geometric progression. How to calculate the sum of its members? And why does this type of progression have certain characteristics? Let's figure it out together.
So, first, let's look again at this drawing of an infinitely decreasing geometric progression from our example:

Now let’s look at the formula for the sum of a geometric progression, derived a little earlier:
or
What are we striving for? That's right, the graph shows that it tends to zero. That is, at, will be almost equal, respectively, when calculating the expression we will get almost. In this regard, we believe that when calculating the sum of an infinitely decreasing geometric progression, this bracket can be neglected, since it will be equal.
- formula is the sum of the terms of an infinitely decreasing geometric progression.
IMPORTANT! We use the formula for the sum of terms of an infinitely decreasing geometric progression only if the condition explicitly states that we need to find the sum infinite number of members.
If a specific number n is specified, then we use the formula for the sum of n terms, even if or.
Now let's practice.
- Find the sum of the first terms of the geometric progression with and.
- Find the sum of the terms of an infinitely decreasing geometric progression with and.
I hope you were extremely careful. Let's compare our answers:
Now you know everything about geometric progression, and it’s time to move from theory to practice. The most common geometric progression problems encountered on the exam are problems calculating compound interest. These are the ones we will talk about.
Problems on calculating compound interest.
You've probably heard of the so-called compound interest formula. Do you understand what it means? If not, let’s figure it out, because once you understand the process itself, you will immediately understand what geometric progression has to do with it.
We all go to the bank and know that there are different conditions for deposits: this is the term, and additional services, and interest with two different ways of calculating it - simple and complex.
WITH simple interest everything is more or less clear: interest is accrued once at the end of the deposit term. That is, if we say that we deposit 100 rubles for a year, then they will be credited only at the end of the year. Accordingly, by the end of the deposit we will receive rubles.
Compound interest- this is an option in which it happens interest capitalization, i.e. their addition to the deposit amount and subsequent calculation of income not from the initial, but from the accumulated deposit amount. Capitalization does not occur constantly, but with some frequency. As a rule, such periods are equal and most often banks use a month, quarter or year.
Let’s assume that we deposit the same rubles annually, but with monthly capitalization of the deposit. What are we doing?
Do you understand everything here? If not, let's figure it out step by step.
We brought rubles to the bank. By the end of the month, we should have an amount in our account consisting of our rubles plus interest on them, that is:
Agree?
We can take it out of brackets and then we get:
Agree, this formula is already more similar to what we wrote at the beginning. All that's left is to figure out the percentages
In the problem statement we are told about annual rates. As you know, we do not multiply by - we convert percentages to decimal fractions, that is:
Right? Now you may ask, where did the number come from? Very simple!
I repeat: the problem statement says about ANNUAL interest that accrues MONTHLY. As you know, in a year of months, accordingly, the bank will charge us a portion of the annual interest per month:
Realized it? Now try to write what this part of the formula would look like if I said that interest is calculated daily.
Did you manage? Let's compare the results:

Well done! Let's return to our task: write how much will be credited to our account in the second month, taking into account that interest is accrued on the accumulated deposit amount.
Here's what I got:
Or, in other words:

I think that you have already noticed a pattern and saw a geometric progression in all this. Write what its member will be equal to, or, in other words, what amount of money we will receive at the end of the month.
Did? Let's check!
As you can see, if you put money in the bank for a year at a simple interest rate, you will receive rubles, and if at a compound interest rate, you will receive rubles. The benefit is small, but this only happens during the th year, but for a longer period capitalization is much more profitable:

Let's look at another type of problem involving compound interest. After what you have figured out, it will be elementary for you. So, the task:
The Zvezda company began investing in the industry in 2000, with capital in dollars. Every year since 2001, it has received a profit that is equal to the previous year's capital. How much profit will the Zvezda company receive at the end of 2003 if profits were not withdrawn from circulation?
Capital of the Zvezda company in 2000.
- capital of the Zvezda company in 2001.
- capital of the Zvezda company in 2002.
- capital of the Zvezda company in 2003.
Or we can write briefly:
For our case:
2000, 2001, 2002 and 2003.
Respectively:
rubles
Please note that in this problem we do not have a division either by or by, since the percentage is given ANNUALLY and it is calculated ANNUALLY. That is, when reading a problem on compound interest, pay attention to what percentage is given and in what period it is calculated, and only then proceed to calculations.
Now you know everything about geometric progression.
Training.
- Find the term of the geometric progression if it is known that, and
- Find the sum of the first terms of the geometric progression if it is known that, and
- The MDM Capital company began investing in the industry in 2003, with capital in dollars. Every year since 2004, it has received a profit that is equal to the previous year's capital. The MSK Cash Flows company began investing in the industry in 2005 in the amount of $10,000, starting to make a profit in 2006 in the amount of. By how many dollars is the capital of one company greater than the other at the end of 2007, if profits were not withdrawn from circulation?
Answers:
- Since the problem statement does not say that the progression is infinite and it is required to find the sum of a specific number of its terms, the calculation is carried out according to the formula:
MDM Capital Company:2003, 2004, 2005, 2006, 2007.
- increases by 100%, that is, 2 times.
Respectively:
rubles
MSK Cash Flows company:2005, 2006, 2007.
- increases by, that is, by times.
Respectively:
rubles
rubles
Let's summarize.
1) Geometric progression ( ) is a numerical sequence, the first term of which is different from zero, and each term, starting from the second, is equal to the previous one, multiplied by the same number. This number is called the denominator of a geometric progression.
2) The equation of the terms of the geometric progression is .
3) can take any values except and.
- if, then all subsequent terms of the progression have the same sign - they are positive;
- if, then all subsequent terms of the progression alternate signs;
- when – the progression is called infinitely decreasing.
4) , at – property of geometric progression (adjacent terms)
or
, at (equidistant terms)
When you find it, don’t forget that there should be two answers.
For example,
5) The sum of the terms of the geometric progression is calculated by the formula:
or
or
IMPORTANT! We use the formula for the sum of terms of an infinitely decreasing geometric progression only if the condition explicitly states that we need to find the sum of an infinite number of terms.
6) Problems on compound interest are also calculated using the formula of the th term of a geometric progression, provided that funds have not been withdrawn from circulation:
GEOMETRIC PROGRESSION. BRIEFLY ABOUT THE MAIN THINGS
Geometric progression( ) is a numerical sequence, the first term of which is different from zero, and each term, starting from the second, is equal to the previous one, multiplied by the same number. This number is called denominator of a geometric progression.
Denominator of geometric progression can take any value except and.
- If, then all subsequent terms of the progression have the same sign - they are positive;
- if, then all subsequent members of the progression alternate signs;
- when – the progression is called infinitely decreasing.
Equation of terms of geometric progression - .
Sum of terms of a geometric progression calculated by the formula:
or
If the progression is infinitely decreasing, then:
THE REMAINING 2/3 ARTICLES ARE AVAILABLE ONLY TO YOUCLEVER STUDENTS!
Become a YouClever student,
Prepare for the Unified State Exam or Unified State Exam in mathematics for the price of “a cup of coffee per month”,
And also get unlimited access to the “YouClever” textbook, the “100gia” preparation program (solver book), an unlimited trial Unified State Exam and Unified State Exam, 6000 problems with analysis of solutions, and other YouClever and 100gia services.
This number is called the denominator of a geometric progression, i.e. each term differs from the previous one by q times. (We will assume that q ≠ 1, otherwise everything is too trivial). It is easy to see that the general formula for the nth term of the geometric progression is b n = b 1 q n – 1 ; terms with numbers b n and b m differ by q n – m times.Already in Ancient Egypt they knew not only arithmetic, but also geometric progression. Here, for example, is a problem from the Rhind papyrus: “Seven faces have seven cats; Each cat eats seven mice, each mouse eats seven ears of corn, and each ear of barley can grow seven measures of barley. How large are the numbers in this series and their sum?
 |
|
Rice. 1. Ancient Egyptian geometric progression problem |
This task was repeated many times with different variations among other peoples at other times. For example, in written in the 13th century. “The Book of the Abacus” by Leonardo of Pisa (Fibonacci) has a problem in which 7 old women appear on their way to Rome (obviously pilgrims), each of whom has 7 mules, each of which has 7 bags, each of which contains 7 loaves , each of which has 7 knives, each of which has 7 sheaths. The problem asks how many objects there are.
The sum of the first n terms of the geometric progression S n = b 1 (q n – 1) / (q – 1) . This formula can be proven, for example, like this: S n = b 1 + b 1 q + b 1 q 2 + b 1 q 3 + ... + b 1 q n – 1.
Add the number b 1 q n to S n and get:
|
From here S n (q – 1) = b 1 (q n – 1), and we get the necessary formula.
Already on one of the clay tablets of Ancient Babylon, dating back to the 6th century. BC e., contains the sum 1 + 2 + 2 2 + 2 3 + ... + 2 9 = 2 10 – 1. True, as in a number of other cases, we do not know how this fact was known to the Babylonians.
The rapid increase in geometric progression in a number of cultures, in particular in Indian, is repeatedly used as a visual symbol of the vastness of the universe. In the famous legend about the appearance of chess, the ruler gives its inventor the opportunity to choose the reward himself, and he asks for the number of wheat grains that will be obtained if one is placed on the first square of the chessboard, two on the second, four on the third, eight on the fourth, and etc., each time the number doubles. Vladyka thought that at most we were talking about a few bags, but he miscalculated. It is easy to see that for all 64 squares of the chessboard the inventor would have to receive (2 64 - 1) grains, which is expressed as a 20-digit number; even if the entire surface of the Earth was sown, it would take at least 8 years to collect the required amount of grains. This legend is sometimes interpreted as indicating the virtually unlimited possibilities hidden in the game of chess.
It is easy to see that this number is really 20-digit:
2 64 = 2 4 ∙ (2 10) 6 = 16 ∙ 1024 6 ≈ 16 ∙ 1000 6 = 1.6∙10 19 (a more accurate calculation gives 1.84∙10 19). But I wonder if you can find out what digit this number ends with?
A geometric progression can be increasing if the denominator is greater than 1, or decreasing if it is less than one. In the latter case, the number q n for sufficiently large n can become arbitrarily small. While the increasing geometric progression increases unexpectedly quickly, the decreasing geometric progression decreases just as quickly.
The larger n, the weaker the number q n differs from zero, and the closer the sum of n terms of the geometric progression S n = b 1 (1 – q n) / (1 – q) to the number S = b 1 / (1 – q). (For example, F. Viet reasoned this way). The number S is called the sum of an infinitely decreasing geometric progression. However, for many centuries the question of what is the meaning of summing the ENTIRE geometric progression, with its infinite number of terms, was not clear enough to mathematicians.
A decreasing geometric progression can be seen, for example, in Zeno’s aporias “Half Division” and “Achilles and the Tortoise.” In the first case, it is clearly shown that the entire road (assuming length 1) is the sum of an infinite number of segments 1/2, 1/4, 1/8, etc. This is, of course, the case from the point of view of ideas about a finite sum infinite geometric progression. And yet - how can this be?
|
Rice. 2. Progression with a coefficient of 1/2 |
In the aporia about Achilles, the situation is a little more complicated, because here the denominator of the progression is not 1/2, but some other number. Let, for example, Achilles run with speed v, the tortoise moves with speed u, and the initial distance between them is l. Achilles will cover this distance in time l/v, and during this time the turtle will move a distance lu/v. When Achilles runs through this segment, the distance between him and the turtle will become equal to l (u /v) 2, etc. It turns out that catching up with the turtle means finding the sum of an infinitely decreasing geometric progression with the first term l and the denominator u /v. This sum - the segment that Achilles will eventually run to the meeting place with the turtle - is equal to l / (1 – u /v) = lv / (v – u). But, again, how this result should be interpreted and why it makes any sense at all was not very clear for a long time.
|
Rice. 3. Geometric progression with a coefficient of 2/3 |
Archimedes used the sum of a geometric progression to determine the area of a parabola segment. Let this segment of the parabola be delimited by the chord AB and let the tangent at point D of the parabola be parallel to AB. Let C be the midpoint of AB, E the midpoint of AC, F the midpoint of CB. Let's draw lines parallel to DC through points A, E, F, B; Let the tangent drawn at point D intersect these lines at points K, L, M, N. Let's also draw segments AD and DB. Let the line EL intersect the line AD at point G, and the parabola at point H; line FM intersects line DB at point Q, and the parabola at point R. According to the general theory of conic sections, DC is the diameter of a parabola (that is, a segment parallel to its axis); it and the tangent at point D can serve as coordinate axes x and y, in which the equation of the parabola is written as y 2 = 2px (x is the distance from D to any point of a given diameter, y is the length of a segment parallel to a given tangent from this point of diameter to some point on the parabola itself).
By virtue of the parabola equation, DL 2 = 2 ∙ p ∙ LH, DK 2 = 2 ∙ p ∙ KA, and since DK = 2DL, then KA = 4LH. Because KA = 2LG, LH = HG. The area of segment ADB of a parabola is equal to the area of triangle ΔADB and the areas of segments AHD and DRB combined. In turn, the area of the segment AHD is similarly equal to the area of the triangle AHD and the remaining segments AH and HD, with each of which you can perform the same operation - split into a triangle (Δ) and the two remaining segments (), etc.:
The area of the triangle ΔAHD is equal to half the area of the triangle ΔALD (they have a common base AD, and the heights differ by 2 times), which, in turn, is equal to half the area of the triangle ΔAKD, and therefore half the area of the triangle ΔACD. Thus, the area of the triangle ΔAHD is equal to a quarter of the area of the triangle ΔACD. Likewise, the area of triangle ΔDRB is equal to one-quarter of the area of triangle ΔDFB. So, the areas of the triangles ΔAHD and ΔDRB, taken together, are equal to a quarter of the area of the triangle ΔADB. Repeating this operation when applied to segments AH, HD, DR and RB will select triangles from them, the area of which, taken together, will be 4 times less than the area of triangles ΔAHD and ΔDRB, taken together, and therefore 16 times less, than the area of the triangle ΔADB. And so on:
Thus, Archimedes proved that “every segment contained between a straight line and a parabola constitutes four-thirds of a triangle having the same base and equal height.”
Lesson and presentation on the topic: "Number sequences. Geometric progression"
Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.
Educational aids and simulators in the Integral online store for grade 9
Powers and roots Functions and graphs
Guys, today we will get acquainted with another type of progression.
The topic of today's lesson is geometric progression.
Geometric progression
Definition. A numerical sequence in which each term, starting from the second, is equal to the product of the previous one and some fixed number is called a geometric progression.Let's define our sequence recursively: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
where b and q are certain given numbers. The number q is called the denominator of the progression.
Example. 1,2,4,8,16... A geometric progression in which the first term is equal to one, and $q=2$.
Example. 8,8,8,8... A geometric progression in which the first term is equal to eight,
and $q=1$.
Example. 3,-3,3,-3,3... Geometric progression in which the first term is equal to three,
and $q=-1$.
Geometric progression has the properties of monotony.
If $b_(1)>0$, $q>1$,
then the sequence is increasing.
If $b_(1)>0$, $0 The sequence is usually denoted in the form: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
Just like in an arithmetic progression, if in a geometric progression the number of elements is finite, then the progression is called a finite geometric progression.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Note that if a sequence is a geometric progression, then the sequence of squares of terms is also a geometric progression. In the second sequence, the first term is equal to $b_(1)^2$, and the denominator is equal to $q^2$.
Formula for the nth term of a geometric progression
Geometric progression can also be specified in analytical form. Let's see how to do this:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
We easily notice the pattern: $b_(n)=b_(1)*q^(n-1)$.
Our formula is called the "formula of the nth term of a geometric progression."
Let's return to our examples.
Example. 1,2,4,8,16... Geometric progression in which the first term is equal to one,
and $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Example. 16,8,4,2,1,1/2… A geometric progression in which the first term is equal to sixteen, and $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Example. 8,8,8,8... A geometric progression in which the first term is equal to eight, and $q=1$.
$b_(n)=8*1^(n-1)=8$.
Example. 3,-3,3,-3,3... A geometric progression in which the first term is equal to three, and $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Example. Given a geometric progression $b_(1), b_(2), …, b_(n), … $.
a) It is known that $b_(1)=6, q=3$. Find $b_(5)$.
b) It is known that $b_(1)=6, q=2, b_(n)=768$. Find n.
c) It is known that $q=-2, b_(6)=96$. Find $b_(1)$.
d) It is known that $b_(1)=-2, b_(12)=4096$. Find q.
Solution.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$, since $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Example. The difference between the seventh and fifth terms of the geometric progression is 192, the sum of the fifth and sixth terms of the progression is 192. Find the tenth term of this progression.
Solution.
We know that: $b_(7)-b_(5)=192$ and $b_(5)+b_(6)=192$.
We also know: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Then:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
We received a system of equations:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Equating our equations we get:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
We got two solutions q: $q_(1)=2, q_(2)=-1$.
Substitute sequentially into the second equation:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ no solutions.
We got that: $b_(1)=4, q=2$.
Let's find the tenth term: $b_(10)=b_(1)*q^9=4*2^9=2048$.
Sum of a finite geometric progression
Let us have a finite geometric progression. Let's, just like for an arithmetic progression, calculate the sum of its terms.Let a finite geometric progression be given: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Let us introduce the designation for the sum of its terms: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
In the case when $q=1$. All terms of the geometric progression are equal to the first term, then it is obvious that $S_(n)=n*b_(1)$.
Let us now consider the case $q≠1$.
Let's multiply the above amount by q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Note:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2 )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
We have obtained the formula for the sum of a finite geometric progression.
Example.
Find the sum of the first seven terms of a geometric progression whose first term is 4 and the denominator is 3.
Solution.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Example.
Find the fifth term of the geometric progression that is known: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Solution.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q=$1364.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Characteristic property of geometric progression
Guys, a geometric progression is given. Let's look at its three consecutive members: $b_(n-1),b_(n),b_(n+1)$.We know that:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Then:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
If the progression is finite, then this equality holds for all terms except the first and last.
If it is not known in advance what form the sequence has, but it is known that: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Then we can safely say that this is a geometric progression.
A number sequence is a geometric progression only when the square of each member is equal to the product of the two adjacent members of the progression. Do not forget that for a finite progression this condition is not satisfied for the first and last terms.
Let's look at this identity: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ is called the geometric mean of the numbers a and b.
The modulus of any term of a geometric progression is equal to the geometric mean of its two adjacent terms.
Example.
Find x such that $x+2; 2x+2; 3x+3$ were three consecutive terms of a geometric progression.
Solution.
Let's use the characteristic property:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ and $x_(2)=-1$.
Let us sequentially substitute our solutions into the original expression:
With $x=2$, we got the sequence: 4;6;9 – a geometric progression with $q=1.5$.
For $x=-1$, we get the sequence: 1;0;0.
Answer: $x=2.$
Problems to solve independently
1. Find the eighth first term of the geometric progression 16;-8;4;-2….2. Find the tenth term of the geometric progression 11,22,44….
3. It is known that $b_(1)=5, q=3$. Find $b_(7)$.
4. It is known that $b_(1)=8, q=-2, b_(n)=512$. Find n.
5. Find the sum of the first 11 terms of the geometric progression 3;12;48….
6. Find x such that $3x+4; 2x+4; x+5$ are three consecutive terms of a geometric progression.
Anna Malkova
Geometric progression is a sequence, each term of which, starting from the second, is equal to the product of the previous term and some fixed number q:
Fixed number q called the denominator of a geometric progression.
Formula for the nth term of a geometric progression:
Formula for the sum of the first members of the geometric progression is calculated by the formula:
The square of each term of the geometric progression, starting from the second, is equal to the product of the neighboring ones:
1. Algae grows on the surface of the lake. Within a day, each algae is divided in half, and instead of one algae, two appear. After another day, each of the resulting algae is divided in half and so on. After 30 days, the lake was completely covered with algae. How long did it take for the lake to be half full?
The answer is paradoxical: after 29 days.
This problem is best solved “from the end”. Here in front of you is a lake filled with algae. What happened a day ago? Obviously, there were half as many algae, that is, the lake was half covered with them.
Every day there was twice as much algae in the lake, that is, their number increased in geometric progression.
2. Unified State Exam) Businessman Bublikov received a profit of 5,000 rubles in 2000. Each subsequent year, his profits increased by 300% compared to the previous year. How many rubles did Bublikov earn in 2003?
Bublikov’s profit in 2000 was small. But every year the profit increased by 300%, that is, 4 times compared to the previous year. Geometric progression! We are looking for her fourth member:
3. (Unified State Examination Problem) The Alpha company began investing in a promising industry in 2001, with a capital of $3,000. Every year since 2002, it has made a profit that was 100% of the previous year's capital. And Beta Company began investing in another industry in 2003 with $6,000 in capital and, since 2004, has made an annual profit of 200% of the previous year's capital. By how many dollars was the capital of one company greater than the capital of the other at the end of 2006, if profits were not withdrawn from circulation?
Let us define the basic concepts of the problem.
Company capital– the totality of all funds available to the company.
Profit– the difference between income and expenses (costs).
If in 2002 the profit of the Alpha company is 100% of the capital of the previous year, it means that the capital of the Alpha company has doubled over the year. Likewise, Alpha's capital doubles in 2003, 2004, 2005 and 2006, meaning it was thousands of dollars in 2006.
The capital of the Beta company increases 3 times annually. In 2006, it increased several times compared to 2003 and amounted to dollars.
This is 66 thousand dollars more than the capital of the Alpha company.
Infinitely decreasing geometric progression
A geometric progression whose denominator is |q|<1, называется бесконечно убывающей.
An example of an infinitely decreasing geometric progression.
What is its amount?

Let's draw a rectangle with area 1. Add to it areas with area
What does the area of the resulting figure tend to with an infinite increase in n, that is, with the addition of ever smaller areas? Obviously, by two.
The sum of an infinitely decreasing geometric progression is a number that is found by the formula:
There is a mathematical joke, and now you will understand it.
An infinite number of mathematicians walk into a bar. The first one says: “I’ll have a glass of beer!” Second: “I’ll have half a glass of beer!” Third: “I’ll have a quarter of a glass of beer!” Fourth: “I’ll have a glass of beer!” Bartender: “Wait a minute... I know your tricks - you have two glasses of beer for everyone!”
Unified State Exam problems for independent solution
1. Businessman Korovin received a profit of 1,400,000 rubles in 2000. Each subsequent year, his profits increased by 20% compared to the previous year. How many rubles did Korovin make in 2004?
2. Alpha Company began investing in a promising industry in 2001 with a capital of $4,000. Every year since 2002, it has made a profit that was 100% of the previous year's capital. And Beta Company began investing in another industry in 2004 with $4,500 in capital and, since 2005, has made an annual profit of 200% of the previous year's capital. By how many dollars was the capital of one company greater than the capital of the other at the end of 2007, if profits were not withdrawn from circulation?
- Answer: 2 903 040
- Answer: 134500
Lesson on the topic “Infinitely decreasing geometric progression”
The purpose of the lesson: introducing students to a new type of sequence - an infinitely decreasing geometric progression.
Tasks:
formulating an initial idea of the limit of a numerical sequence; acquaintance with another way to convert infinite periodic fractions into ordinary ones using the formula for the sum of an infinitely decreasing geometric progression;
development of intellectual qualities of schoolchildren’s personality such as logical thinking, ability to make evaluative actions, and generalization;
fostering activity, mutual assistance, collectivism, and interest in the subject.
Equipment: computer class, projector, screen.
Lesson type: lesson - learning a new topic.
During the classes
I . Org. moment. State the topic and purpose of the lesson.
II . Updating students' knowledge.1. Checking homework.
1) Checking basic formulas related to arithmetic and geometric progressions. Two students are preparing notes on formulas at the blackboard.
2) The rest of the students do mathematical dictation on the topic “Sum Formulas”.
Tasks:
№1. Find the sum of the first five terms of an arithmetic progression if its first term is 6 (1st option), -20 (2nd option), and the fifth term is -6 (1st option), 20 (2nd option).
№2. Find the sum of the first five terms of an arithmetic progression if its first term is -20 (1st option), 6 (2nd option), and the difference is 10 (1st option), -3 (2nd option).
№3. Find the sum of the first five terms of a geometric progression if its first term is equal to 1 (1st option), -1 (2nd option), and the denominator is -2 (1st option), 2 (2nd option).
At the end of the dictation, two students’ work is selectively checked for assessment, the rest perform a self-test using ready-made solutions written on the flaps of the board.
Solutions:

Tasks
1. Arithmetic progression is given by the formula a n = 7 – 4 n. Find a 10 . (-33)
2. In arithmetic progression a 3 = 7 And a 5 = 1 . Find a 4 . (4)
3. In arithmetic progression a 3 = 7 And a 5 = 1 . Find a 17 . (-35)
4. In arithmetic progression a 3 = 7 And a 5 = 1 . Find S 17 . (-187)
5. For geometric progression  find the fifth term.
find the fifth term. 
6. For geometric progression  find n th member.
find n th member. 
7. Exponentially b 3 = 8 And b 5 = 2 . Find b 4 . (4)
8. Exponentially b
3
= 8
And b
5
= 2
. Find b
1
And
q
. 
9. Exponentially b 3 = 8 And b 5 = 2 . Find S 5 . (62)
III . Learning a new topic(demonstration of presentation).

Consider a square with a side equal to 1. Let's draw another square whose side is half the size of the first square, then another one whose side is half the second, then the next one, etc. Each time the side of the new square is equal to half of the previous one.
As a result, we received a sequence of sides of squares  forming a geometric progression with the denominator .
forming a geometric progression with the denominator .
And, what is very important, the more we build such squares, the smaller the side of the square will be. For example,

Those. As the number n increases, the terms of the progression approach zero.
Using this figure, you can consider another sequence.

For example, the sequence of areas of squares:

 . And, again, if n increases indefinitely, then the area approaches zero as close as you like.
. And, again, if n increases indefinitely, then the area approaches zero as close as you like.
Let's look at another example. An equilateral triangle with sides equal to 1 cm. Let's construct the following triangle with the vertices in the midpoints of the sides of the 1st triangle, according to the theorem about the midline of the triangle - the side of the 2nd is equal to half the side of the first, the side of the 3rd is equal to half the side of the 2nd, etc. Again we obtain a sequence of lengths of the sides of triangles.
 at
at  .
.
If we consider a geometric progression with a negative denominator.
Then, again, with increasing numbers n terms of the progression approach zero.
Let's pay attention to the denominators of these sequences. Everywhere the denominators were less than 1 in absolute value.
We can conclude: a geometric progression will be infinitely decreasing if the modulus of its denominator is less than 1.
Frontal work.
Definition:
A geometric progression is said to be infinitely decreasing if the modulus of its denominator is less than one.  .
.
Using the definition, you can decide whether a geometric progression is infinitely decreasing or not.
Task
Is the sequence an infinitely decreasing geometric progression if it is given by the formula:
 ;
;  .
.
Solution:
 . We'll find q
.
. We'll find q
.
 ;
;  ;
;  ;
;  .
.
this geometric progression is infinitely decreasing.
b) this sequence is not an infinitely decreasing geometric progression.

Consider a square with a side equal to 1. Divide it in half, one of the halves in half, etc. The areas of all the resulting rectangles form an infinitely decreasing geometric progression: ![]()
The sum of the areas of all rectangles obtained in this way will be equal to the area of the 1st square and equal to 1. ![]()
But on the left side of this equality is the sum of an infinite number of terms.
Let's consider the sum of the first n terms. ![]()
According to the formula for the sum of the first n terms of a geometric progression, it is equal to  .
.
If n increases without limit, then
or  . That's why
. That's why  , i.e.
, i.e.  .
.
Sum of an infinitely decreasing geometric progression there is a sequence limit S 1 , S 2 , S 3 , …, S n , … .
For example, for progression  ,
,
 Because
Because 
The sum of an infinitely decreasing geometric progression can be found using the formula 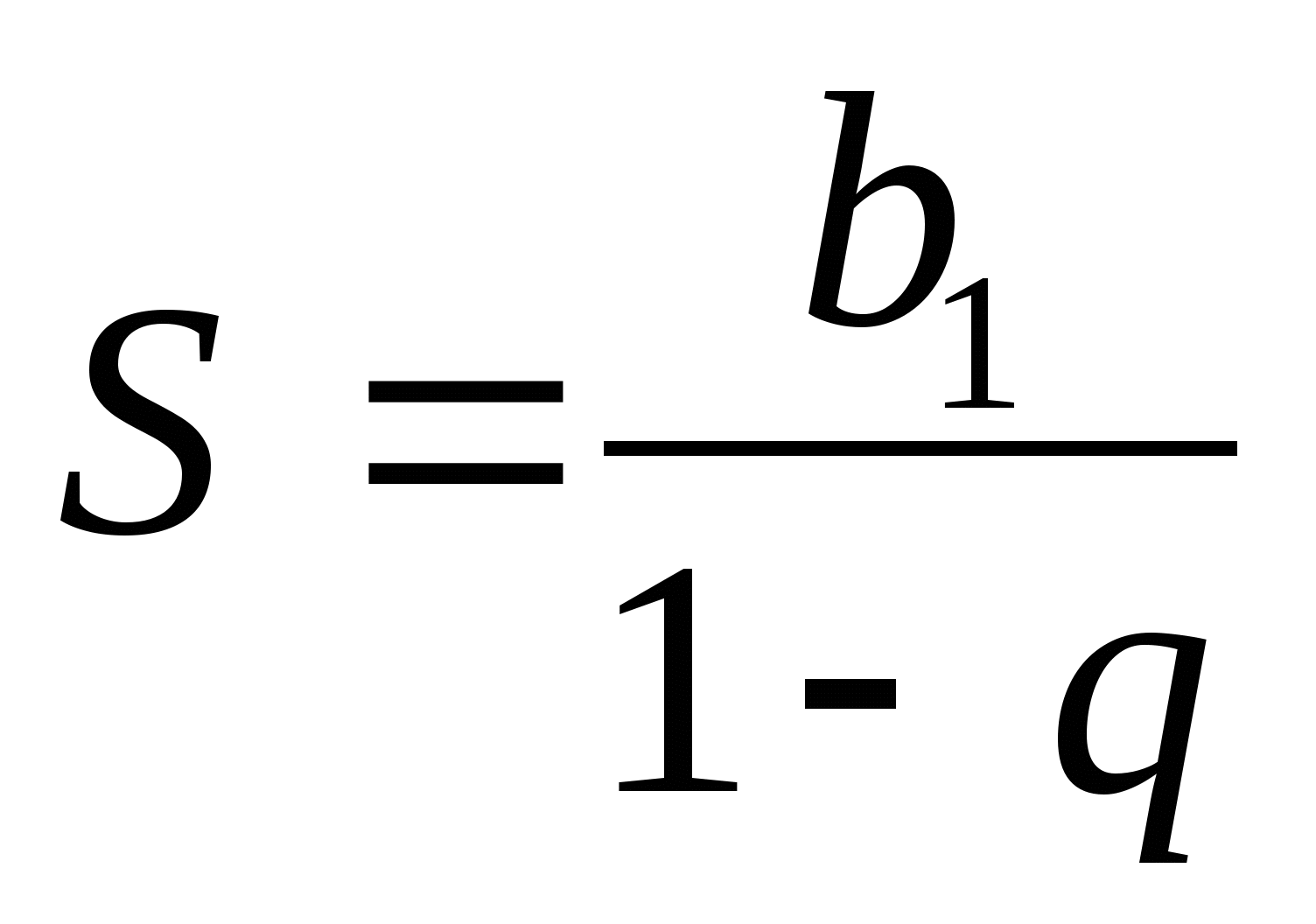 .
.
III . Comprehension and consolidation(completing tasks).
Task No. 2. Find the sum of an infinitely decreasing geometric progression with the first term being 3 and the second term being 0.3.
Solution:
Task No. 3. textbook, p. 160, No. 433(1)
Find the sum of an infinitely decreasing geometric progression:
Solution:

Task No. 4. Write the infinite periodic decimal fraction 0,(5) as a common fraction.
1st method. Let x=0,(5)= 0.555... / 10 2nd method. 0,(5)=0.555…=

Task No. 5. textbook, p. 162, No. 445(3) (independent solution)
Write the infinite periodic decimal fraction 0,(12) as a common fraction.
Answer: 0,(12)= 4/33.
IV . Summarizing.
What sequence did you get acquainted with today?
Define an infinitely decreasing geometric progression.
How to prove that a geometric progression is infinitely decreasing?
Give the formula for the sum of an infinitely decreasing geometric progression.
V . Homework.
