WAVE INTERFERENCE(from Latin inter - mutually, between each other and ferio - I strike, I strike) - mutual strengthening or weakening of two (or more) waves when they are superimposed on each other at the same time. distribution in space. Usually under . The effect refers to the difference between the resulting intensity of the wave field and the sum of the intensities of the initial waves. I.v. is one of the main. properties of waves of any nature (elastic, el-magnetic, including light, etc.), and such characteristic wave phenomena as propagation and are also associated with interference. Calculation of I.v. in linear environments is based on superposition principle, according to Krom, the resulting wave field created by several. sources, is equal to the sum of the fields from the individual components. For sinusoidal (harmonic) waves in time, it is convenient to use the formalism of complex amplitudes: , where A and j are the real amplitude and phase of the wave. According to the principle of superposition, the complex amplitude of the resulting field is simply equal to the sum of those of the separate field. terms (), and for the intensity of wave A 2 in the case of two waves with amplitudes 
we have A 2 =A 2 1 +A 2 2 +2A 1 A 2 сosDj, (1) where Dj=j 2 -j 1 . Quantities A 1,2, j 1,2 in (1) in the general case are certain functions of coordinates and time, the type of which is determined by the specific structure of the interfering wills (for example, they depend on the distance to the corresponding sources and their phases) . As a result, at those points where Dj=m.2p, where m=0, b1, b2, . . ., A = A 1 + A 2 , and the intensity of A 2 takes on a maximum value that exceeds the sum of the intensities of the superimposed waves. At points where Dj=(m+ 1 / 2)2p, interference occurs. minimum: A=|A 1 - A 2 |. In a special case A 1 =A 2 at these points the total amplitude is zero, in other words, the interfering waves completely “quench” each other. In three-dimensional space geom. places of points of maxima and minima corresponding to the definition. "orders" m, are certain surfaces, the intersection of which with an arbitrary plane of observation (screen) gives the so-called. interference stripes. For example, in the case of two plane waves with phases j 1 = -k 1 r+j 0 1, j 2 = -k 2 r+j 02 (where k 1.2 -, j 01, j 02 - initial phases, determined sources, k 1 =k 2 =2p/l) we have: Dj=-Dkr+j 02 -j 0 1 . where Dk=k 2 -k 1 and the surfaces of maxima and minima will be planes perpendicular to the vector Dk; in this case, the distance between adjacent maxima is equal to l -1, where l is the wavelength, a=|Dk|/k is the angle between the vectors k 1 and k 2. Limiting case a=p and A 1 =A 2 matches standing wave, it can be implemented, for example, with full reflection running from a certain plane perpendicular to the direction of its propagation.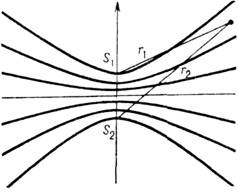 
Rice. 1. Wave interference from two point sources. Dr. typical example- interference of two spherical waves emanating from the corresponding centers S 1 and S 2 (Fig. 1), spaced at a certain distance d=S 1 S 2. In this case, Dj=-kD+j 02 -j 01 (where D=r 2 -r 1 is the path difference, r 1.2 is the distance from the sources to the observation point) and the maxima, as well as the minima between them, are located on hyperboloids of rotation around the S 1 axis S 2, and in a plane parallel to this axis there is interference. the stripes look like hyperbolas. Total number maxima here is determined from the condition |m|,"de":["H-899KMDjv4","j13vBH-qns4","j13vBH-qns4"],"es":["jPHPvIjlqxA","H02ZBgrzkNU","jPHPvIjlqxA", "jPHPvIjlqxA","z16BTcIRilE"],"pt":["LWTlwfey3MA","H02ZBgrzkNU","dqD_gN0yv3w"],"fr":["3tf5ZV3lLKc","J_xd9hUZ2AY"],"pl":["e9qPtS9jZH4", "4H90aA5aYMw"],"ro":["vG2lXZ4500c"],"la":["OlJ6dS3S104","21O4a5KFtkM","OlJ6dS3S104","21O4a5KFtkM"])
