Decimal. The whole part. Decimal point.
Decimal places. Properties of decimal fractions.
Periodic decimal fraction. Period .
Decimal is the result of dividing one by ten, one hundred, thousand, etc. parts. These fractions are very convenient for calculations, since they are based on the same positional system on which counting and writing integers are based. Thanks to this, the notation and rules for working with decimal fractions are essentially the same as for whole numbers. When writing decimal fractions, there is no need to mark the denominator; this is determined by the place occupied by the corresponding digit. First it is written whole part numbers, then put on the right decimal point. The first digit after the decimal point means the number of tenths, the second – the number of hundredths, the third – the number of thousandths, etc. The numbers located after the decimal point are called decimals.
EXAMPLE
One of advantages of decimals– they are easy brought to mindordinary: the number after the decimal point (in our case 5047) is the numerator; the denominator is equaln-th power of 10, wheren- number of decimal places(in our case n= 4):
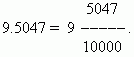
If a decimal fraction does not contain an integer part, then a zero is placed before the decimal point:
Properties of decimal fractions.
1. The decimal does not change if you add zeros to the right:
13.6 =13.6000.
2. The decimal fraction does not change if you remove the zeros located
at the end decimal:
0.00123000 = 0.00123 .
Attention! You cannot remove non-terminal zeros. decimal!
These properties allow you to quickly multiply and divide decimals by 10, 100, 1000, etc.
Periodic decimal contains an infinitely repeating group of numbers called period. The period is written in parentheses. For example, 0.12345123451234512345… = 0.(12345).
EXAMPLE If we divide 47 by 11, we get 4.27272727… = 4.(27).
To write a rational number m/n as a decimal fraction, you need to divide the numerator by the denominator. In this case, the quotient is written as a finite or infinite decimal fraction.
Write this number as a decimal fraction.
Solution. Divide the numerator of each fraction into a column by its denominator: A) divide 6 by 25; b) divide 2 by 3; V) divide 1 by 2, and then add the resulting fraction to one - the integer part of this mixed number.

Irreducible ordinary fractions whose denominators do not contain prime factors other than 2 And 5 , are written as a final decimal fraction.
IN example 1 in case A) denominator 25=5·5; in case V) the denominator is 2, so we get the final decimals 0.24 and 1.5. In case b) the denominator is 3, so the result cannot be written as a finite decimal.
Is it possible, without long division, to convert into a decimal fraction such an ordinary fraction, the denominator of which does not contain other divisors other than 2 and 5? Let's figure it out! What fraction is called a decimal and is written without a fraction bar? Answer: fraction with denominator 10; 100; 1000, etc. And each of these numbers is a product equal number of twos and fives. In fact: 10=2 ·5 ; 100=2 ·5 ·2 ·5 ; 1000=2 ·5 ·2 ·5 ·2 ·5 etc.
Consequently, the denominator of an irreducible ordinary fraction will need to be represented as the product of “twos” and “fives”, and then multiplied by 2 and (or) 5 so that the “twos” and “fives” become equal. Then the denominator of the fraction will be equal to 10 or 100 or 1000, etc. To ensure that the value of the fraction does not change, we multiply the numerator of the fraction by the same number by which we multiplied the denominator.
Express the following common fractions as decimals:
![]()
Solution. Each of these fractions is irreducible. Let's factor the denominator of each fraction into prime factors.
20=2·2·5. Conclusion: one “A” is missing.
8=2·2·2. Conclusion: three “A”s are missing.
25=5·5. Conclusion: two “twos” are missing.

Comment. In practice, they often do not use factorization of the denominator, but simply ask the question: by how much should the denominator be multiplied so that the result is one with zeros (10 or 100 or 1000, etc.). And then the numerator is multiplied by the same number.
So, in case A)(example 2) from the number 20 you can get 100 by multiplying by 5, therefore, you need to multiply the numerator and denominator by 5.
In case b)(example 2) from the number 8 the number 100 will not be obtained, but the number 1000 will be obtained by multiplying by 125. Both the numerator (3) and the denominator (8) of the fraction are multiplied by 125.
In case V)(example 2) from 25 you get 100 if you multiply by 4. This means that the numerator 8 must be multiplied by 4.
An infinite decimal fraction in which one or more digits invariably repeat in the same sequence is called periodic as a decimal. The set of repeating digits is called the period of this fraction. For brevity, the period of a fraction is written once, enclosed in parentheses.
In case b)(example 1) there is only one repeating digit and is equal to 6. Therefore, our result 0.66... will be written like this: 0,(6) . They read: zero point, six in period.
If there are one or more non-repeating digits between the decimal point and the first period, then such a periodic fraction is called a mixed periodic fraction.
An irreducible common fraction whose denominator is together with others multipliers contains a multiplier 2 or 5 , turns to mixed periodic fraction.
Write numbers as decimals.
Of the many fractions found in arithmetic, those that have 10, 100, 1000 in the denominator - in general, any power of ten - deserve special attention. These fractions have a special name and notation.
A decimal is any number fraction whose denominator is a power of ten.
Examples of decimal fractions:
Why was it necessary to separate out such fractions at all? Why do they need their own recording form? There are at least three reasons for this:
- Decimals are much easier to compare. Remember: to compare ordinary fractions, you need to subtract them from each other and, in particular, bring the fractions to a common denominator. In decimals nothing like this is required;
- Reduce computation. Decimals add and multiply according to their own rules, and with a little practice you'll be able to work with them much faster than with regular fractions;
- Ease of recording. Unlike ordinary fractions, decimals are written on one line without loss of clarity.
Most calculators also give answers in decimals. In some cases, a different recording format may cause problems. For example, what if you ask for change in the store in the amount of 2/3 of a ruble :)
Rules for writing decimal fractions
The main advantage of decimal fractions is convenient and visual notation. Namely:
Decimal notation is a form of writing decimal fractions where the integer part is separated from the fractional part by a regular period or comma. In this case, the separator itself (period or comma) is called a decimal point.
For example, 0.3 (read: “zero pointers, 3 tenths”); 7.25 (7 whole, 25 hundredths); 3.049 (3 whole, 49 thousandths). All examples are taken from the previous definition.
In writing, a comma is usually used as a decimal point. Here and further throughout the site, the comma will also be used.
To write an arbitrary decimal fraction in this form, you need to follow three simple steps:
- Write out the numerator separately;
- Shift the decimal point to the left by as many places as there are zeros in the denominator. Assume that initially the decimal point is to the right of all digits;
- If the decimal point has moved, and after it there are zeros at the end of the entry, they must be crossed out.
It happens that in the second step the numerator does not have enough digits to complete the shift. In this case, the missing positions are filled with zeros. And in general, to the left of any number you can assign any number of zeros without harm to your health. It's ugly, but sometimes useful.
At first glance, this algorithm may seem quite complicated. In fact, everything is very, very simple - you just need to practice a little. Take a look at the examples:
Task. For each fraction, indicate its decimal notation:
The numerator of the first fraction is: 73. We shift the decimal point by one sign (since the denominator is 10) - we get 7.3.
Numerator of the second fraction: 9. We shift the decimal point by two places (since the denominator is 100) - we get 0.09. I had to add one zero after the decimal point and one more before it, so as not to leave a strange entry like “.09”.
The numerator of the third fraction is: 10029. We shift the decimal point by three places (since the denominator is 1000) - we get 10.029.
The numerator of the last fraction: 10500. Again we shift the point by three digits - we get 10,500. There are extra zeros at the end of the number. Cross them out and we get 10.5.
Pay attention to the last two examples: the numbers 10.029 and 10.5. According to the rules, the zeros on the right must be crossed out, as was done in the last example. However, you should never do this with zeros inside a number (which are surrounded by other numbers). That's why we got 10.029 and 10.5, and not 1.29 and 1.5.
So, we figured out the definition and form of writing decimal fractions. Now let's find out how to convert ordinary fractions to decimals - and vice versa.
Conversion from fractions to decimals
Let's consider a simple numerical fraction of the form a /b. You can use the basic property of a fraction and multiply the numerator and denominator by such a number that the bottom turns out to be a power of ten. But before you do, read the following:
There are denominators that cannot be reduced to powers of ten. Learn to recognize such fractions, because they cannot be worked with using the algorithm described below.
That's how things are. Well, how do you understand whether the denominator is reduced to a power of ten or not?
The answer is simple: factor the denominator into prime factors. If the expansion contains only factors 2 and 5, this number can be reduced to a power of ten. If there are other numbers (3, 7, 11 - whatever), you can forget about the power of ten.
Task. Check whether the indicated fractions can be represented as decimals:
Let us write out and factor the denominators of these fractions:
20 = 4 · 5 = 2 2 · 5 - only the numbers 2 and 5 are present. Therefore, the fraction can be represented as a decimal.
12 = 4 · 3 = 2 2 · 3 - there is a “forbidden” factor 3. The fraction cannot be represented as a decimal.
640 = 8 · 8 · 10 = 2 3 · 2 3 · 2 · 5 = 2 7 · 5. Everything is in order: there is nothing except the numbers 2 and 5. A fraction can be represented as a decimal.
48 = 6 · 8 = 2 · 3 · 2 3 = 2 4 · 3. The factor 3 “surfaced” again. It cannot be represented as a decimal fraction.
So, we’ve sorted out the denominator - now let’s look at the entire algorithm for moving to decimal fractions:
- Factor the denominator of the original fraction and make sure that it is generally representable as a decimal. Those. check that only factors 2 and 5 are present in the expansion. Otherwise, the algorithm does not work;
- Count how many twos and fives are present in the expansion (there will be no other numbers there, remember?). Choose an additional factor such that the number of twos and fives is equal.
- Actually, multiply the numerator and denominator of the original fraction by this factor - we get the desired representation, i.e. the denominator will be a power of ten.
Of course, the additional factor will also be decomposed only into twos and fives. At the same time, in order not to complicate your life, you should choose the smallest multiplier of all possible ones.
And one more thing: if the original fraction contains an integer part, be sure to convert this fraction to an improper fraction - and only then apply the described algorithm.
Task. Convert these numerical fractions to decimals:
Let's factorize the denominator of the first fraction: 4 = 2 · 2 = 2 2 . Therefore, the fraction can be represented as a decimal. The expansion contains two twos and not a single five, so the additional factor is 5 2 = 25. With it, the number of twos and fives will be equal. We have:
Now let's look at the second fraction. To do this, note that 24 = 3 · 8 = 3 · 2 3 - there is a triple in the expansion, so the fraction cannot be represented as a decimal.
The last two fractions have denominators 5 (prime number) and 20 = 4 · 5 = 2 2 · 5 respectively - only twos and fives are present everywhere. Moreover, in the first case, “for complete happiness” a factor of 2 is not enough, and in the second - 5. We get:
Conversion from decimals to common fractions
The reverse conversion - from decimal to regular notation - is much simpler. There are no restrictions or special checks here, so you can always convert a decimal fraction to the classic “two-story” fraction.
The translation algorithm is as follows:
- Cross out all the zeros on the left side of the decimal, as well as the decimal point. This will be the numerator of the desired fraction. The main thing is not to overdo it and do not cross out the inner zeros surrounded by other numbers;
- Count how many decimal places there are after the decimal point. Take the number 1 and add as many zeros to the right as there are characters you count. This will be the denominator;
- Actually, write down the fraction whose numerator and denominator we just found. If possible, reduce it. If the original fraction contained an integer part, we will now get an improper fraction, which is very convenient for further calculations.
Task. Convert decimal fractions to ordinary fractions: 0.008; 3.107; 2.25; 7,2008.
Cross out the zeros on the left and the commas - we get the following numbers (these will be the numerators): 8; 3107; 225; 72008.
In the first and second fractions there are 3 decimal places, in the second - 2, and in the third - as many as 4 decimal places. We get the denominators: 1000; 1000; 100; 10000.
Finally, let's combine the numerators and denominators into ordinary fractions:

As can be seen from the examples, the resulting fraction can very often be reduced. Let me note once again that any decimal fraction can be represented as an ordinary fraction. The reverse conversion may not always be possible.
In this article we will understand what a decimal fraction is, what features and properties it has. Let's go! 🙂
A decimal fraction is a special case of ordinary fractions (where the denominator is a multiple of 10).
Definition
Decimals are fractions whose denominators are numbers consisting of one and a number of zeros following it. That is, these are fractions with a denominator of 10, 100, 1000, etc. Otherwise, a decimal fraction can be characterized as a fraction with a denominator of 10 or one of the powers of ten.
Examples of fractions:
, ,
Decimal fractions are written differently than ordinary fractions. Operations with these fractions are also different from operations with ordinary ones. The rules for operations with them are largely similar to the rules for operations with integers. This, in particular, explains their demand for solving practical problems.
Representation of fractions in decimal notation
The decimal fraction does not have a denominator; it displays the number of the numerator. In general, a decimal fraction is written according to the following scheme:
where X is the integer part of the fraction, Y is its fractional part, “,” is the decimal point.
To correctly represent a fraction as a decimal, it must be a proper fraction, that is, with the integer part highlighted (if possible) and a numerator that is less than the denominator. Then in decimal notation the integer part is written before the decimal point (X), and the numerator of the common fraction is written after the decimal point (Y).
If the numerator contains a number with fewer digits than the number of zeros in the denominator, then in part Y the missing number of digits in the decimal notation is filled with zeros ahead of the numerator digits.
Example: ![]()
If a common fraction is less than 1, i.e. does not have an integer part, then for X in decimal form write 0.
In the fractional part (Y), after the last significant (non-zero) digit, an arbitrary number of zeros can be entered. This does not affect the value of the fraction. Conversely, all zeros at the end of the fractional part of the decimal can be omitted.
Reading Decimals
Part X is generally read as follows: “X integers.”
The Y part is read according to the number in the denominator. For denominator 10 you should read: “Y tenths”, for denominator 100: “Y hundredths”, for denominator 1000: “Y thousandths” and so on... 😉
Another approach to reading, based on counting the number of digits of the fractional part, is considered more correct. To do this, you need to understand that the fractional digits are located in a mirror image with respect to the digits of the whole part of the fraction.
The names for correct reading are given in the table:

Based on this, reading should be based on compliance with the name of the digit of the last digit of the fractional part.
- 3.5 reads "three point five"
- 0.016 reads "zero point sixteen thousandths"
Converting an arbitrary fraction to a decimal
If the denominator of a common fraction is 10 or some power of ten, then the conversion of the fraction is performed as described above. In other situations, additional transformations are required.
There are 2 translation methods.
First transfer method
The numerator and denominator must be multiplied by such an integer that the denominator produces the number 10 or one of the powers of ten. And then the fraction is represented in decimal notation.
This method is applicable for fractions whose denominator can only be expanded into 2 and 5. So, in the previous example ![]() . If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
. If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
Second translation method
The 2nd method is to divide the numerator by the denominator in a column or on a calculator. The whole part, if any, does not participate in the transformation.
The rule for long division that results in a decimal fraction is described below (see Division of decimals).
Converting a decimal fraction to a common fraction
To do this, you should write its fractional part (to the right of the decimal point) as a numerator, and the result of reading the fractional part as the corresponding number in the denominator. Next, if possible, you need to reduce the resulting fraction.
![]()
Finite and infinite decimal fraction
A decimal fraction is called a final fraction, the fractional part of which consists of a finite number of digits.
All the examples above contain final decimal fractions. However, not every common fraction can be represented as a final decimal. If the 1st conversion method is not applicable for a given fraction, and the 2nd method demonstrates that the division cannot be completed, then only an infinite decimal fraction can be obtained.
It is impossible to write an infinite fraction in its complete form. In incomplete form, such fractions can be represented:
- as a result of reduction to the desired number of decimal places;
- as a periodic fraction.
A fraction is called periodic if after the decimal point it is possible to distinguish an endlessly repeating sequence of digits.
The remaining fractions are called non-periodic. For non-periodic fractions, only the 1st method of representation (rounding) is allowed.
An example of a periodic fraction: 0.8888888... Here there is a repeating number 8, which, obviously, will be repeated ad infinitum, since there is no reason to assume otherwise. This figure is called period of the fraction.
Periodic fractions can be pure or mixed. A pure decimal fraction is one whose period begins immediately after the decimal point. A mixed fraction has 1 or more digits before the decimal point.
54.33333… – periodic pure decimal fraction
2.5621212121… – periodic mixed fraction
Examples of writing infinite decimal fractions:
The 2nd example shows how to correctly format a period in writing a periodic fraction.
Converting periodic decimal fractions to ordinary fractions
To convert a pure periodic fraction into an ordinary period, write it into the numerator, and write a number consisting of nines in an amount equal to the number of digits in the period into the denominator.
![]()
The mixed periodic decimal fraction is translated as follows:
- you need to form a number consisting of the number after the decimal point before the period and the first period;
- From the resulting number, subtract the number after the decimal point before the period. The result will be the numerator of the common fraction;
- in the denominator you need to enter a number consisting of a number of nines equal to the number of digits of the period, followed by zeros, the number of which is equal to the number of digits of the number after the decimal point before the 1st period.
![]()
![]()
Comparison of decimals
Decimal fractions are compared initially by their whole parts. The fraction whose whole part is larger is greater.
If the integer parts are the same, then compare the digits of the corresponding digits of the fractional part, starting from the first (from the tenths). The same principle applies here: the larger fraction is the one with more tenths; if the tenths digits are equal, the hundredths digits are compared, and so on.
Since
![]() , since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger number of hundredths.
, since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger number of hundredths.
Adding and subtracting decimals
Decimals are added and subtracted in the same way as whole numbers by writing the corresponding digits below each other. To do this, you need to have decimal points below each other. Then the units (tens, etc.) of the integer part, as well as the tenths (hundredths, etc.) of the fractional part, will be in accordance. The missing digits of the fractional part are filled with zeros. Directly the process of addition and subtraction is carried out in the same way as for integers.
Multiplying Decimals
To multiply decimals, you need to write them one below the other, aligned with the last digit and not paying attention to the location of the decimal points. Then you need to multiply the numbers in the same way as when multiplying whole numbers. After receiving the result, you should recalculate the number of digits after the decimal point in both fractions and separate the total number of fractional digits in the resulting number with a comma. If there are not enough digits, they are replaced with zeros.

Multiplying and dividing decimals by 10n
These actions are simple and boil down to moving the decimal point. P When multiplying, the decimal point is moved to the right (the fraction is increased) by a number of digits equal to the number of zeros in 10n, where n is an arbitrary integer power. That is, a certain number of digits are transferred from the fractional part to the whole part. When dividing, accordingly, the comma is moved to the left (the number decreases), and some of the digits are transferred from the integer part to the fractional part. If there are not enough numbers to transfer, then the missing digits are filled with zeros.
Dividing a decimal and a whole number by a whole number and a decimal
Dividing a decimal by an integer is similar to dividing two integers. Additionally, you only need to take into account the position of the decimal point: when removing the digit of a place followed by a comma, you must place a comma after the current digit of the generated answer. Next you need to continue dividing until you get zero. If there are not enough signs in the dividend for complete division, zeros should be used as them.

Similarly, 2 integers are divided into a column if all the digits of the dividend have been removed and the complete division has not yet been completed. In this case, after removing the last digit of the dividend, a decimal point is placed in the resulting answer, and zeros are used as the removed digits. Those. the dividend here is essentially represented as a decimal fraction with a zero fractional part.

To divide a decimal fraction (or an integer) by a decimal number, you must multiply the dividend and divisor by the number 10 n, in which the number of zeros is equal to the number of digits after the decimal point in the divisor. In this way, you get rid of the decimal point in the fraction you want to divide by. Further, the division process coincides with that described above.
Graphical representation of decimal fractions
Decimal fractions are represented graphically using a coordinate line. To do this, individual segments are further divided into 10 equal parts, just as centimeters and millimeters are marked simultaneously on a ruler. This ensures that decimals are displayed accurately and can be compared objectively.
In order for the divisions on individual segments to be identical, you should carefully consider the length of the single segment itself. It should be such that the convenience of additional division can be ensured.
fractional number.
Decimal notation of a fractional number is a set of two or more digits from $0$ to $9$, between which there is a so-called \textit (decimal point).
Example 1
For example, $35.02$; $100.7$; $123\$456.5; $54.89$.
The leftmost digit in the decimal notation of a number cannot be zero, the only exception being when the decimal point is immediately after the first digit $0$.
Example 2
For example, $0.357$; $0.064$.
Often the decimal point is replaced with a decimal point. For example, $35.02$; $100.7$; $123\456.5$; $54.89$.
Decimal definition
Definition 1
Decimals-- these are fractional numbers that are represented in decimal notation.
For example, $121.05; $67.9$; $345.6700$.
Decimals are used to more compactly write proper fractions, the denominators of which are the numbers $10$, $100$, $1\000$, etc. and mixed numbers, the denominators of the fractional part of which are the numbers $10$, $100$, $1\000$, etc.
For example, the common fraction $\frac(8)(10)$ can be written as a decimal $0.8$, and the mixed number $405\frac(8)(100)$ can be written as a decimal $405.08$.
Reading Decimals
Decimal fractions, which correspond to regular fractions, are read the same as ordinary fractions, only the phrase “zero integers” is added in front. For example, the common fraction $\frac(25)(100)$ (read “twenty-five hundredths”) corresponds to the decimal fraction $0.25$ (read “zero point twenty-five hundredths”).
Decimal fractions that correspond to mixed numbers are read the same as mixed numbers. For example, the mixed number $43\frac(15)(1000)$ corresponds to the decimal fraction $43.015$ (read “forty-three point fifteen thousandths”).
Places in decimals
In writing a decimal fraction, the meaning of each digit depends on its position. Those. in decimal fractions the concept also applies category.
Places in decimal fractions up to the decimal point are called the same as places in natural numbers. The decimal places after the decimal point are listed in the table:
Figure 1.
Example 3
For example, in the decimal fraction $56.328$, the digit $5$ is in the tens place, $6$ is in the units place, $3$ is in the tenths place, $2$ is in the hundredths place, $8$ is in the thousandths place.
Places in decimal fractions are distinguished by precedence. When reading a decimal fraction, move from left to right - from senior rank to younger.
Example 4
For example, in the decimal fraction $56.328$, the most significant (highest) place is the tens place, and the low (lowest) place is the thousandths place.
A decimal fraction can be expanded into digits similar to the digit decomposition of a natural number.
Example 5
For example, let's break down the decimal fraction $37.851$ into digits:
$37,851=30+7+0,8+0,05+0,001$
Ending decimals
Definition 2
Ending decimals are called decimal fractions, the records of which contain a finite number of characters (digits).
For example, $0.138$; $5.34$; $56.123456$; $350,972.54.
Any finite decimal fraction can be converted to a fraction or a mixed number.
Example 6
For example, the final decimal fraction $7.39$ corresponds to the fractional number $7\frac(39)(100)$, and the final decimal fraction $0.5$ corresponds to the proper common fraction $\frac(5)(10)$ (or any fraction which is equal to it, for example, $\frac(1)(2)$ or $\frac(10)(20)$.
Converting a fraction to a decimal
Converting fractions with denominators $10, 100, \dots$ to decimals
Before converting some proper fractions to decimals, they must first be “prepared.” The result of such preparation should be the same number of digits in the numerator and the same number of zeros in the denominator.
The essence of “preliminary preparation” of proper ordinary fractions for conversion to decimal fractions is adding such a number of zeros to the left in the numerator that the total number of digits becomes equal to the number of zeros in the denominator.
Example 7
For example, let's prepare the fraction $\frac(43)(1000)$ for conversion to a decimal and get $\frac(043)(1000)$. And the ordinary fraction $\frac(83)(100)$ does not need any preparation.
Let's formulate rule for converting a proper common fraction with a denominator of $10$, or $100$, or $1\000$, $\dots$ into a decimal fraction:
write $0$;
after it put a decimal point;
write down the number from the numerator (along with added zeros after preparation, if necessary).
Example 8
Convert the proper fraction $\frac(23)(100)$ to a decimal.
Solution.
The denominator contains the number $100$, which contains $2$ and two zeros. The numerator contains the number $23$, which is written with $2$.digits. This means that there is no need to prepare this fraction for conversion to a decimal.
Let's write $0$, put a decimal point and write down the number $23$ from the numerator. We get the decimal fraction $0.23$.
Answer: $0,23$.
Example 9
Write the proper fraction $\frac(351)(100000)$ as a decimal.
Solution.
The numerator of this fraction contains $3$ digits, and the number of zeros in the denominator is $5$, so this ordinary fraction must be prepared for conversion to a decimal. To do this, you need to add $5-3=2$ zeros to the left in the numerator: $\frac(00351)(100000)$.
Now we can form the desired decimal fraction. To do this, write down $0$, then add a comma and write down the number from the numerator. We get the decimal fraction $0.00351$.
Answer: $0,00351$.
Let's formulate rule for converting improper fractions with denominators $10$, $100$, $\dots$ into decimal fractions:
write down the number from the numerator;
Use a decimal point to separate as many digits on the right as there are zeros in the denominator of the original fraction.
Example 10
Convert the improper fraction $\frac(12756)(100)$ to a decimal.
Solution.
Let's write down the number from the numerator $12756$, then separate the digits on the right with a decimal point $2$, because the denominator of the original fraction $2$ is zero. We get the decimal fraction $127.56$.
