Потенциальная энергия взаимодействия точечных зарядов
Пусть два точечных заряда q 1 и q 2 находятся в вакууме на расстоянии r друг от друга. Можно показать, что потенциальная энергия их взаимодействия даётся формулой:
W = kq 1 q 2 /r (3)
Мы принимаем формулу (3) без доказательства. Две особенности данной формулы следует обсудить.
Во-первых, где находится нулевой уровень потенциальной энергии? Ведь потенциальная энергия, как видно из формулы (3), в нуль обратиться не может. Но на самом деле нулевой уровень существует, и находится он на бесконечности. Иными словами, когда заряды расположены бесконечно далеко друг от друга, потенциальная энергия их взаимодействия полагается равной нулю (что логично - в этом случае заряды уже «не взаимодействуют»). Во-вторых, q 1 и q 2 - это снова алгебраические величины зарядов, т.е. заряды с учётом их знака.
Например, потенциальная энергия взаимодействия двух одноимённых зарядов будет положительной. Почему? Если мы отпустим их, они начнут разгоняться и удаляться друг от друга.
Их кинетическая энергия возрастает, стало быть потенциальная энергия - убывает. Но на бесконечности потенциальная энергия обращается в нуль, а раз она убывает к нулю, значит - она является положительной.
А вот потенциальная энергия взаимодействия разноимённых зарядов оказывается отрицательной. Действительно, давайте удалим их на очень большое расстояние друг от друга - так что потенциальная энергия равна нулю - и отпустим. Заряды начнут разгоняться, сближаясь, и потенциальная энергия снова убывает. Но если она была нулём, то куда ей убывать? Только в сторону отрицательных значений.
Формула (3) помогает также вычислить потенциальную энергию системы зарядов, если число зарядов больше двух. Для этого нужно просуммировать энергии каждой пары зарядов. Мы не будем выписывать общую формулу; лучше проиллюстрируем сказанное простым примером, изображённым на рис. 8
Рис. 8. Взаимодействие трёх зарядов
Если заряды q 1 , q 2 , q 3 находятся в вершинах треугольника со сторонами a, b, c, то потенциальная энергия их взаимодействия равна:
W = kq 1 q 2 /a + kq 2 q 3 /b + kq 1 q 3 /c
Потенциал
Из формулы W = - qEx мы видим, что потенциальная энергия заряда q в однородном поле прямо пропорциональна этому заряду. То же самое мы видим из формулы W = kq 1 q 2 /r потенциальная энергия заряда q 1 , находящегося в поле точечного заряда q 2 , прямо пропорциональна величине заряда q 1 . Оказывается, это общий факт: потенциальная энергия W заряда q в любом электростатическом поле прямо пропорциональна величине q:
Величина ц уже не зависит от заряда, является характеристикой поля и называется потенциалом:
Так, потенциал однородного поля E в точке с абсциссой x равен:
Напомним, что ось X совпадает с линией напряжённости поля. Мы видим, что с ростом x потенциал убывает. Иными словами, вектор напряжённости поля указывает направление убывания потенциала. Для потенциала поля точечного заряда q на расстоянии r от него имеем:
Единицей измерения потенциала служит хорошо известный вам вольт. Из формулы (5) мы видим, что В = Дж / Кл.
Итак, теперь у нас есть две характеристики поля: силовая (напряжённость) и энергетическая (потенциал). У каждой из них имеются свои преимущества и недостатки. Какую именно характеристику удобнее использовать - зависит от конкретной задачи.
Если электрическое тело действует на электрически заряженные тела, то оно способно совершить работу по перемещению заряженных тел. Электростатическое поле, создаваемое точечным зарядом, является центральным, то есть сила, действующая на точечный заряд в таком поле, направлена вдоль прямой, соединяющей заряд-источник и пробный заряд. Ранее мы показали, что любая центральная сила является потенциальной, то есть работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела.
Вкратце напомним доказательство этого важнейшего утверждения. Пусть точечный пробный заряд q движется в центральном поле, создаваемом неподвижным зарядом Q (Рис. 174). Сила, действующая на пробный заряд, определяется законом Кулона
Где - вектор, проведенный от заряда источника Q, к точке A, в которой находится пробный заряд. При движении заряда по дугам окружностей с центром на заряде Q (например, по дугам AB, CD) работа электрической силы равна нулю, так векторы силы и перемещения взаимно перпендикулярны. При движении же в радиальном направлении (например, по отрезкам BC, DE) работа зависит только от начального и конечного расстояния до заряда источника. Так работы электростатического поля при перемещении по отрезкам DE и D1E1 , очевидно равны. Самое красивое доказательство этого утверждения связано с симметрией поля – повернем нашу систему вокруг оси проходящей через источник, так, что бы отрезок D1E1 совпал с отрезком DE - распределение поля при этом не изменится, почему должна изменится работа поля?
Так как для напряженности электростатического поля справедлив принцип суперпозиции, то потенциальным является любое электростатическое поле. Действительно, пусть точечный заряд q находится в электрическом поле, создаваемым системой неподвижных точечных зарядов Q1, Q2, … ,QN . При перемещении заряда на малый вектор перемещения, по определению, электрическое поле совершит работу, где
Результирующая сила, действующая на движущийся заряд q, равная сумме сил, действующих со стороны каждого из неподвижных точечных зарядов Qk. Работа этой силы может быть вычислена по формуле
Для того, чтобы вычислить работу по конечному участку траектории, необходимо разбить траекторию на малые участки (Рис. 175), затем с помощью формулы (1) вычислить работу на каждом малом участке, после чего их просуммировать
. (2)Фактически, данная сумма является двойной, так как каждая результирующая сила, является суммой сил, в соответствии с формулой (1). Обратим внимание, что в формуле (2) результирующая сила изменяется, так как вычисляется в разных точках траектории.
Как мы показали ранее, работа электрического поля точечного заряда не зависит от формы траектории, то есть каждое слагаемое из формулы (1) не зависит от формы траектории, следовательно, и вся сумма не зависит от формы траектории. Таким образом, любое электростатическое поле является потенциальным.
Следовательно, для точечного заряда, находящегося в электростатическом поле можно ввести потенциальную энергию взаимодействия U(x,y,z). Эта функция имеет следующий физический смысл: работа электрического поля при перемещения точечного заряда из одной точки с координатами (x1,y1,z1) в другую, с координатами (x2,y2,z2) равна изменению потенциальной энергии, взятому с противоположным знаком:
. (3)Изменение знака в данном определении достаточно логично: если электрическое поле совершило положительную работу (A > 0), то его энергия уменьшается (ΔU < 0). Для вычисления работы силы взаимодействия между двумя точечными заряженными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (Рис. 176). Если построить зависимость силы взаимодействия между зарядами от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (Рис. 177). Зависимость силы электростатического взаимодействия от расстояния аналогична силе гравитационного взаимодействия, с одним существенным отличием: гравитационная сила всегда есть сила притяжения, а электрическая может быть как силой притяжения, так и силой отталкивания. В частности два положительных заряда отталкиваются. Поэтому выражение для работы электрического поля, будет аналогично формуле для работы гравитационной силы, но иметь противоположный знак
Эта работа равна уменьшению потенциальной энергии взаимодействия, то есть Из этого выражения можно определить выражение для потенциальной энергии электростатического взаимодействия двух точечных зарядов . (4) При таком определении потенциальная энергия взаимодействия двух зарядов одного знака положительна и стремится к нулю при бесконечном расстоянии между телами. Сила взаимодействия зарядов противоположных знаков направлена в противоположную сторону, поэтому работа этой силы при увеличении расстояния между зарядами будет отрицательна. Однако нам нет необходимости делать какие-то дополнительные оговорки, так как формула (4) автоматически учитывает знаки зарядов – если заряды противоположны, то их произведение (соответственно и энергия) отрицательны. Знак потенциальной энергии взаимодействия зарядов имеет очень наглядный смысл. Заряды одного знака отталкиваются, поэтому при их «разбегании» на бесконечно большое расстояние, электрическое поле совершит положительную работу – следовательно, изначально система этих зарядов обладает способностью совершить работу, поэтому ее энергия положительна, при удалении зарядов друг от друга их энергия уменьшается до нуля. Заряды противоположных знаков притягиваются, для того чтобы удалить их на бесконечно большое расстояние, внешние силы должны совершать положительную работу. При этом энергия пары зарядов должна возрастать, следовательно, изначально она отрицательна, а при удалении зарядов друг от друга возрастает до нуля. В целом обычная ситуация – притяжению соответствует отрицательная энергия, а отталкиванию - положительная. Отметим только, что такая очевидность справедлива только при выборе нулевого уровня потенциальной энергии на бесконечности. Формула (4) определяет потенциальную энергию взаимодействия двух точечных заряженных тел. Величины зарядов тел Q и q входят, как и следовало ожидать, в эту формулу симметрично. Подразделение зарядов на заряд-источник и пробный заряд является условным, их вполне можно поменять местами. Поэтому данную формулу предпочтительнее записывать в симметричном виде: энергия взаимодействия двух точечных зарядов q1 и q2 равна , (5)и имеет смысл работы, совершаемой полем при увеличении расстояния между зарядами от r до бесконечности, независимо от того, движется ли первый заряд, или второй, или движутся оба заряда, наконец, не зависимо от траекторий движения обоих зарядов. Далее, нельзя сказать какому именно заряду «принадлежит» эта энергия, в дальнейшем мы покажем, что энергия взаимодействия зарядов есть часть энергии самого электростатического поля, то есть она «размазана» по всему пространству, где существует поле, создаваемое этими зарядами. Если система состоит из более чем двух зарядов, то для подсчета энергии взаимодействия этих зарядов необходимо просуммировать энергии взаимодействия всех пар зарядов
здесь Uik - энергия взаимодействия зарядов qi и qk, находящихся на расстоянии rik друг от друга (Рис. 178).
40 Вопрос:
Электростатическое поле - эл. поле неподвижного заряда.
Fэл, действующая на заряд, перемещает его, совершая раборту. В однородном электрическом поле Fэл = qE - постоянная величина
Работа поля (эл. силы) не зависит от формы траектории и на замкнутой траектории = нулю.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Электростатическая энергия - потенциальная энергия системы заряженных тел (т.к. они взаимодействуют и способны совершить работу).
Так как работа поля не зависит от формы траектории, то одновременно
сравнивая формулы работы, получим потенциальную энергию заряда в однородном электростатическом поле
Если поле совершает положительную работу (вдоль силовых линий), то потенциальная энергия
заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия) и наоборот.
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Энергитическая характеристика эл. поля.
Равен отношению потенциальной энергии заряда в поле к этому заряду.
Скалярная величина, определяющая потенциальную энергию заряда в любой точке эл. поля.
Величина потенциала считается относительно выбранного нулевого уровня.
РАЗНОСТЬ ПОТЕНЦИАЛОВ (или иначе НАПРЯЖЕНИЕ)
Это разность потенциалов в начальной и конечной точках траектории заряда.
Напряжение между двумя точками (U) равно разности потенциалов этих точек и равно работе поля по перемещению единичного заряда.
СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ
Работа
сил электрического поля, созданного
зарядом
,
по перемещению заряда из точки 1 в точку 2 равна:
из точки 1 в точку 2 равна:
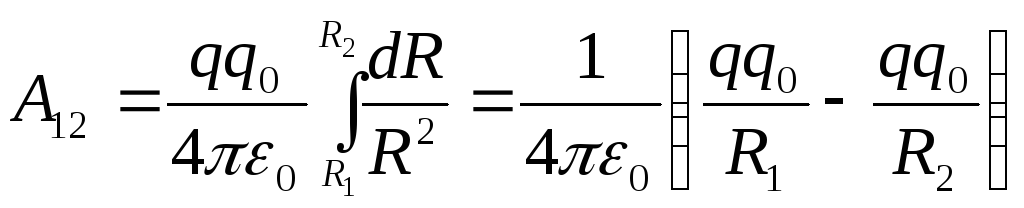 .
.
Работа сил консервативного поля равна убыли потенциальной энергии:
 ,
,
тогда
потенциальная энергия заряда
 в поле заряда
в поле заряда равна:
равна:
 .
.
Значение
константы выбирается таким, чтобы при
удалении заряда на бесконечность (то
есть при
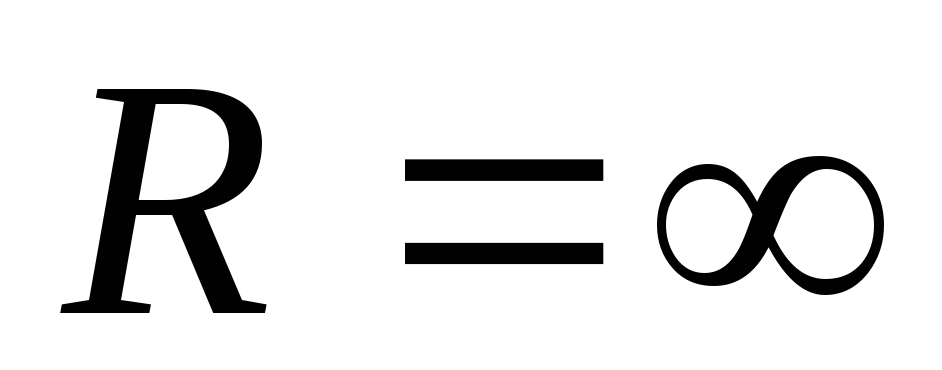 )
потенциальная энергия обратилась бы в
ноль, поэтому
)
потенциальная энергия обратилась бы в
ноль, поэтому
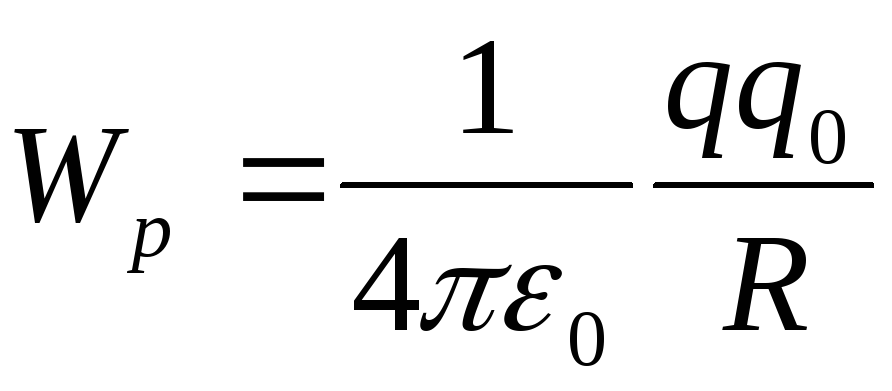 .
.
Ясно,
что разные пробные заряды
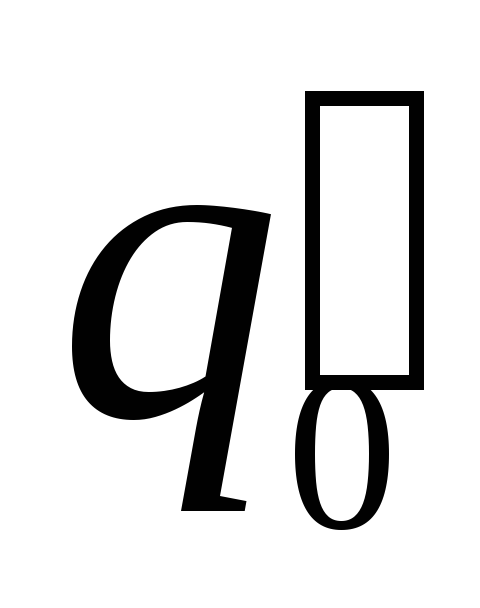 и
и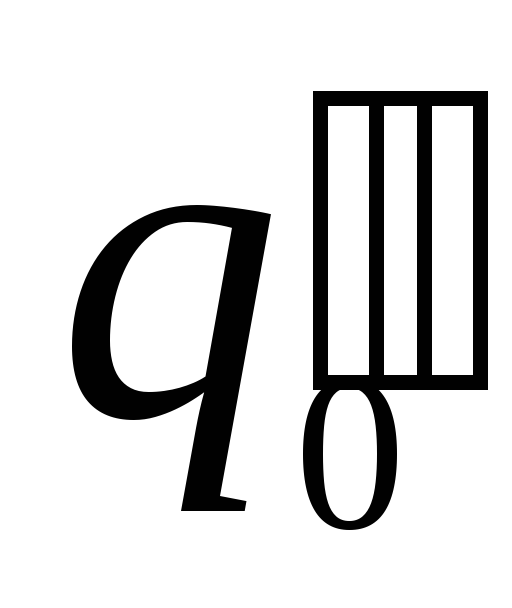 в одной и той же точке поля будут обладать
разной потенциальной энергией
в одной и той же точке поля будут обладать
разной потенциальной энергией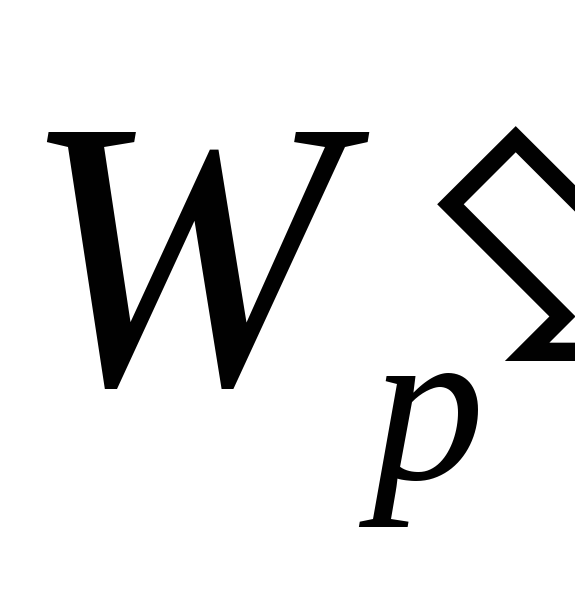 и
и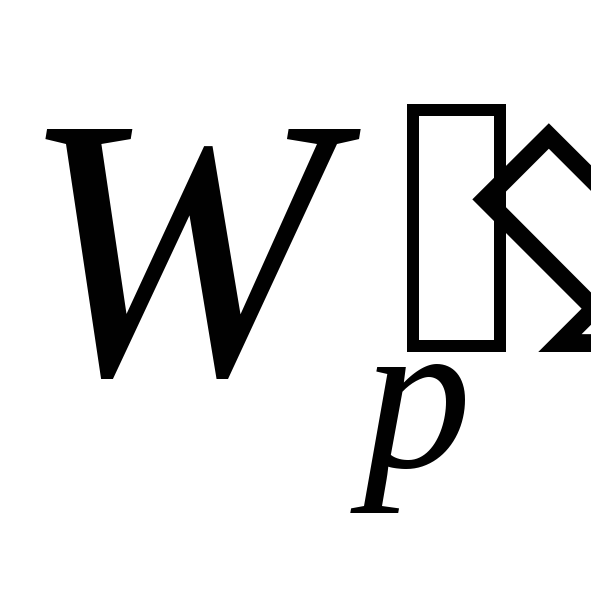 .
Однако отношение
.
Однако отношение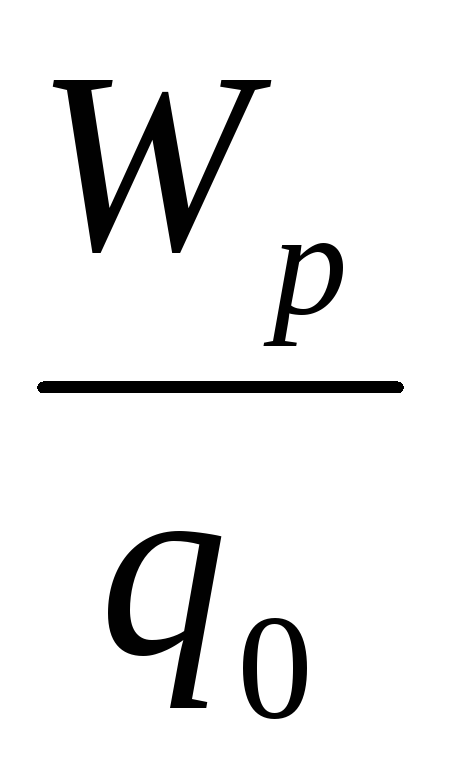 для всех пробных зарядов будет одинаково.
Величина
для всех пробных зарядов будет одинаково.
Величина

называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен
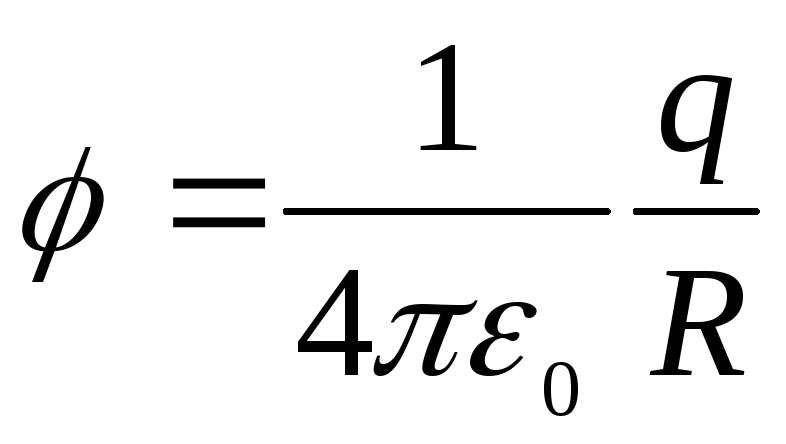 .
.
Если
поле создается системой
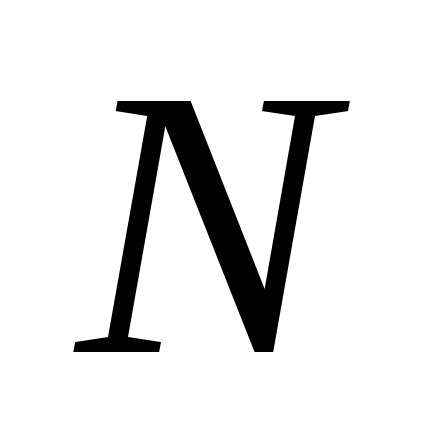 точечных зарядов, то
точечных зарядов, то
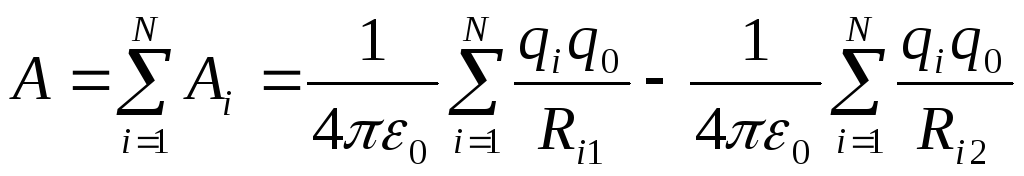 ,
,
где
 - расстояние от заряда
- расстояние от заряда до начального положения заряда
до начального положения заряда ,
, - расстояние от заряда
- расстояние от заряда до конечного положения заряда
до конечного положения заряда (заряд
(заряд перемещается силами поля).
перемещается силами поля).
Тогда
потенциальная энергия заряда в поле системы зарядов:
в поле системы зарядов:
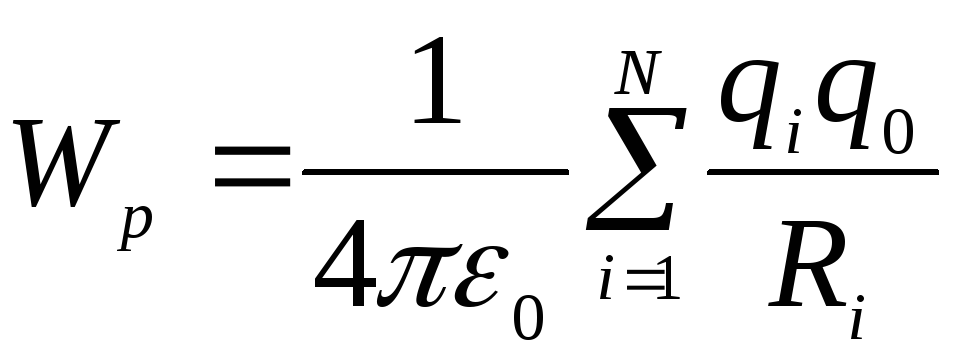 ,
,
а
потенциал
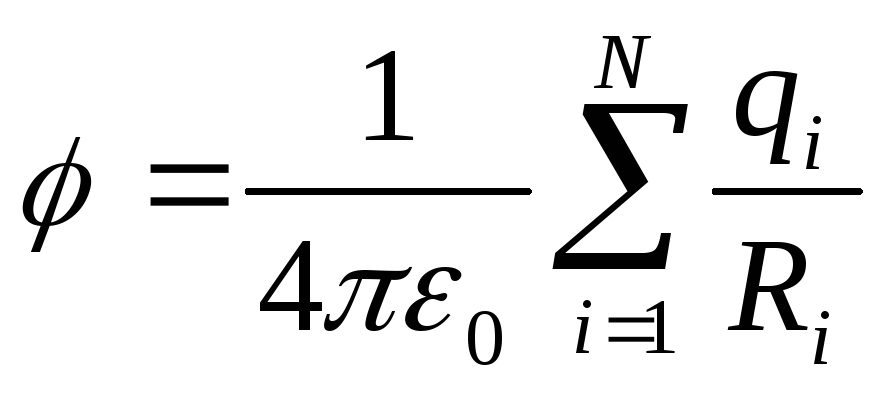
потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Зная
потенциал, можно найти потенциальную
энергию заряда
 в электрическом поле:
в электрическом поле:
 .
.
Работа поля над зарядом:
Работа равна убыли потенциала, умноженной на заряд.
Если заряд удаляется из точки на бесконечность, то работа сил поля равна
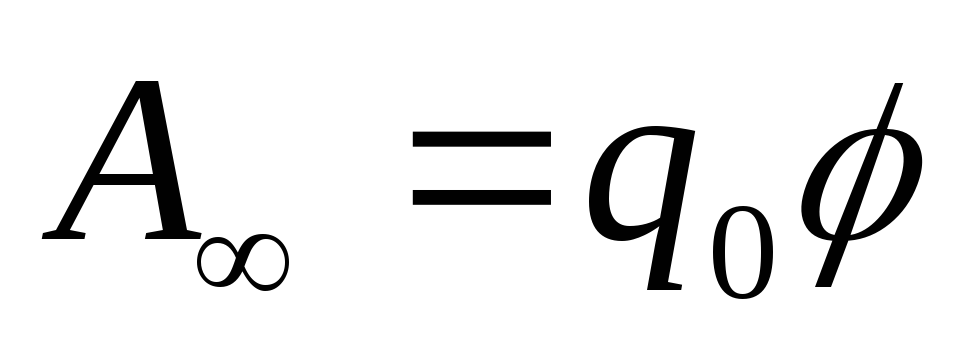
следовательно,
потенциал численно равен отношению
работы, которую совершают силы поля над
положительным зарядом при удалении его
из данной точки на бесконечность, к
величине этого заряда. Потенциал
измеряется в вольтах:
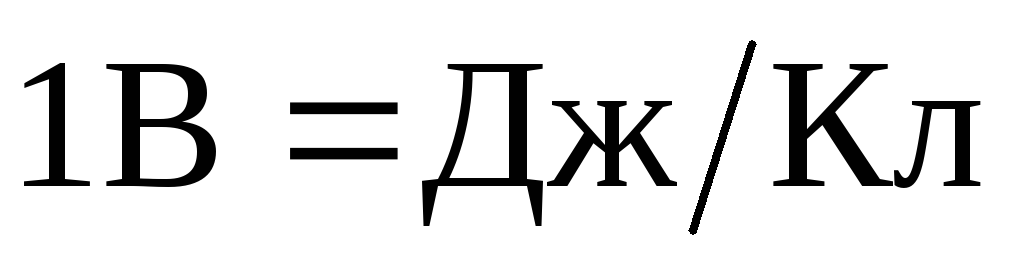 .
.
1.5.Связь между напряженностью и потенциалом
Электрическое
поле можно описывать либо с помощью
векторной величины
 (силовая характеристика), либо с помощью
скаляра
(силовая характеристика), либо с помощью
скаляра (энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
(энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
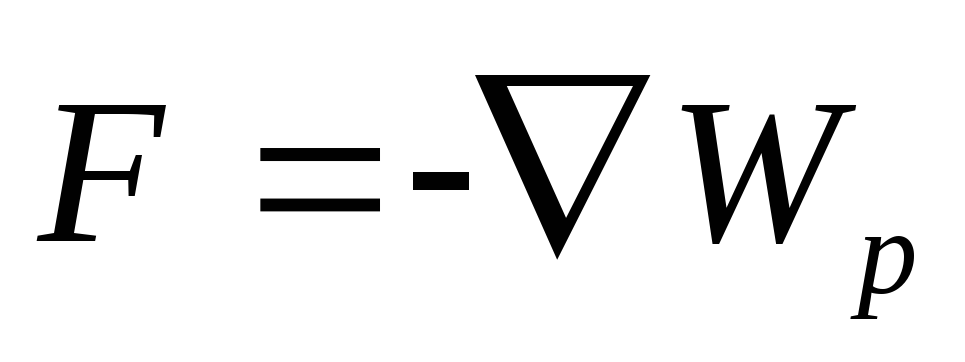 ,
,
где
 - оператор Набла,
- оператор Набла, .
.
Для
заряженной частицы в электрическом
поле:
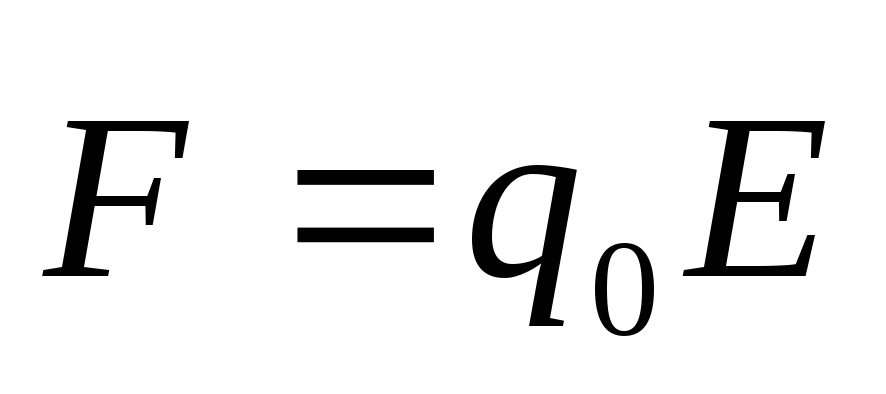 ,
, ,
тогда
,
тогда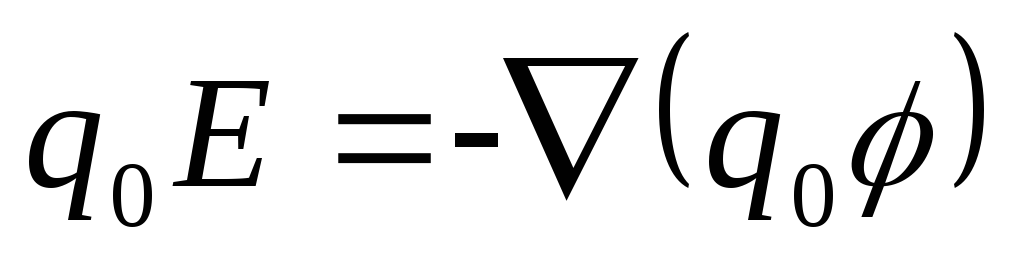 ,
,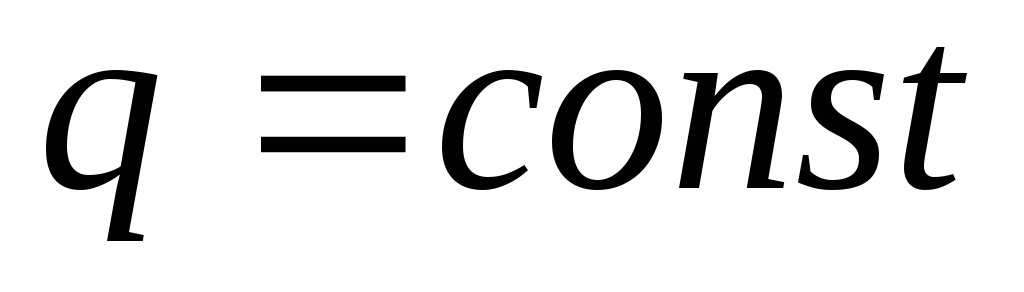 ,
тогда
,
тогда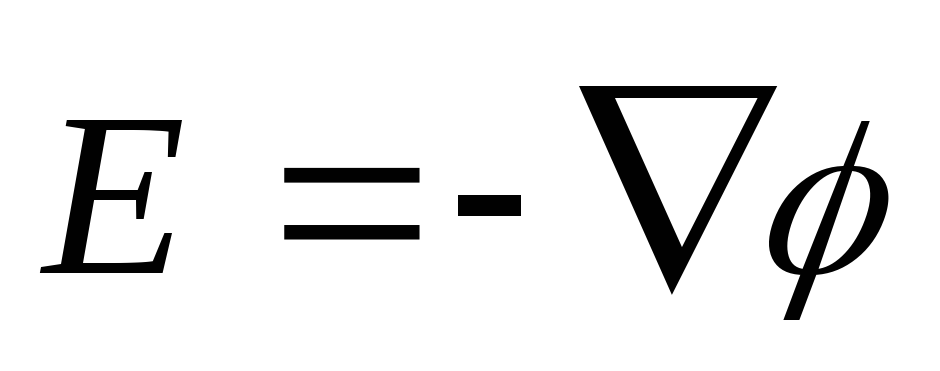 - связь напряженности и потенциала, или
- связь напряженности и потенциала, или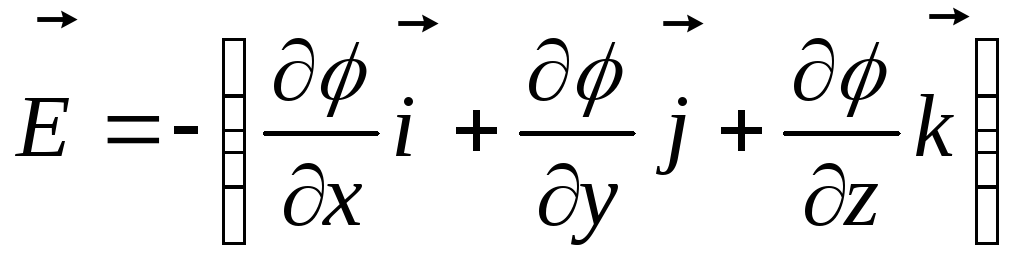 ,
или
,
или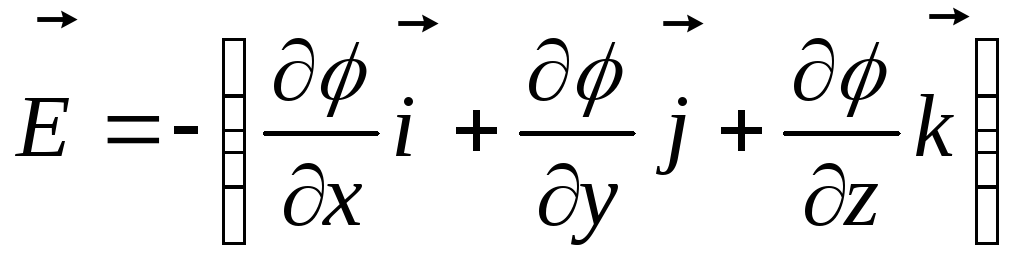 ,
или
,
или -
проекция
вектора
-
проекция
вектора
 на произвольное направление
на произвольное направление равна скорости убывания потенциала
равна скорости убывания потенциала вдоль направления
вдоль направления
 ,
или
,
или
 .
.
Так как градиент потенциала направлен в сторону его возрастания, а численная величина градиента является мерой быстроты этого возрастания, то можно сказать, что напряженность электрического поля есть мера быстроты спадания потенциала, или, просто, что она равна спаду потенциала.
Вернемся к
определению работы поля:
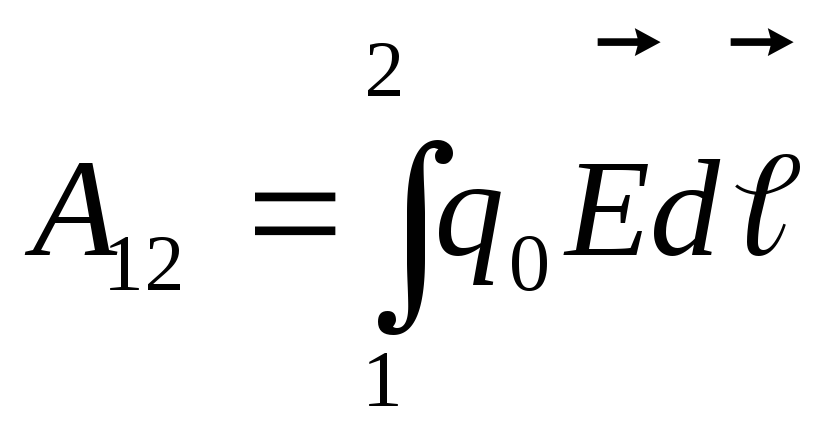 ,
,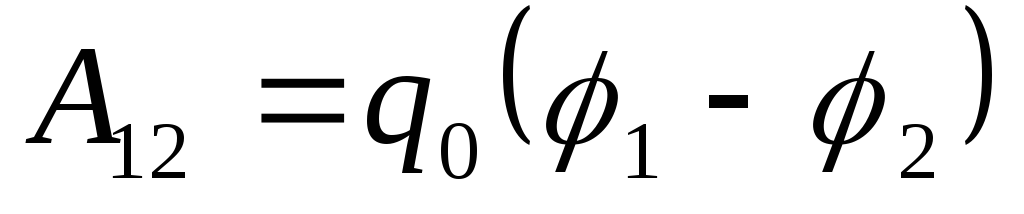 ,
отсюда циркуляция вектора
,
отсюда циркуляция вектора
 на
участке 1=2
равна
на
участке 1=2
равна
 .
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
.
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
Для
обхода по замкнутому контуру:
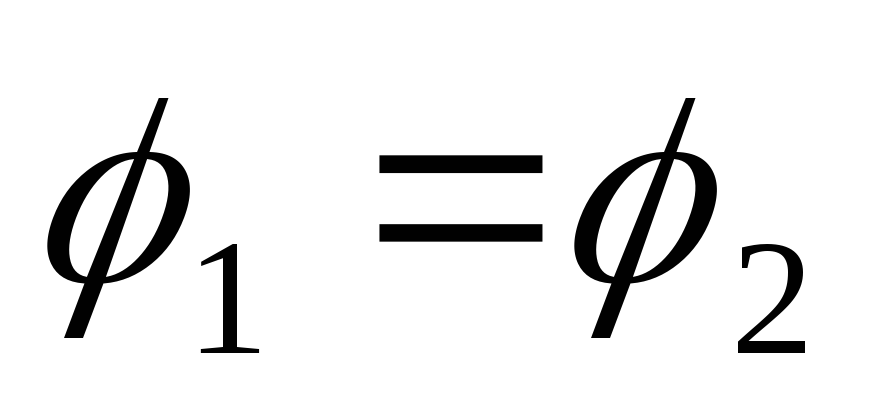 и
и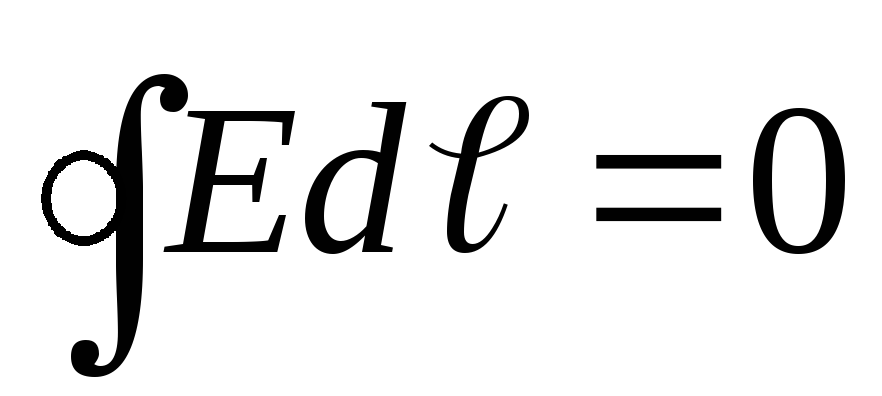 - пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
- пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
1.6. Эквипотенциальные поверхности
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:
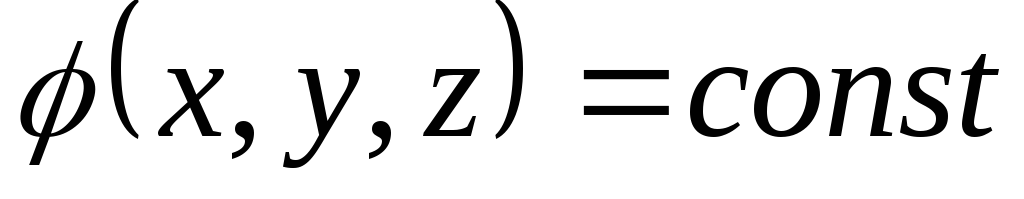
Уравнение эквипотенциальной поверхности.
При
перемещении по эквипотенциальной
поверхности на отрезок
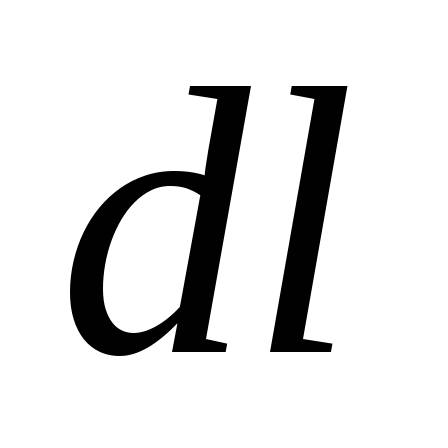 потенциал не изменяется
потенциал не изменяется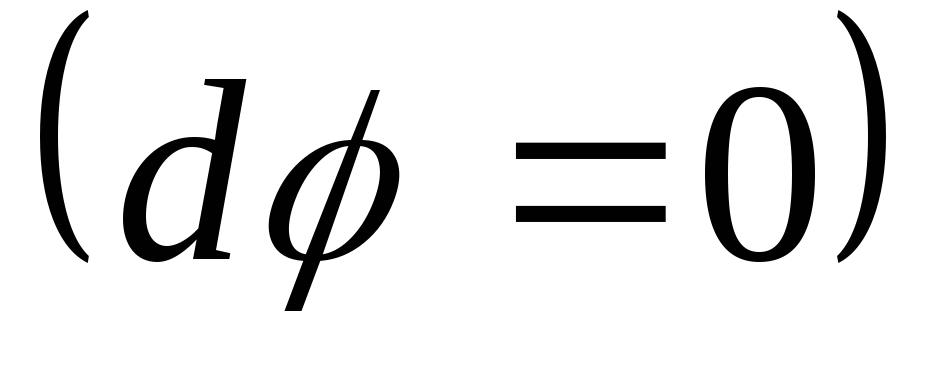 .
Таким образом, касательная к поверхности
составляющая вектора
.
Таким образом, касательная к поверхности
составляющая вектора равна нулю. Тогда вектор
равна нулю. Тогда вектор направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
 Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше
Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше ,
тем больше
,
тем больше .
.
Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.4)
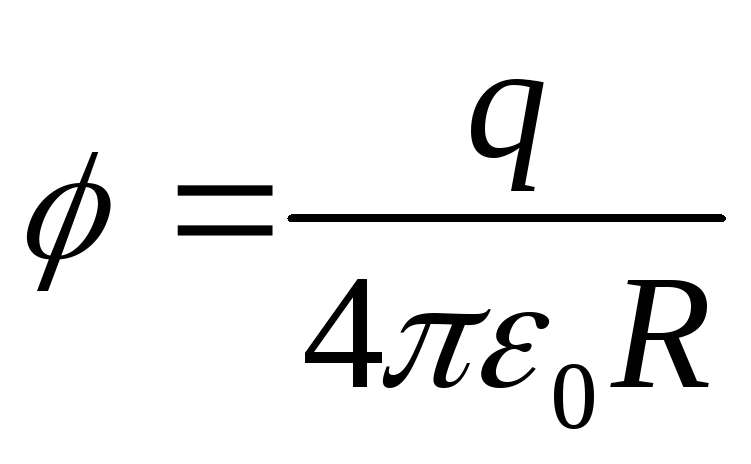 .
.
Таким
образом, эквипотенциальная поверхность
этого заряда будет сферой радиуса
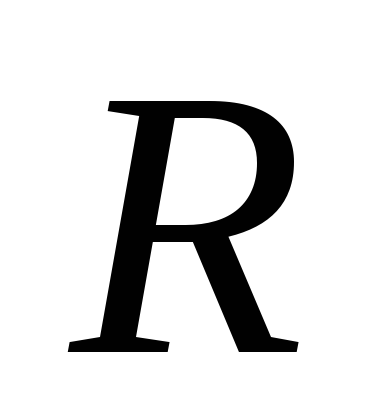 с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
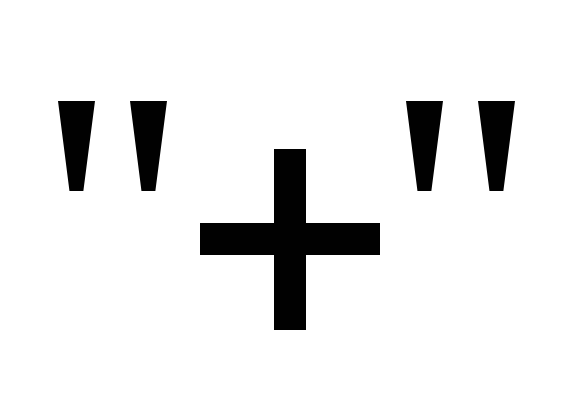 ,
или сходятся к заряду, если он “-”. То
есть вектор
,
или сходятся к заряду, если он “-”. То
есть вектор перпендикулярен эквипотенциальным
поверхностям.
перпендикулярен эквипотенциальным
поверхностям.
Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:
где W п1 и W п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q , изменение потенциальной энергии равно
![]() .
.
При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r 1 и r 2 от заряда Q ,
Если поле создано системой точечных зарядов Q 1 , Q 2 ,¼ , Q n , то изменение потенциальной энергии заряда q в этом поле:
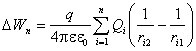 .
.
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q , а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q , находящегося в электрическом поле, созданном другим точечным зарядом Q , получим
![]() ,
,
где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥ ), тогда постоянная C = 0 и предыдущее выражение принимает вид
При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную . В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q :
![]() .
.
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q i (i = 1, 2, ... , n ). Энергия взаимодействия всех n зарядов определится соотношением
![]() ,
,
где r ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля , определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W п / q , откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :
Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q 1, Q 2 ¼ , Q n имеем
![]() ,
,
где r i - расстояние от точки поля, обладающей потенциалом j , до заряда Q i . Если заряд произвольным образом распределен в пространстве, то
![]() ,
,
где r - расстояние от элементарного объема dx , dy , dz до точки (x , y , z ), где определяется потенциал; V - объем пространства, в котором распределен заряд.
Потенциал и работа сил электрического поля.
Основываясь на определении потенциала, можно показать, что работа
сил электрического поля при перемещении точечного заряда q
из одной точки поля в другую равна произведению величины этого заряда
на разность потенциалов в начальной и конечной точках пути, A
=
q
(j
1
-
j
2
)
.
Если по аналогии с потенциальной энергией считать, что в точках,
бесконечно удалённых от электрических зарядов - источников поля, потенциал
равен нулю, то работу сил электрического поля при перемещении заряда q
из точки 1 в бесконечность можно представить как A
¥
=
q
j
1 .
Таким образом, потенциал â данной точке электростатического
поля - это физическая величина, численно равная работе,
совершаемой силами электрического поля при перемещении единичного положительного
точечного заряда из данной точки поля в бесконечно удаленную
: j
= A
¥
/ q
.
В некоторых случаях потенциал электрического поля нагляднее определяется
как физическая величина, численно равная работе
внешних сил против сил электрического поля при перемещении единичного
положительного точечного заряда из бесконечности в данную точку
. Последнее
определение удобно записать следующим образом:
В современной науке и технике, особенно при описании явлений, происходящих в микромире, часто используется единица работы и энергии, называемая электрон-вольтом (эВ). Это работа, совершаемая при перемещении заряда, равного заряду электрона, между двумя точками с разностью потенциалов 1 В: 1 эВ = 1,60× 10 - 1 9 Кл× 1 В = 1,60× 10 - 1 9 Дж.
Вопросы
1) Дайте определение потенциала данной точки поля и разности потенциалов двух точек поля.
2) Приведите графики зависимостей напряженности поля и потенциала от расстояния для равномерно заряженной сферической поверхности. Дайте их объяснение и обоснование.
Энергия системы точечных зарядов как сумма энергия парного взаимодействия зарядов (и принцип суперпозиции)
Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:
где W п1 и W п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q , изменение потенциальной энергии равно
![]() .
.
При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r 1 и r 2 от заряда Q ,
Если поле создано системой точечных зарядов Q 1 , Q 2 ,¼, Q n , то изменение потенциальной энергии заряда q в этом поле:
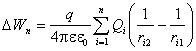 .
.
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q , а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q , находящегося в электрическом поле, созданном другим точечным зарядом Q , получим
![]() ,
,
где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид
При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную . В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q :
![]() .
.
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q i (i = 1, 2, ... ,n ). Энергия взаимодействия всех n зарядов определится соотношением
![]() ,
,
где r ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля , определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W п / q , откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e:
Принцип суперпозиции. Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q 1, Q 2 ¼, Q n имеем
![]() ,
,
где r i - расстояние от точки поля, обладающей потенциалом j, до заряда Q i . Если заряд произвольным образом распределен в пространстве, то
![]() ,
,
где r - расстояние от элементарного объема dx , dy , dz до точки (x , y , z ), где определяется потенциал; V - объем пространства, в котором распределен заряд.
Потенциал и работа сил электрического поля. Основываясь на определении потенциала, можно показать, что работа сил электрического поля при перемещении точечного заряда q из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов в начальной и конечной точках пути, A = q (j 1 - j 2). Если по аналогии с потенциальной энергией считать, что в точках, бесконечно удалённых от электрических зарядов - источников поля, потенциал равен нулю, то работу сил электрического поля при перемещении заряда q из точки 1 в бесконечность можно представить как A ¥ = q j 1 . Таким образом, потенциал â данной точке электростатического поля - этофизическая величина, численно равная работе, совершаемой силами электрического поля при перемещении единичного положительного точечного заряда из данной точки поля в бесконечно удаленную : j = A ¥ / q . В некоторых случаях потенциал электрического поля нагляднее определяется какфизическая величина, численно равная работе внешних сил против сил электрического поля при перемещении единичного положительного точечного заряда из бесконечности в данную точку . Последнее определение удобно записать следующим образом:
В современной науке и технике, особенно при описании явлений, происходящих в микромире, часто используется единица работы и энергии, называемая электрон-вольтом (эВ). Это работа, совершаемая при перемещении заряда, равного заряду электрона, между двумя точками с разностью потенциалов 1 В: 1 эВ = 1,60×10 -19 Кл×1 В = 1,60×10 -19 Дж.
Интегральное представление энергии непрерывного распределения зарядов, c равнение со случаем энергии системы точечных зарядов
Пусть в элементе объема находится заряд. Для определения энергии взаимодействия всех элементовв объеме V можно использовать формулу(12.4). , перейдя в ней от суммы к интегралу:
Где - потенциал, создаваемый всеми зарядами в точке нахождения заряда.
На первый заряд формулы (12.4) и (12.5) кажутся аналогичными, тем более что (12.5) “выведена” из (12.4). Однако между ними существует принципиальное различие. Формула (12.4) учитывает лишь энергию взаимодействия между заряженными шарами, но не учитывает энергию взаимодействия между элементами зарядов, находящихся на каждом шаре. А (12.5) учитывает и первое, и второе.
Учитывая сказанное, энергию взаимодействия зарядов можно записать в виде:
Величина - это энергия заряженных шаров, учитывающая взаимодействие зарядов между собой на каждом шаре. Собственная энергия зависит от законов распределения зарядов шара и значений зарядов. Если имеется уединенный шар, то.
Тогда ![]() (12.7)
(12.7)
Это означает, что собственная энергия точечного заряда равна бесконечности.
Но при . Это приводит к серьезным трудностям при использовании модели точечных зарядов.
Электрическая энергия заряженных уединенного проводника и конденсатора
Если
уединенный проводник имеет заряд q, то
вокруг него существует электрическое
поле, потенциал которого на поверхности
проводника равен ,
а емкость - С. Увеличим заряд на величину
dq. При переносе заряда dq из бесконечности
должна быть совершена работа равная![]() .
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю.
Тогда
.
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю.
Тогда
![]()
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
![]()
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
![]()
Применяя соотношение , можно получить следующие выражения для потенциальной энергии W:
Энергия электростатического поля, выраженная в виде объемного интеграла от векторов напряжённости Е и электрического смещения D .

Выражение силы, действующей на проводник, погруженный в жидкий или газообразный диэлектрик, через объемную плотность энергии электрического поля вблизи проводника.
При наличии среды вычисление сил, действующих на проводники и диэлектрики, усложняется.
Прежде всего выражение для объемной силыстановится несправедливым, даже если под понимать молекулярную плотность заряда. Это связано с тем, чтоесть средняя макроскопическая плотность, которая не учитывает поляризацию отдельных молекул. Между тем в неоднородном электрическом поле на поляризованную молекулу действует сила. Можно было бы попробовать усреднить эту силу по объему, но такая процедура наталкивается на значительные трудности. Воспользуемся энергетическим методом вычисления сил.
Рассмотрим
несколько типичных задач. Найдем силу,
действующую на диэлектрический шар,
помещенный в слабо неоднородное поле.
Последнее условие означает, что поле
должно мало меняться на размере шара.
Тогда дипольный момент шара
будет приблизительно такой же, как и в
однородном поле: где
Е - внешнее поле (в отсутствие шара).
Так как момент шара пропорционален
полю, от он ведет себя как квазиупругий диполь и,
следовательно, его энергия в поле .
Произведем теперь виртуальное перемещение
шара во внешнем неоднородном поле и
запишем баланс энергии:
![]() где -
сила, действующая на шар со стороны
поля:
где -
сила, действующая на шар со стороны
поля:
![]() (19.1)
(19.1)
т. е. диэлектрик втягивается в сильное поле. Если (слабый диэлектрик), то выражение (19.1) справедливо для диэлектрика произвольной формы, так как в этом случае можно пренебречь взаимодействием отдельных участков диэлектрика, которые поляризуются независимо друг друга. Тогда объемная сила, действующая на диэлектрик,
![]() (19.2)
(19.2)
т. е. определяется изменением плотности энергии электрического поля при внесении диэлектрика.
Кроме силы, действующей в неоднородном электрическом поле на диэлектрик как целое, в нем возникают еще и внутренние напряжения, называемые стрикционными силами. Рассмотрим пластину диэлектрика, помещенную в плоский конденсатор (рис. 11.5). Ясно, что под действием стрикционных сил пластина несколько

Рис. 11.5. К расчету стрикционных сил.
растянется
вдоль поля. Попробуем вычислить
стрикционные силы в этом примере.
Воспользуемся энергетическим методом.
При небольшем растяжении пластины
изменение энергии поля складывается
из двух частей. Во-первых, в слое энергия
поля в вакууме заменяется
на энергию поля в среде Здесь поле
в вакуумном зазоре, которое не изменяется
при деформации диэлектрика, поскольку
мы принимаем заряд на конденсаторе
неизменным (см. выше). Во-вторых, необходимо
учесть изменение энергии во всем объеме
вещества из-за изменения его плотности,
от которой
зависит диэлектрическая проницаемость: ![]() где
где ![]() .Частная производная взята
здесь при постоянной температуре, чтобы
исключить зависимость от
температуры. Полный баланс энергии на
единицу площади диэлектрика имеет вид
.Частная производная взята
здесь при постоянной температуре, чтобы
исключить зависимость от
температуры. Полный баланс энергии на
единицу площади диэлектрика имеет вид
Отсюда натяжение, действующее на диэлектрик,
![]() (19.4)
(19.4)
можно
рассматривать как разность натяжений
снаружи и
изнутри ![]() диэлектрика,
где Е -электрическое поле внутри
последнего.
диэлектрика,
где Е -электрическое поле внутри
последнего.
Обычно стрикционным давлением называется величина
![]() (19.5)
(19.5)
Это давление не дает вклада в силу, действующую на диэлектрик как целое, при условии, что он окружен вакуумом.
Рассмотрим, наконец, произвольную систему заряженных тел, погруженных в однородный жидкий диэлектрик. Как мы уже знаем, такая среда ослабляет поле в раз, не изменяя его конфигурации. Отсюда, в частности, следует, что энергия поля также в раз меньше, чем в вакууме. Значит, и работа по перемещению зарядов, и силы между телами тоже уменьшаются в раз. На первый взгляд этот вывод кажется тривиальным: раз поле уменьшается в раз, то во столько же раз должна уменьшиться и сила его воздействия на заряд. Однако под полем в среде понимается среднее поле, тогда как действующее на заряд локальное поле зависит от формы полости, т. е. от формы заряженного тела. Чтобы разобраться, в чем здесь дело, вернемся к предыдущему примеру. Пусть диэлектрик является теперь жидким и заполняет весь конденсатор. Тем не менее мы можем представить себе, что между диэлектриком и пластиной конденсатора существует очень
тонкая щель, в которой поле равно так что все предыдущее рассмотрение остается в силе. В таком случае давление поля непосредственно на пластину равно т. е. такое же, как в вакууме, вместо ожидаемого ослабления в раз. Этот пример подтверждает, что сила, действующая со стороны поля на заряженное тело, действительно зависит от формы тела.
Однако жидкий диэлектрик имеет, как правило, механический контакт с телом и тоже действует на него с некоторой силой, которая в рассматриваемом примере дается выражением (19.4). Наконец, нужно учесть еще дополнительное давление в жидкости, возникающее за счет электрического поля и равное стрикционному давлению (19.5). Таким образом, полное давление на пластину
![]() (19.6)
(19.6)
в соответствии с энергетическими соображениями.
Подчеркнем еще раз, что такой простой результат получается только для жидкого однородного диэлектрика. Механический контакт проводников с твердым диэлектриком является, как правило, неопределенным. Кроме того, внутренние упругие напряжения зависят теперь не от локального стрикционного давления, а от сил, действующих на весь диэлектрик.
