System M. linear equations With n unknown called the type system
where a ij. and b I. (i.=1,…,m.; b.=1,…,n.) - Some famous numbers, and x 1, ..., x n - Unknown. In the designation of coefficients a ij. First index i.denotes the number of the equation, and the second j. - The number of the unknown, at which this coefficient is worth.
The coefficients at unknown will be recorded as a matrix 
who let's call system matrix.
Numbers in the right parts of equations b 1, ..., b m called free members.
Total n. numbers c 1, ..., C N called by decision This system, if each equation of the system appeals to the equality after the substitution of numbers into it c 1, ..., C N Instead of relevant unknowns x 1, ..., x n.
Our task will be to find the solution solutions. Three situations may arise:
The system of linear equations having at least one solution is called joint. Otherwise, i.e. If the system does not have solutions, then it is called non-stop.
Consider how to find solutions of the system.
Matrix method for solving systems of linear equations
The matrices make it possible to briefly record the system of linear equations. Let a system of 3 equations with three unknowns be given:
Consider the matrix of the system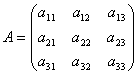 
and matrix columns of unknown and free members 
We find a piece
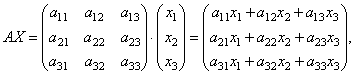
those. As a result of the work, we get left parts of the equations of this system. Then, using the definition of the equality of the matrices, this system can be written as
Or shorter A.∙X \u003d B..
Here the matrix A. and B. Known, and the matrix X. Unknown. It needs to be found, because Its elements are the solution of this system. This equation is called matrix equation.
Let the determinant of the matrix differ from zero | A.| ≠ 0. Then matrix equation Decides as follows. Multiply both parts of the equation on the left side of the matrix A -1., reverse matrix A.:. Insofar as A -1 A \u003d E and E.∙X \u003d X., we obtain the solution of the matrix equation in the form X \u003d a -1 b .
Note that since the reverse matrix can be found only for square matrices, then only those systems in which can be solved by the matrix method. the number of equations coincides with the number of unknown. However, the system matrix record is possible and in the case when the number of equations is not equal to the number of unknown, then the matrix A. will not be square and therefore it is impossible to find a solution to the system in the form of X \u003d a -1 b.
Examples.Solve system equations.
Kramer rule
Consider a system of 3 linear equations with three unknowns:
The determinant of the third order corresponding to the system matrix, i.e. compiled from coefficients at unknown
called determinant system.
We will make three more determinants as follows: Replace in the Determination D sequential 1, 2 and 3 columns by a column of free members
Then you can prove the following result.
Theorem (crawler rule). If the determinant of the system Δ ≠ 0, then the system under consideration has one and only one solution, and
Evidence. So, consider the system of 3 equations with three unknowns. Multiply 1st equation of the system on algebraic supplement A 11. Element a 11., 2nd equation - on A 21. and 3rd - on A 31.:
Match these equations:
Consider each of the brackets and the right side of this equation. By the definition theorem of the determinant for the elements of the 1st column
Similarly, you can show that.
Finally it is easy to notice that 
Thus, we obtain equality :.
Hence, .
Equality and, from where, approval of the theorem are similar.
Thus, we note that if the determinant of the system δ ≠ 0, then the system has a single solution and back. If the system determinant is zero, the system either has an infinite set of solutions or has no solutions, i.e. uncomfortable.
Examples.Solve the system of equations
Gauss method
Previously considered methods can be used when solving only those systems in which the number of equations coincides with the number of unknown, and the system determinant must be different from zero. The Gauss method is more versatile and suitable for systems with any number of equations. It consists in the sequential exclusion of unknowns from the equations of the system.
We will consider the system of three equations with three unknowns:
.
The first equation will be left unchanged, and from the 2nd and 3rd exception terms containing x 1. To do this, the second equation is divided into but 21 and multiply on - but 11, and then put together with the 1st equation. Similarly, the third equation is separated by but 31 and multiply on - but 11, and then put together with the first. As a result, the source system will take the form:
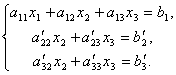
Now from the last equation will exclude the term containing x 2. For this, the third equation is divided into, multiply on and pressing with the second. Then we will have a system of equations:
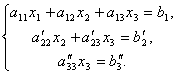
From here from the last equation easy to find x 3.then from the 2nd equation x 2 And finally, from the 1st - x 1.
When using the Gauss method of the equation, if necessary, you can change places.
Often instead of writing new system equations are limited to the fact that the extended system matrix is \u200b\u200bdischarged:
and then lead it to a triangular or diagonal view using elementary transformations.
TO elementary transformations Matrices include the following transformations:
- permutation of rows or columns;
- multiplication of string by a number other than zero;
- adjust to one line Other lines.
Examples: Solve systems of equations by Gauss method.
Thus, the system has infinite set solutions.
Appointment of service. With this online calculator, unknown (x 1, x 2, ..., x n) are calculated in the equation system. The solution is carried out by the method of inverse matrix. Wherein:- the determinant of the matrix A is calculated;
- through algebraic additions is the inverse matrix A -1;
- creating a solution template in Excel;
Instruction. To obtain a solution by the method of inverse matrix, it is necessary to set the dimension of the matrix. Next, in the new dialog box, fill out the matrix A and the vector of the results B.
Recall that by the solution of the system of linear equations, there is any combination of numbers (x 1, x 2, ..., x n), the substitution of which in this system instead of the corresponding unknowns draws each equation of the system into identity.
Linear system algebraic equations Usually recorded as (for 3 variables): see also the solution of matrix equations.
Algorithm Solutions
- The determinant of the matrix A is calculated. If the determinant is zero, the end of the solution. The system has infinite set solutions.
- When the determined is different from zero, the algebraic additions is the reverse matrix A -1.
- The vector of solutions x \u003d (x 1, x 2, ..., x n) is obtained by multiplying the inverse matrix to the result vector b.
Example number 1. Find the solution solving by the matrix method. We write the matrix in the form:
Algebraic additions.
| A 1.1 \u003d (-1) 1 + 1 |
| ∆ 1,1 = (1 (-2)-0 2) = -2 |
| A 1.2 \u003d (-1) 1 + 2 |
| ∆ 1,2 = -(3 (-2)-1 2) = 8 |
| A 1,3 \u003d (-1) 1 + 3 |
| ∆ 1,3 = (3 0-1 1) = -1 |
| A 2.1 \u003d (-1) 2 + 1 |
| ∆ 2,1 = -(-2 (-2)-0 1) = -4 |
| A 2.2 \u003d (-1) 2 + 2 |
| ∆ 2,2 = (2 (-2)-1 1) = -5 |
| A 2.3 \u003d (-1) 2 + 3 |
| ∆ 2,3 = -(2 0-1 (-2)) = -2 |
| A 3.1 \u003d (-1) 3 + 1 |
| ∆ 3,1 = (-2 2-1 1) = -5 |
| A 3.2 \u003d (-1) 3 + 2 |
| ∆ 3,2 = -(2 2-3 1) = -1 |
| 3 |
| -2 |
| -1 |
X t \u003d (1,0,1)
x 1 \u003d -21 / -21 \u003d 1
x 2 \u003d 0 / -21 \u003d 0
x 3 \u003d -21 / -21 \u003d 1
Check:
2 1+3 0+1 1 = 3
-2 1+1 0+0 1 = -2
1 1+2 0+-2 1 = -1
Example number 2. Solve the slam by the method of inverse matrix.
2 x 1 + 3x 2 + 3x 3 + x 4 \u003d 1
3 x 1 + 5x 2 + 3x 3 + 2x 4 \u003d 2
5 x 1 + 7x 2 + 6x 3 + 2x 4 \u003d 3
4 x 1 + 4x 2 + 3x 3 + x 4 \u003d 4
We write the matrix in the form:
Vector B:
B T \u003d (1,2,3,4)
Chief determinant
Minor for (1,1):
= 5 (6 1-3 2)-7 (3 1-3 2)+4 (3 2-6 2) = -3
Minor for (2,1):
= 3 (6 1-3 2)-7 (3 1-3 1)+4 (3 2-6 1) = 0
Minor for (3,1):
= 3 (3 1-3 2)-5 (3 1-3 1)+4 (3 2-3 1) = 3
Minor for (4,1):
= 3 (3 2-6 2)-5 (3 2-6 1)+7 (3 2-3 1) = 3
Determined Minor
∆ = 2 (-3)-3 0+5 3-4 3 = -3
Example number 4. Write a system of equations in matrix form and solve with the help of a reverse matrix.
Solution: XLS.
Example number 5. A system of three linear equations with three unknowns is given. Required: 1) to find its solution using the Cramer formula; 2) Write the system in matrix form and solve it with matrix calculus.
Guidelines. After solving the cramer, find the button "Solution by the method of the return matrix for the source data". You will receive an appropriate solution. Thus, the data is not yet completed.
Decision. Denote by a - matrix of coefficients at unknown; X is an unknown column matrix; B - Matrix-column of free members:
|
B T \u003d (4, -3, -3)
Taking into account these designations, this system of equations takes the following matrix form: A * x \u003d B.
If the matrix A is non-degenerate (its determinant is different from zero, it has a reverse matrix A -1. Multiplying both parts of the equation on A -1, we get: a -1 * a * x \u003d a -1 * b, a -1 * A \u003d E.
This equality is called matrix recording of the solution of the linear equation system. To find a solution of the system of equations, it is necessary to calculate the reverse matrix A -1.
The system will have a solution if the determinant of the matrix A is differ from zero.
We find the main determinant.
∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14
So, the determinant is 14 ≠ 0, so we continue the solution. To do this, we find the return matrix through algebraic additions.
Let them have a nondegenerate matrix A:
| A 1.1 \u003d (- 1) 1 + 1 |
|
| A 1.2 \u003d (- 1) 1 + 2 |
|
| A 1,3 \u003d (- 1) 1 + 3 |
|
| A 2.1 \u003d (- 1) 2 + 1 |
|
| A 2.2 \u003d (- 1) 2 + 2 |
|
| A 2.3 \u003d (- 1) 2 + 3 |
|
| A 3.1 \u003d (- 1) 3 + 1 |
|
| 4 |
| -3 |
| -3 |
| X \u003d 1/14 |
|
∆=4 (0 1-3 (-2))-2 (1 1-3 (-1))+0 (1 (-2)-0 (-1))=16
Transposed matrix
| A 1.2 \u003d (- 1) 1 + 2 |
|
| A 1,3 \u003d (- 1) 1 + 3 |
|
| A 2.1 \u003d (- 1) 2 + 1 |
|
| A 2.2 \u003d (- 1) 2 + 2 |
|
| A 2.3 \u003d (- 1) 2 + 3 |
|
| A 3.1 \u003d (- 1) 3 + 1 |
|
| A 3.2 \u003d (- 1) 3 + 2 |
|
| A 3.3 \u003d (- 1) 3 + 3 | 1/16 |
|
| (4 6)+(1 (-2))+(-1 6) | (4 (-4))+(1 4)+(-1 (-12)) | (4 (-2))+(1 6)+(-1 (-2)) |
| (2 6)+(0 (-2))+(-2 6) | (2 (-4))+(0 4)+(-2 (-12)) | (2 (-2))+(0 6)+(-2 (-2)) |
| (0 6)+(3 (-2))+(1 6) | (0 (-4))+(3 4)+(1 (-12)) | (0 (-2))+(3 6)+(1 (-2)) |
| =1/16 |
|
| A * A -1 \u003d |
|
Example number 7. The solution of matrix equations.
Denote:
| A \u003d. |
|
| A 1.1 \u003d (-1) 1 + 1 |
|
| A 1.2 \u003d (-1) 1 + 2 |
|
| A 1,3 \u003d (-1) 1 + 3 |
|
| A 2.1 \u003d (-1) 2 + 1 |
|
| A 2.2 \u003d (-1) 2 + 2 |
|
| A 2.3 \u003d (-1) 2 + 3 |
|
| A 3.1 \u003d (-1) 3 + 1 |
|
| -12 | 15 | -5 |
| -4 | 5 | -2 |
| 7 | -9 | 3 |
B T \u003d (31,13.10)
X T \u003d (4.05,6.13,7.54)
x 1 \u003d 158/39 \u003d 4.05
x 2 \u003d 239/39 \u003d 6.13
x 3 \u003d 294/39 \u003d 7.54
Check.
-2 4.05+-1 6.13+6 7.54=31
1 4.05+-1 6.13+2 7.54=13
2 4.05+4 6.13+-3 7.54=10
Example number 9. Denote by a - matrix of coefficients at unknown; X is an unknown column matrix; B - Matrix-column of free members:
|
B T \u003d (31,13.10)
X T \u003d (5.21,4.51,6.15)
x 1 \u003d 276/53 \u003d 5.21
x 2 \u003d 239/53 \u003d 4.51
x 3 \u003d 326/53 \u003d 6.15
Check.
-2 5.21+1 4.51+6 6.15=31
1 5.21+-1 4.51+2 6.15=13
2 5.21+4 4.51+-3 6.15=10
Example number 10. The solution of matrix equations.
Denote:
A 11 \u003d (-1) 1 + 1 · -3 \u003d -3; A 12 \u003d (-1) 1 + 2 · 3 \u003d -3; A 21 \u003d (-1) 2 + 1 · 1 \u003d -1; A 22 \u003d (-1) 2 + 2 · 2 \u003d 2;
Reverse matrix A -1.
| -3 | -3 |
| -1 | 2 |
| 1 | -2 |
| 1 | 1 |
| X \u003d. |
|
Matrix method of solving systems of linear equations
Consider the system of linear equations of the following form:
$ \\ left \\ (\\ begin (array) (C) (A_ (11) x_ (1) + a_ (12) x_ (2) + ... + a_ (1n) x_ (n) \u003d b_ (1)) \\\\ (a_ (21) x_ (1) + a_ (22) x_ (2) + ... + a_ (2n) x_ (n) \u003d b_ (2)) \\\\ (...) \\\\ (A_ (N1) x_ (1) + a_ (n2) x_ (2) + ... + a_ (nn) x_ (n) \u003d b_ (n)) \\ End (Array) \\ Right.. $
Numbers $ a_ (ij) (i \u003d 1..n, j \u003d 1..n) $ - system coefficients, numbers $ b_ (i) (i \u003d 1..n) $ - free members.
Definition 1.
In the case when all free members are zero, the system is called homogeneous, otherwise - inhomogeneous.
Each slope can be put into line with several matrices and write the system in the so-called matrix form.
Definition 2.
The system coefficients matrix is \u200b\u200bcalled the system matrix and is indicated, as a rule, the letter $ a $.
A column of free members forms a vector-column, which, as a rule, is denoted by the letter $ b $ and is called the matrix of free members.
Unknown variables form a vector-column, which, as a rule, is indicated by the letter $ x $ and is called an unknown matrix.
The matrix described above have the form:
$ A \u003d \\ left (\\ begin (array) (CCCC) (A_ (11)) & (A_ (12)) & (...) & (A_ (1N)) \\\\ (A_ (21)) & ( A_ (22)) & (...) & (A_ (2N)) \\\\ (...) & (...) & (...) & (...) \\\\ (A_ (N1) ) & (A_ (N2)) & (...) & (A_ (NN)) \\ END (Array) \\ Right), B \u003d \\ Left (\\ Begin (Array) (C) (B_ (1)) \\ \\\\ (x_ (2)) \\\\ (...) \\\\ (x_ (n)) \\ END (Array) \\ Right). $
Using matrices, the slope can be rewritten in the form $ a \\ cdot x \u003d b $. This entry is often called the matrix equation.
Generally speaking, in the matrix form you can record any slope.
Examples of system solutions using reverse matrix
Example 1.
Dana Slaya: $ \\ left \\ (\\ begin (array) (C) (3x_ (1) -2x_ (2) + x_ (3) -x_ (4) \u003d 3) \\\\ (x_ (1) -12x_ (2 ) -X_ (3) -X_ (4) \u003d 7) \\\\ (2x_ (1) -3x_ (2) + x_ (3) -3x_ (4) \u003d 5) \\ END (Array) \\ Right. $. Record The system in matrix form.
Decision:
$ A \u003d \\ left (\\ begin (array) (CCCC) (3) & (-2) & (1) & (-1) \\ (1) & (-12) & (-1) & (-1 -1 ) \\\\ (2) & (-3) & (1) & (-3) \\ END (Array) \\ Right), B \u003d \\ Left (\\ Begin (Array) (C) (3) \\\\ (7) \\\\ (5) \\ END (Array) \\ Right), x \u003d \\ left (\\ begin (array) (c) (x_ (1)) \\\\ (x_ (2)) \\\\ (x_ (3)) \\ $ \\ left (\\ begin (array) (CCCC) (3) & (-2) & (1) & (-1) \\ (1) & (-12) & (-1) & (-1) \\ 2)) \\\\ (x_ (3)) \\ END (Array) \\ Right) \u003d \\ left (\\ begin (array) (C) (3) \\\\ (7) \\\\ (5) \\ END (Array) \\ In the case when the matrix of the system is a square, the slope can be solved by the equation to the matrix method.
Having a matrix equation $ a \\ cdot x \u003d b $ can be expressed from it $ X $ in the following way:
$ A ^ (- 1) \\ cdot a \\ cdot x \u003d a ^ (- 1) \\ Cdot b $
$ A ^ (- 1) \\ Cdot A \u003d E $ (the property of the work of matrices)
$ E \\ Cdot X \u003d A ^ (- 1) \\ Cdot B $
$ E \\ Cdot X \u003d X $ (Property of the Matrix Production)
$ X \u003d a ^ (- 1) \\ Cdot b $
The algorithm for solving the system of algebraic equations using a reverse matrix:
- record the system in matrix;
- calculate the determinant of the system matrix;
- if the determinant of the system matrix is \u200b\u200bdifferent from zero, then we find a reverse matrix;
- solution Solution Calculate according to the formula $ x \u003d a ^ (- 1) \\ Cdot b $.
If the system matrix has a determinant, not equal zeroThis system has a single solution that can be found in a matrix way.
If the system matrix has a determinant equal to zero, then this system cannot be solved by a matrix method.
Example 2.
Dana Slaya: $ \\ left \\ (\\ begin (array) (C) (x_ (1) + 3x_ (3) \u003d 26) \\\\ (-x_ (1) + 2x_ (2) + x_ (3) \u003d 52) \\\\ (3x_ (1) + 2x_ (2) \u003d 52) \\ END (Array) \\ Right. $. Solve the slam by the method of the return matrix, if possible.
Decision:
$ A \u003d \\ left (\\ begin (array) (CCC) (1) & (0) & (3) \\\\ (-1) & (2) & (1) \\\\ (3) & (2) & ( 0) \\ END (Array) \\ Right), B \u003d \\ Left (\\ Begin (Array) (C) (26) \\\\ (52) \\\\ (52) \\ END (Array) \\ Right), x \u003d \\ left (\\ begin (array) (c) (x_ (1)) \\\\ (x_ (2)) \\\\ (x_ (3)) \\ END (Array) \\ RIGHT). $
Finding the determinant of the system matrix:
$ \\ begin (array) (L) (\\ Det a \u003d \\ left | \\ begin (array) (CCC) (1) & (0) & (3) \\\\ (-1) & (2) & (1) \\\\ (3) & (2) & (0) \\ END (Array) \\ Right | \u003d 1 \\ CDOT 2 \\ CDOT 0 + 0 \\ CDOT 1 \\ CDOT 3 + 2 \\ CDOT (-1) \\ CDOT 3-3 \\ CDOT 2 \\ CDOT 3-2 \\ CDOT 1 \\ CDOT 1-0 \\ CDOT (-1) \\ CDot 0 \u003d 0 + 0-6-18-2-0 \u003d -26 \\ Ne 0) \\ End (Array) $ Since the determinant is not equal to zero, then the matrix of the system has a reverse matrix and, therefore, the system of equations can be solved by the inverse matrix method. The solution obtained will be the only one.
Let the system of equations using the reverse matrix:
$ A_ (11) \u003d (- 1) ^ (1 + 1) \\ Cdot \\ Left | \\ Begin (Array) (CC) (2) & (1) \\\\ (2) & (0) \\ END (Array) \\ Right | \u003d 0-2 \u003d -2; A_ (12) \u003d (- 1) ^ (1 + 2) \\ Cdot \\ Left | \\ Begin (Array) (CC) (-1) & (1) \\\\ (3) & (0) \\ END (Array) \\ Right | \u003d - (0-3) \u003d 3; $
$ A_ (13) \u003d (- 1) ^ (1 + 3) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) (-1) & (2) \\\\ (3) & (2) \\ END (Array ) \\ RIGHT | \u003d -2-6 \u003d -8; A_ (21) \u003d (- 1) ^ (2 + 1) \\ cdot \\ left | \\ begin (array) (CC) (0) & (3) \\\\ (2) & (0) \\ END (Array) \\ $
$ A_ (22) \u003d (- 1) ^ (2 + 2) \\ Cdot \\ Left | \\ Begin (Array) (CC) (1) & (3) \\\\ (3) & (0) \\ END (Array) \\ Right | \u003d 0-9 \u003d -9; A_ (23) \u003d (- 1) ^ (2 + 3) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) (1) & (0) \\\\ (3) & (2) \\ End (Array) \\
$ A_ (31) \u003d (- 1) ^ (3 + 1) \\ CDOT \\ LEFT | \\ Begin (Array) (CC) (0) & (3) \\\\ (2) & (1) \\ END (Array) \\ RIGHT | \u003d 0-6 \u003d -6; A_ (32) \u003d (- 1) ^ (3 + 2) \\ Cdot \\ Left | \\ Begin (Array) (CC) (1) & (3) \\\\ (-1) & (1) \\ END (Array) \\ Right | \u003d - (1 + 3) \u003d - 4; $
$ A_ (33) \u003d (- 1) ^ (3 + 3) \\ Cdot \\ Left | \\ Begin (Array) (CC) (1) & (0) \\\\ (-1) & (2) \\ END (Array ) \\ Right | \u003d 2-0 \u003d $ 2
The desired reverse matrix:
$ A ^ (- 1) \u003d \\ FRAC (1) (- 26) \\ CDOT \\ LEFT (\\ Begin (Array) (CCC) (-2) & (6) & (-6) \\\\ (3) & ( -9) & (-4) \\\\ (-8) & (-2) & (2) \\ END (Array) \\ Right) \u003d \\ FRAC (1) (26) \\ CDOT \\ LEFT (\\ Begin (Array) (CCC) (2) & (-6) & (6) \\\\ (-3) & (9) & (4) \\\\ (8) & (2) & (-2) \\ END (Array) \\ Right ) \u003d \\ left (\\ begin (array) (CCC) (\\ FRAC (2) (26)) & (\\ FRAC (-6) (26)) & (\\ FRAC (6) (26)) \\\\ (\\ (26)) & (\\ FRAC (-2) (26)) \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (CCC) (\\ FRAC (1) (13)) & (- \\ (13)) \\\\ (\\ FRAC (4) (13)) & (\\ FRAC (1) (13)) & (- \\ FRAC (1) (13)) \\ END (Array) \\ Right). $
We find the solution of the system:
$ X \u003d \\ left (\\ begin (array) (CCC) (\\ FRAC (1) (13)) & (- \\ FRAC (3) (13)) & (\\ FRAC (3) (13)) \\\\ ( - \\ FRAC (3) (26)) & (\\ FRAC (9) (26)) & (\\ FRAC (2) (13)) \\\\ (\\ FRAC (4) (13)) & (\\ FRAC (1 ) (13)) & (- \\ FRAC (1) (13)) \\ END (Array) \\ Right) \\ Cdot \\ Left (\\ Begin (Array) (C) (26) \\\\ (52) \\\\ (52 ) \\ END (Array) \\ Right) \u003d \\ left (\\ begin (array) (C) (\\ FRAC (1) (13) \\ CDOT 26- \\ FRAC (3) (13) \\ CDOT 52+ \\ FRAC (3 ) (13) \\ CDOT 52) \\\\ (- \\ FRAC (3) (26) \\ CDOT 26+ \\ FRAC (9) (26) \\ CDOT 52+ \\ FRAC (2) (13) \\ CDOT 52) \\\\ Begin (Array) (C) (2-12 + 12) \\\\ (-3 + 18 + 8) \\\\ (8 + 4-4) \\ END (Array) \\ Right) \u003d \\ Left (\\ Begin (Array) (c) (2) \\\\ (23) \\\\ (8) \\ END (Array) \\ Right) $
$ X \u003d \\ left (\\ begin (array) (c) (2) \\\\ (23) \\\\ (8) \\ END (Array) \\ Right) $ is the desired solution of the equation system.
Let there be a square matrix of n-order
Matrix A -1 called inverse matrix In relation to the matrix A, if a * a -1 \u003d e, where e is a single matrix of the N-th order.
Single matrix - Such a square matrix, in which all elements on the main diagonal passing from the upper left corner to the right lower corner are units, and the rest are zeros, for example:
inverse matrix may exist Square matrices only those. For those matrices that the number of rows and columns coincide.
Theorem The conditions of the existence of a return matrix
In order for the matrix to have a reverse matrix, it is necessary and enough to be nondegenerate.
Matrix a \u003d (a1, a2, ... and n) called non-degenerateIf the columns vectors are linearly independent. The number of linearly independent column-column matrix is \u200b\u200bcalled the rag of the matrix. Therefore, we can say that in order to exist inverse matrix, it is necessary and enough so that the ring of the matrix is \u200b\u200bequal to its dimension, i.e. R \u003d n.
Algorithm for the return matrix
- Record into a table to solve systems of equations by the Gauss matrix A and on the right (to the place of the right parts of the equations) attribute to it E. matrix
- Using the transformations of Jordan, lead the matrix A to the matrix consisting of single columns; At the same time, it is necessary to simultaneously convert by the E. matrix
- If necessary, then rearrange the strings (equation) of the last table so that a single matrix E is obtained under the matrix a and the source table.
- Write a reverse matrix A -1, which is located in the last table under the matrix E of the source table.
For the matrix and find a reverse matrix a -1
Solution: Record the matrix A and on the right ascribe a single matrix E. Using the conversion of Jordan, lead the matrix A to the unit matrix E. The calculations are shown in Table 31.1.
We will verify the correctness of the calculations by multiplying the initial matrix A and the return matrix A -1.
As a result of multiplication of matrices, a single matrix was obtained. Consequently, the calculations are made correctly.
Answer: 
The solution of matrix equations
Matrix equations may look:
Ah \u003d in, ha \u003d in, agv \u003d s,
where A, B, C is the specified matrices, which is the desired matrix.
Matrix equations are solved by multiplying the equation for inverse matrices.
For example, to find a matrix from the equation, you must multiply this equation to the left.
Consequently, to find the solution of the equation, you need to find a reverse matrix and multiply it to the matrix, standing in the right part of the equation.
Similarly, other equations are solved.
Solve the equation ah \u003d in if 
Decision: Since the reverse matrix is \u200b\u200bequal (see Example 1)
Matrix method in economic analysis
Along with others, they also use matrix methods. These methods are based on a linear and vector-matrix algebra. Such methods are used for the purpose of analyzing complex and multidimensional economic phenomena. Most often, these methods are used if necessary, comparative assessment of the functioning of organizations and their structural divisions.
In the process of applying matrix analysis methods, several steps can be distinguished.
At the first stage The system of economic indicators is being generated and the initial data matrix is \u200b\u200bbased on it, which is a table in which the system numbers are shown in its separate lines. (i \u003d 1,2, ...., N), and vertical graphs - numbers of indicators (j \u003d 1,2, ...., m).
In the second stage For each vertical column, the largest of the existing values \u200b\u200bof the indicators are detected, which is taken per unit.
After that, all amounts reflected in this graph are divided into the greatest value And the matrix of standardized coefficients is formed.
In the third stage All components of the matrix are elevated in a square. If they have different significance, each matrix indicator is assigned a certain weight coefficient k.. The magnitude of the latter is determined by the expert.
On the latter fourth stage Found values \u200b\u200bof rating ratings R J. Grind them in order to increase or decrease them.
The outlined matrix methods should be used, for example, with a comparative analysis of various investment projects, as well as in assessing other economic indicators of organizations.
The online calculator solves the system of linear equations by the matrix method. A very detailed decision is given. To solve the linear equation system, select the number of variables. Select the method for calculating the return matrix. Then enter the data into the cells and click on the "Calculate" button.
×
A warning
Clear all cells?
Close Clear
Instructions for data entry. The numbers are introduced as integers (examples: 487, 5, -7623, etc.), decimal numbers (eg 67., 102.54, etc.) or fractions. The fraction must be scored in the form A / B, where a and b are whole or decimal numbers. Examples 45/5, 6.6 / 76.4, -7 / 6.7, etc.
Matrix method for solving systems of linear equations
Consider the following system of linear equations:
Considering the definition of the return matrix, we have A. −1 A.=E.where E.- single matrix. Consequently (4) you can record like this:
Thus, to solve the system of linear equations (1) (or (2)), it is sufficient to multiply the inverse A. Matrix on the vector of restrictions b..
Examples of solving a system of linear equations by the matrix method
Example 1. Solve the following system of linear equations by the matrix method:
We will find the reverse matrix A by the method of Jordan-Gauss. On the right side of the matrix A. We write a single matrix:
Let us exclude the elements of the 1st column of the matrix below the main diagonal. To do this, lay a row 2.3 with a string 1 multiplied by -1 / 3, -1 / 3, respectively:
Let us eliminate the elements of the 2nd column of the matrix below the main diagonal. To do this, lay a string 3 with a string 2 multiplied by -24/51:
Let us eliminate the elements of the 2nd column of the matrix above the main diagonal. To do this, lay a string 1 with a string 2 multiplied by -3/17:
Separate the right side of the matrix. The resulting matrix is \u200b\u200ba reverse matrix to A. :
Matrix type of record of the system of linear equations: AX \u003d B.where
We calculate all the algebraic supplements of the matrix A.:
 ,
|
 ,
|
 ,
|
 ,
|
 ,
|
where A. IJ - Algebraic Supplement of the Matrix Element A.intersection i.Line I. j.Both column, and δ - the determinant of the matrix A..
Using the reverse matrix formula, we get: