15. Examples of problem solving

1. Calculate the mass of the isotope nucleus.

Solution. Let's use the formula

.

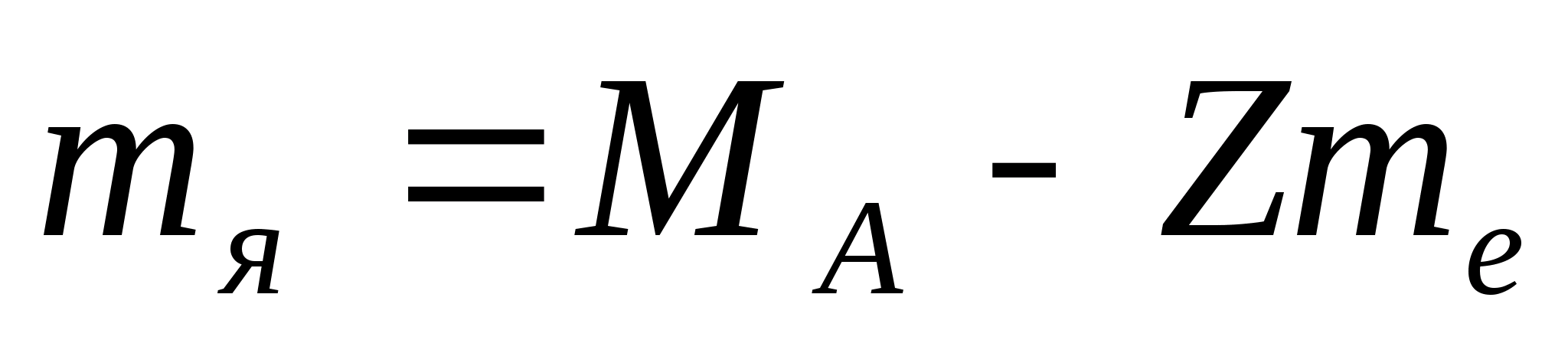Atomic mass of oxygen

=15.9949 amu;

those. Almost all the weight of an atom is concentrated in the nucleus.

2. Calculate the mass defect and nuclear binding energy 3 Li 7 .

Solution. The mass of the nucleus is always less than the sum of the masses of free (located outside the nucleus) protons and neutrons from which the nucleus was formed. Core mass defect ( 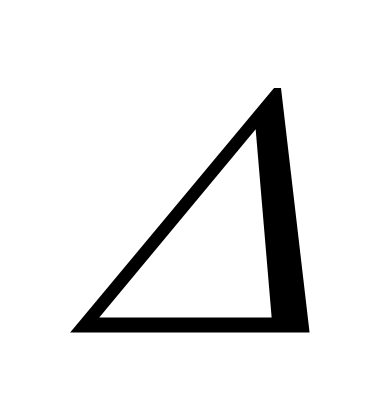m) and is the difference between the sum of the masses of free nucleons (protons and neutrons) and the mass of the nucleus, i.e.

Where Z– atomic number (number of protons in the nucleus); A– mass number (number of nucleons making up the nucleus); m p , m n , m– respectively, the masses of the proton, neutron and nucleus.

Reference tables always give the masses of neutral atoms, but not nuclei, so it is advisable to transform formula (1) so that it includes the mass M neutral atom.

,

.

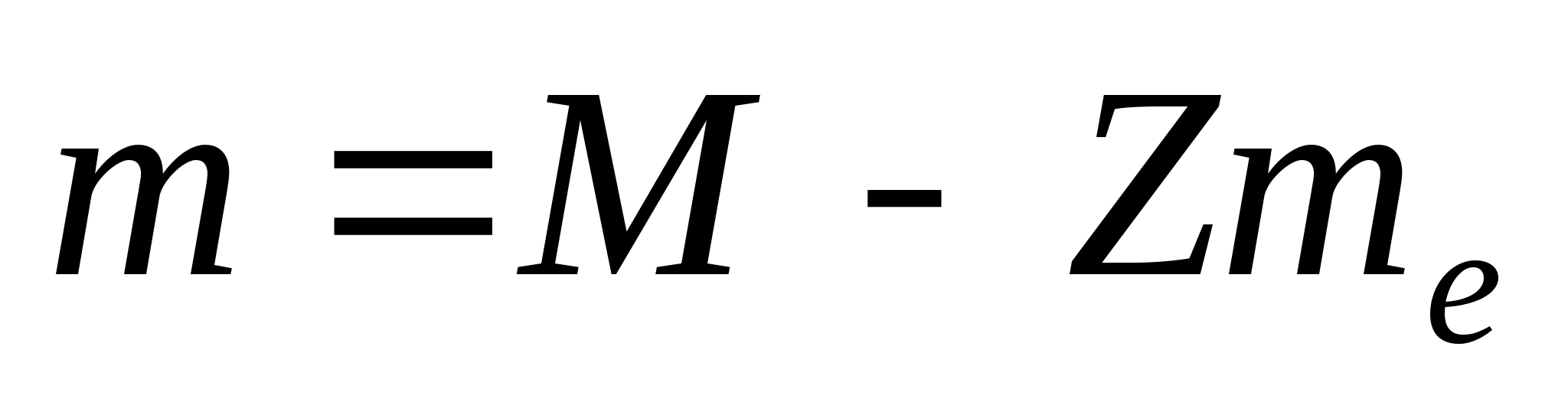Expressing the mass of the nucleus in equality (1) according to the last formula, we obtain

,

Noticing that m p +m e =M H, Where M H– mass of the hydrogen atom, we will finally find

Substituting the numerical values ​​of the masses into expression (2) (according to the data in the reference tables), we obtain

Energy of communication

nucleus is the energy that is released in one form or another during the formation of a nucleus from free nucleons.

In accordance with the law of proportionality of mass and energy

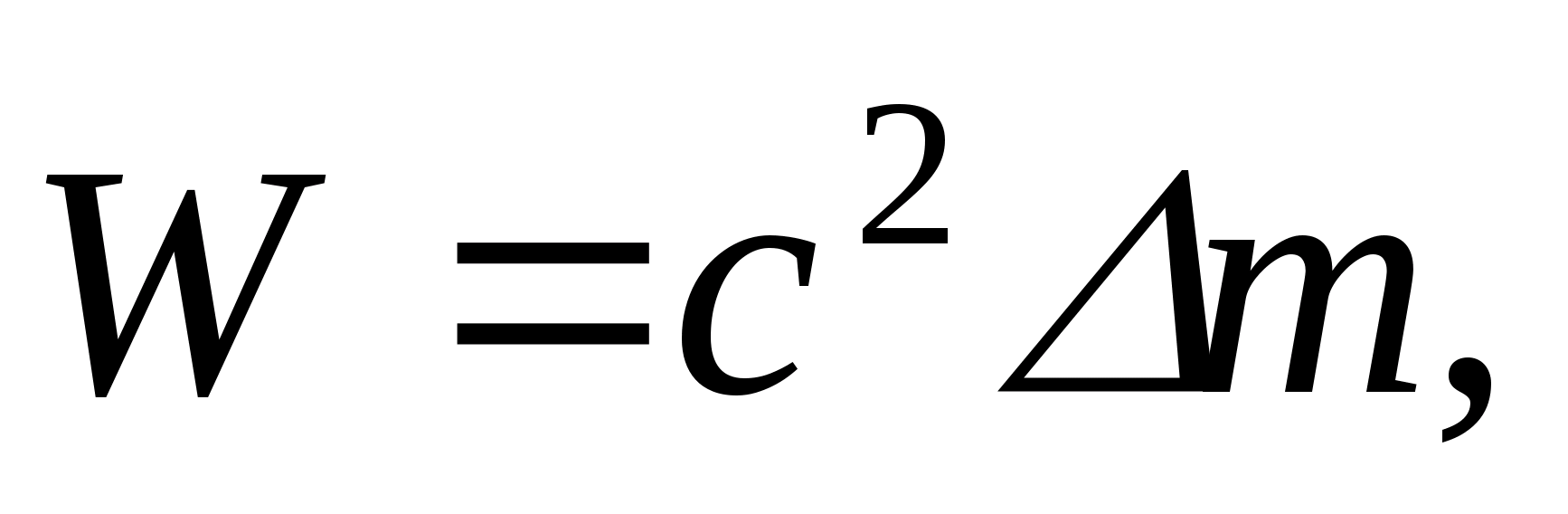(3)

Where With– speed of light in vacuum.

Proportionality factor With 2 can be expressed in two ways: or

If we calculate the binding energy using extra-systemic units, then

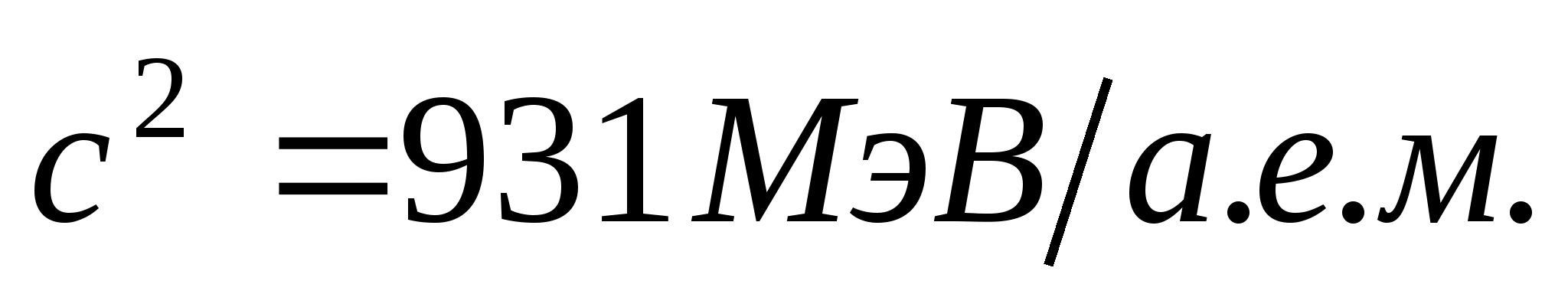
Taking this into account, formula (3) will take the form

(4)

Substituting the previously found value of the core mass defect into formula (4), we obtain

3. Two elementary particles - a proton and an antiproton, having a mass of

Each kg, when combined, turns into two gamma quanta. How much energy is released in this case?

Solution. Finding the gamma quantum energy using Einstein's formula

, where c is the speed of light in vacuum.

4. Determine the energy required to separate a 10 Ne 20 nucleus into a carbon nucleus 6 C 12 and two alpha particles, if it is known that the specific binding energies in 10 Ne 20 nuclei; 6 C 12 and 2 He 4 are respectively equal: 8.03; 7.68 and 7.07 MeV per nucleon.

Solution. During the formation of the 10 Ne 20 nucleus, energy would be released from free nucleons:

W Ne = W c y ·A = 8.03 20 = 160.6 MeV.

Accordingly, for a 6 12 C nucleus and two 2 4 He nuclei:

W c = 7.68 12 = 92.16 MeV,

WHe = 7.07·8 = 56.56 MeV.

Then, during the formation of 10 20 Ne from two 2 4 He nuclei and a 6 12 C nucleus, energy would be released:

W = W Ne – W c – W He

W= 160.6 – 92.16 – 56.56 = 11.88 MeV.

The same energy must be spent on the process of dividing the 10 20 Ne nucleus into 6 12 C and 2 2 4 H.

Answer. E = 11.88 MeV.

5 . Find the binding energy of the nucleus of the aluminum atom 13 Al 27, find the specific binding energy.

Solution. The 13 Al 27 nucleus consists of Z=13 protons and

A-Z = 27 - 13 neutrons.

The core mass is

m i = m at - Z·m e = 27/6.02·10 26 -13·9.1·10 -31 = 4.484·10 -26 kg=

27.012 amu

The core mass defect is equal to ∆m = Z m p + (A-Z) m n - m i

Numerical value

∆m = 13·1.00759 + 14×1.00899 - 26.99010 = 0.23443 amu

Binding energy Wst = 931.5 ∆m = 931.5 0.23443 = 218.37 MeV

Specific binding energy Wsp = 218.37/27 = 8.08 MeV/nucleon.

Answer: binding energy Wb = 218.37 MeV; specific energy connection Wsp = 8.08 MeV/nucleon.

16. Nuclear reactions

Nuclear reactions are the processes of transformation atomic nuclei, caused by their interaction with each other or with elementary particles.

When writing a nuclear reaction, the sum of the initial particles is written on the left, then an arrow is placed, followed by the sum of the final products. For example,

The same reaction can be written in a shorter symbolic form

When considering nuclear reactions, precise conservation laws: energy, impulse, angular momentum, electric charge and others. If as elementary particles In a nuclear reaction, only neutrons, protons and γ quanta appear, then during the reaction the number of nucleons is also preserved. Then the balance of neutrons and the balance of protons in the initial and final states must be observed. For reaction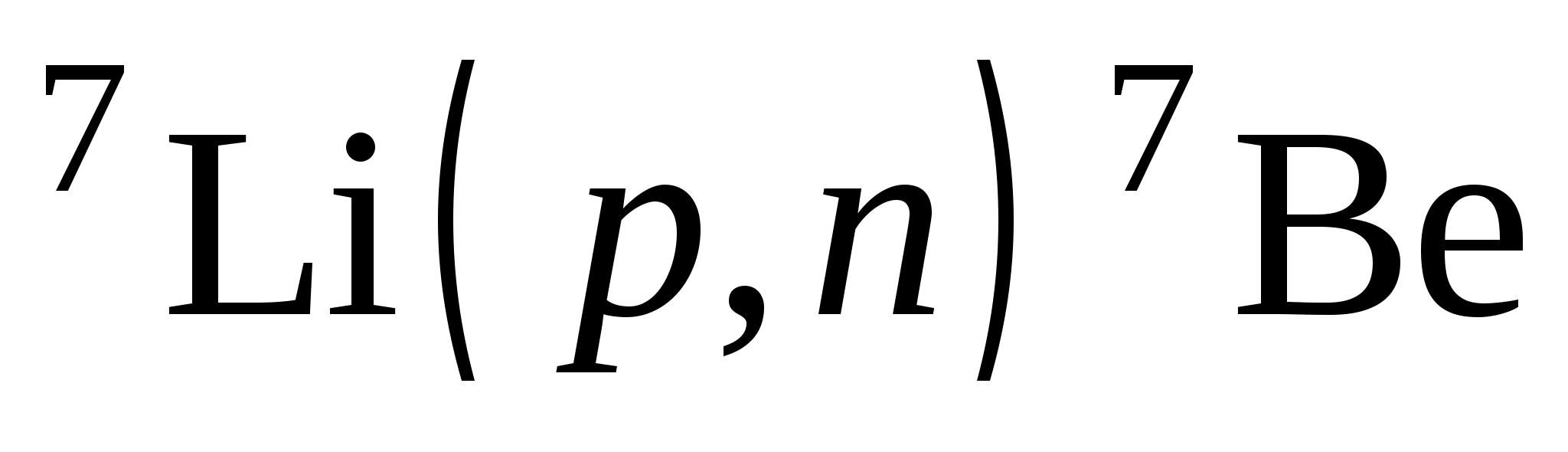

we get:

Number of protons 3 + 1 = 0 + 4;

Number of neutrons 4 + 0 = 1 + 3.

Using this rule, you can identify one of the participants in the reaction, knowing the others. Quite frequent participants in nuclear reactions are α – particles (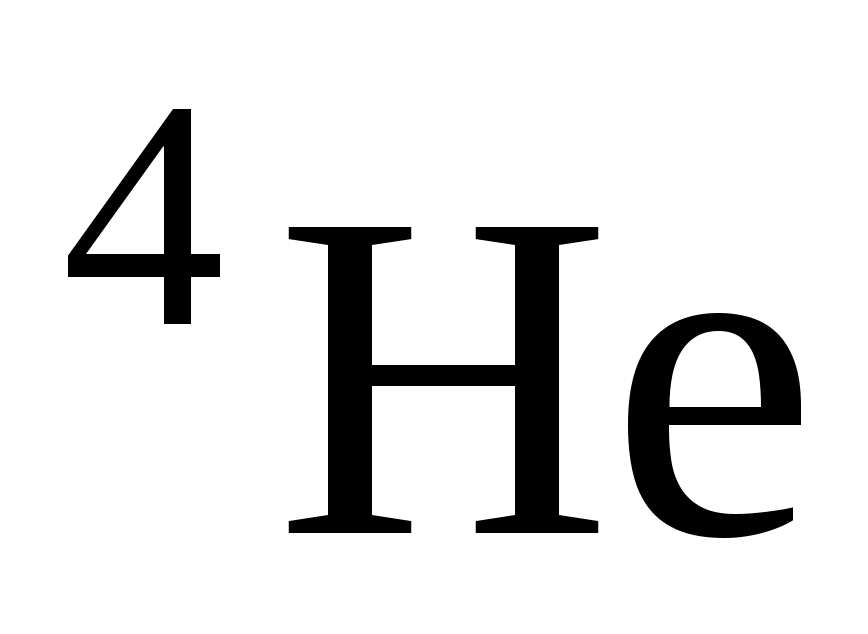

- helium nuclei), deuterons (

- nuclei of a heavy isotope of hydrogen, containing in addition to the proton one neutron) and tritons (

- nuclei of a superheavy isotope of hydrogen containing, in addition to a proton, two neutrons).

The difference between the rest energies of the initial and final particles determines the energy of the reaction. It can be either greater than zero or less than zero. In a more complete form, the reaction discussed above is written as follows:

Where Q– reaction energy. To calculate it using tables of nuclear properties, compare the difference between the total mass of the initial participants in the reaction and the total mass of the reaction products. The resulting mass difference (usually expressed in amu) is then converted into energy units (1 amu corresponds to 931.5 MeV).

17. Examples of problem solving

1. Determine the unknown element formed during the bombardment of aluminum isotope nuclei Al-particles, if it is known that one of the reaction products is a neutron.

Solution. Let's write down the nuclear reaction:

Al+ 

X+n.

According to the law of conservation of mass numbers: 27+4 = A+1. Hence the mass number of the unknown element A = 30. Similarly, according to the law of conservation of charges 13+2 = Z+0 And Z = 15.

From the periodic table we find that this is an isotope of phosphorus R.

2. What nuclear reaction is written by the equation

?

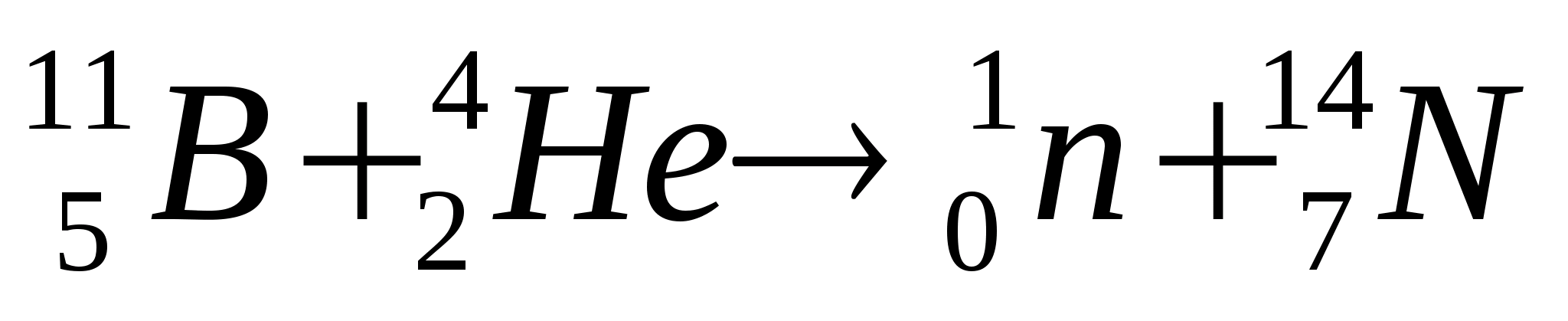Solution. The numbers next to the symbol of a chemical element mean: below is the number of this chemical element in D.I. Mendeleev’s table (or the charge of a given particle), and at the top is the mass number, i.e. the number of nucleons in the nucleus (protons and neutrons together). According to the periodic table, we notice that the element boron B is in fifth place, helium He is in second place, and nitrogen N is in seventh place. Particle 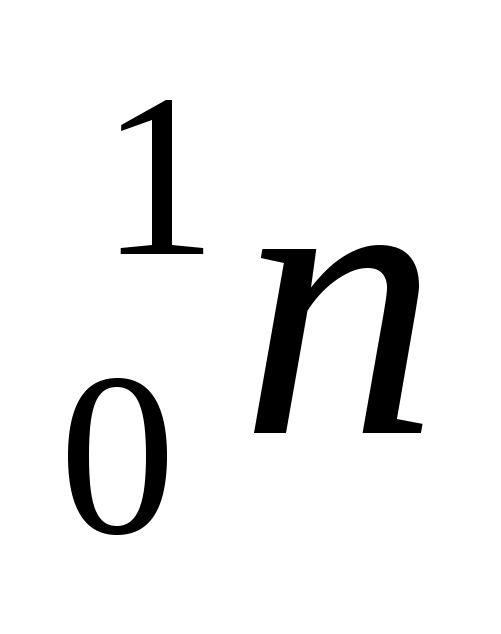- neutron. This means that the reaction can be read as follows: the nucleus of a boron atom with mass number 11 (boron-11) after capture

- particles (one nucleus of a helium atom) emits a neutron and turns into the nucleus of a nitrogen atom with a mass number of 14 (nitrogen-14).

3. When irradiating aluminum nuclei – 27 hard – magnesium nuclei are formed by quanta – 26. Which particle is released in this reaction? Write the equation for the nuclear reaction.

Solution.

According to the law of conservation of charge: 13+0=12+Z;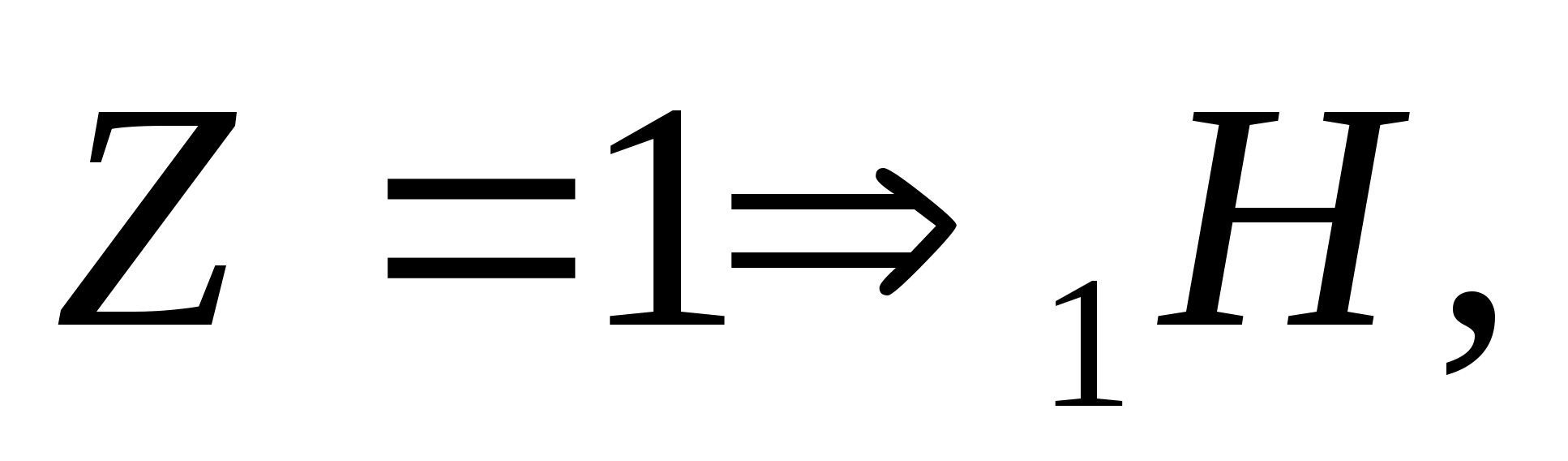

4. When the nuclei of a certain chemical element are irradiated with protons, sodium nuclei are formed - 22 and - particles (one for each act of transformation). Which nuclei were irradiated? Write the equation for the nuclear reaction.

Solution. According to the periodic system chemical elements D.I. Mendeleev:

According to the law of conservation of charge:

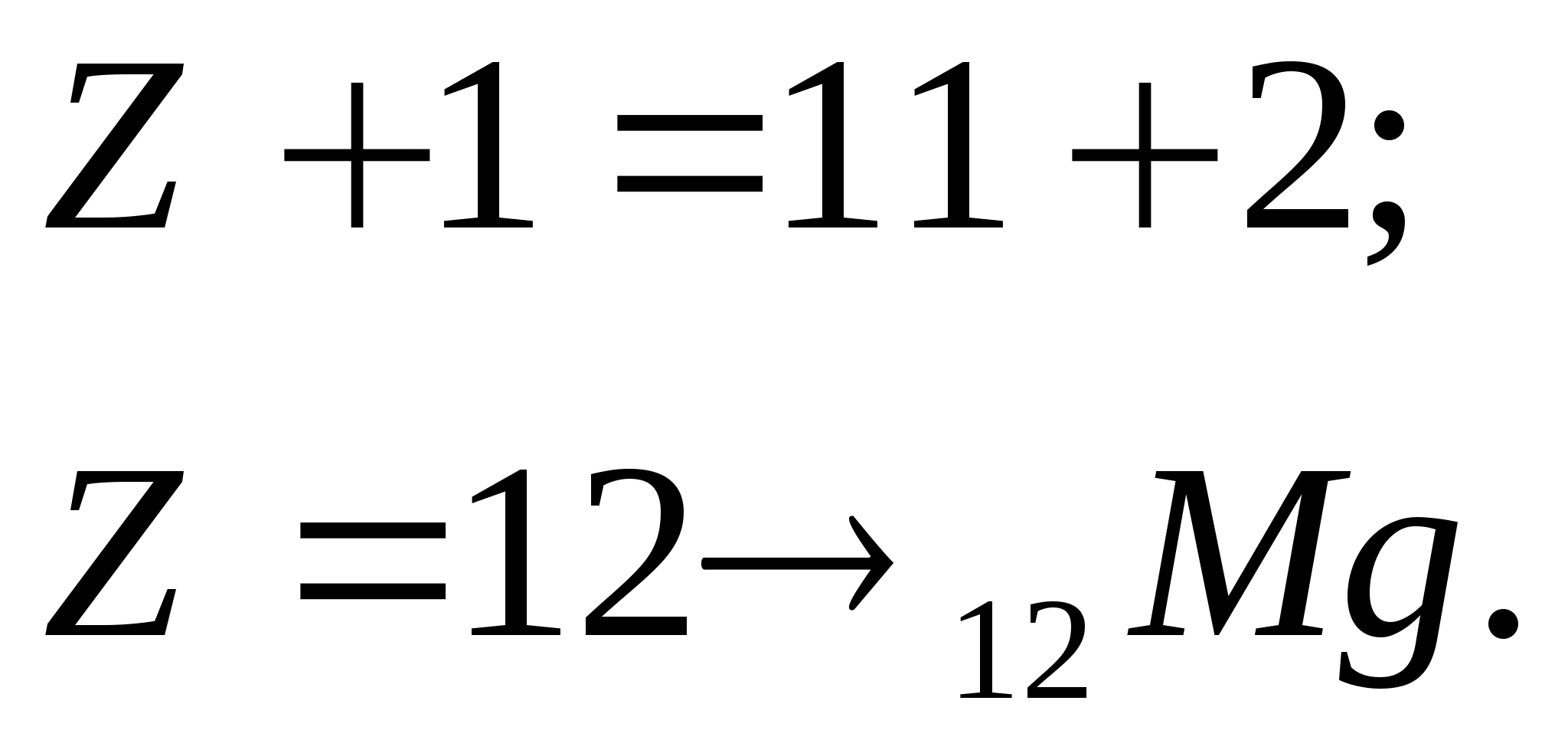
According to the law of conservation of mass number:

5 . When the nitrogen isotope 7 N 14 is bombarded with neutrons, the carbon isotope 6 C 14 is obtained, which turns out to be β-radioactive. Write equations for both reactions.

Solution . 7 N 14 + 0 n 1 → 6 C 14 + 1 H 1 ; 6 C 14 → -1 e 0 + 7 N 14 .

6. The stable decay product of 40 Zr 97 is 42 Mo 97. As a result of what radioactive transformations of 40 Zr 97 is it formed?

Solution. Let us write two β-decay reactions occurring sequentially:

1) 40 Zr 97 →β→ 41 X 97 + -1 e 0, X ≡ 41 Nb 97 (niobium),

2) 41 Nb 97 →β→ 42 Y 97 + -1 e 0, Y ≡ 42 Mo 97 (molybdenum).

Answer : As a result of two β-decays, a molybdenum atom is formed from a zirconium atom.

18. Nuclear reaction energy

Energy of a nuclear reaction (or thermal effect of a reaction)

Where

- the sum of particle masses before the reaction,

- the sum of the particle masses after the reaction.

If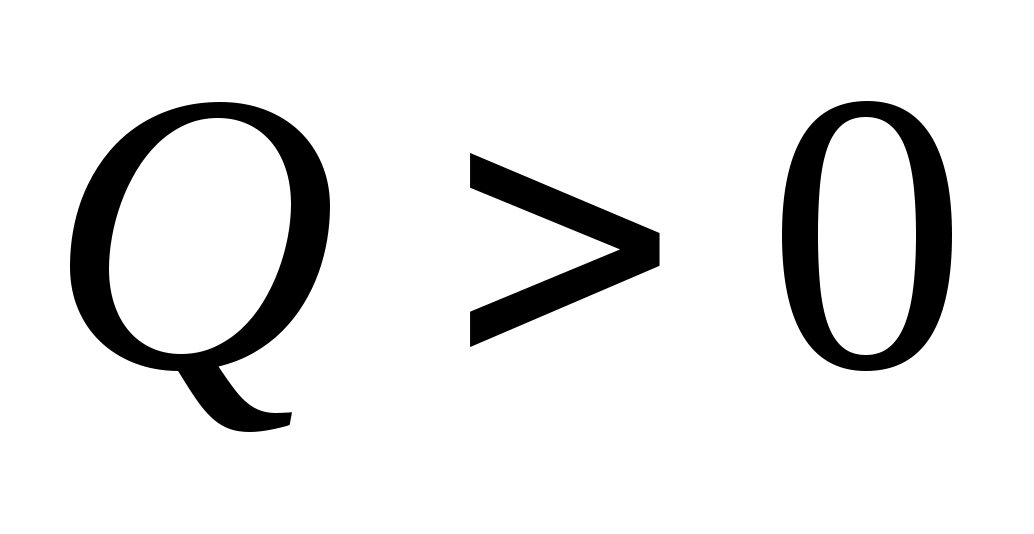

, the reaction is called exoenergetic, since it occurs with the release of energy. At Q < 0 реакция называется эндоэнергетической и для ее возбуждения необходимо затратить энергию (например, ускорить частицы, т.е. сообщить им достаточную кинетическую энергию).

Nuclear fission by neutrons – exoenergetic reaction , in which the nucleus, capturing a neutron, splits into two (occasionally into three) for the most part unequal radioactive fragments, emitting at the same time gamma quanta and 2 - 3 neutrons. These neutrons, if there is enough fissile material around, can in turn cause the surrounding nuclei to fission. In this case, there is chain reaction, accompanied by release large quantity energy. Energy is released due to the fact that the fissile nucleus has either a very small mass defect, or even an excess of mass instead of a defect, which is the reason for the instability of such nuclei with respect to fission.

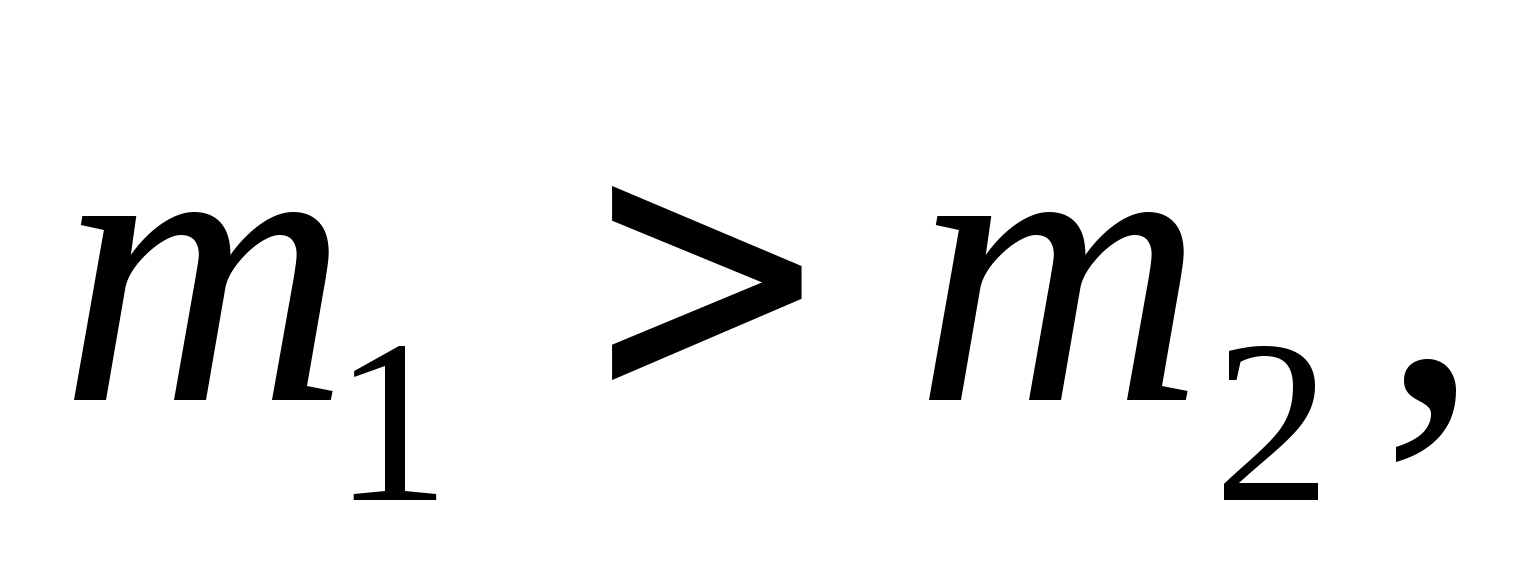energy is released

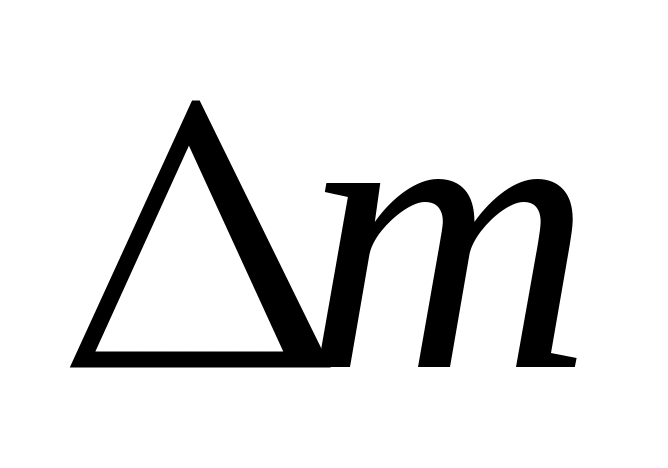=- 0.00352 a.m.u.

3. When a uranium nucleus fissions - 235, as a result of the capture of a slow neutron, fragments are formed: xenon - 139 and strontium - 94. Three neutrons are released simultaneously. Find the energy released during one act of fission.

Solution. Obviously, when dividing the sum atomic masses the resulting particles are less than the sum of the masses of the initial particles by an amount

Assuming that all the energy released during fission is converted into the kinetic energy of the fragments, we obtain after substituting numerical values:

4. What amount of energy is released as a result of the thermonuclear reaction of fusion of 1 g of helium from deuterium and tritium?

fission reaction of heavy nuclei, For example

In this reaction, neutron multiplication is observed. The most important quantity is neutron multiplication factor k . It is equal to the ratio of the total number of neutrons in any generation to the one that gave birth to them total number neutrons in the previous generation. Thus, if in the first generation there was N 1 neutrons, then their number in nth generation will

N n = N 1 k n .

At k=1 The fission reaction is stationary, i.e. the number of neutrons in all generations is the same - there is no multiplication of neutrons. The corresponding state of the reactor is called critical.

At k>1 the formation of an uncontrollable avalanche-like chain reaction is possible, which is what happens in atomic bombs. In nuclear power plants, a controlled reaction is maintained, in which, due to graphite absorbers, the number of neutrons is maintained at a certain constant level.

Possible nuclear fusion reactions or thermonuclear reactions, when two light nuclei form one heavier nucleus. For example, the synthesis of nuclei of hydrogen isotopes - deuterium and tritium and the formation of a helium nucleus:

In this case, 17.6 is released MeV energy, which is about four times more per nucleon than in a nuclear fission reaction. The synthesis reaction occurs in explosions hydrogen bombs. For more than 40 years, scientists have been working to implement a controlled thermonuclear reaction, which would give humanity access to an inexhaustible “storehouse” of nuclear energy.

21. Biological effects of radioactive radiation

Radiation from radioactive substances has a very strong effect on all living organisms. Even relatively weak radiation, which, when completely absorbed, increases body temperature by only 0.00 1 ° C, disrupts the vital activity of cells.

A living cell is a complex mechanism that is not capable of continuing normal activity even with minor damage to its individual parts. Meanwhile, even weak radiation can cause significant damage to cells and cause dangerous diseases (radiation sickness). At high radiation intensity, living organisms die. The danger of radiation is aggravated by the fact that it does not cause any pain even at lethal doses.

The mechanism of radiation affecting biological objects has not yet been sufficiently studied. But it is clear that it comes down to the ionization of atoms and molecules and this leads to a change in their chemical activity. The nuclei of cells are most sensitive to radiation, especially cells that divide rapidly. Therefore, first of all, radiation affects the bone marrow, which disrupts the process of blood formation. Next comes damage to the cells of the digestive tract and other organs.

Radiation has a strong influence on heredity. In most cases, this effect is unfavorable.

Irradiation of living organisms can also have certain benefits. Rapidly multiplying cells in malignant (cancerous) tumors are more sensitive to radiation than normal cells. This is the basis for the suppression of a cancer tumor by -rays of radioactive drugs, which for this purpose are more effective than x-rays.

1. General properties of atomic nuclei. Rutherford's experiments established the existence of atomic nuclei. The atomic nucleus of each element has certain properties that determine: electric charge, mass, electric and magnetic moments, spin, etc. Core charge. Electric charge atomic nucleus is positive. Its value is determined by the product Ze, where Z is the atomic number of the element equal to the serial number in the periodic system of D.I. Mendeleev, e is the elementary charge equal to 1.6022 1019 C. The electric charge determines the number of protons in the nucleus and the number of electrons in a neutral atom, the nature of the intra-atomic electric field, on which the physical and chemical properties of atoms depend. The mass of the nucleus is its second important characteristic. In practice, the mass of the atomic nucleus coincides with the mass of the atom, since the mass of the electrons that make up the atom is very insignificant. The mass of atoms can be determined by the deviation of their ions in electrical and magnetic fields. Atoms whose nuclei have the same charges but different masses are called isotopes.

Sizes and shape of kernels. Certain information about the size and shape of a nucleus can be obtained by studying its electric field, which is studied by the method of scattering charged particles on nuclei. The study of the electric field of the nucleus allowed us to draw a conclusion about its shape. So, in the case of a spherically symmetric nucleus, its field should also be spherically symmetric, that is, the same as the field point charge. The studies have shown that not all nuclei are spherically symmetrical, but all nuclei, without exception, are characterized by axial symmetry.

The spin of a nucleus, together with its charge and mass, is its the most important characteristic. The spin of a nucleus is called its total mechanical moment, which is the sum of the intrinsic angular momentum of its constituent particles and their orbital mechanical moments caused by intranuclear motions. The spin of the nucleus depends on its state. Therefore, the spin of the nucleus in the ground state is usually assumed. The nuclear spin is determined by the number of hyperfine structure lines during spectroscopic studies. In addition to spin, nuclei have characteristic magnetic moments. The magnetic moments of nuclei are expressed in nuclear magnetons, which are introduced similarly to the Bohr magneton. There is an unambiguous connection between the spin and the statistics of the nucleus. Nuclei with integer spin are subject to Fermi-Dirac statistics, and with integer spin - to Bose-Einstein statistics.

2. Nuclear binding energy. Specific binding energy. The energy that must be expended in order to overcome nuclear forces and split a nucleus into individual nucleons is called binding energy atomic nucleus. As follows from the law of conservation of energy, if a nucleus is formed from individual nucleons, then the binding energy of the nucleus at the moment of its formation is released in the form of radiation. From the law of the relationship between mass and energy it follows that E St. =Dm·c 2 , Where Dm-nucleus mass defect.

Let's calculate the total rest mass of nucleons entering the nucleus of any element: (Z·m p +(A-Z)·m n). Let's compare the resulting number with the mass of the nucleus M i. It turned out that for all elements of the periodic table the mass of the nucleus is less than the total mass of the particles that make up the nucleus. The difference between these values ​​is called the mass defect:

Dm=Z m p +(A-Z) m n -M I

So, the formula by which you can calculate the binding energy is:

E St. =(Z m p +(A-Z) m n -M I )·c 2

The binding energy per nucleon is called specific energy communications: dE=DE/A

In Fig. Figure 20 shows a graph of specific binding energy versus mass number. Analyzing this graph, we can draw the following conclusions:

1. Specific binding energy is not a constant value for different nuclei, i.e. The bond strength of nucleons in different nuclei is different. The nucleons are most tightly bound in nuclei with mass numbers in the range of approximately 40 to 100. For this group of nuclei, the specific binding energy is approximately 8.7 MeV/nucleon.

2. The specific binding energy of nuclei with mass number A > 100 decreases and for uranium is 7.6 MeV.

3. In light nuclei, the specific binding energy decreases with decreasing number of nucleons in the nucleus. A characteristic feature of the specific binding energy curve in this group of nuclei is the presence of sharp maxima and minima. The maximum value of the specific binding energy falls on the nuclei and the minimum value falls on the nuclei

3. Weizsäcker formula for binding energy.

Bond energy:

E St =c 2. (1)

It is more convenient to use the following notation (accurate to the electron binding energy):

Let us consider the ratio of the binding energy of the nucleus to the mass number

By definition, ε is average binding energy, per one nucleon ( specific binding energy nucleon in the nucleus). Thus, it characterizes the intensity of nuclear forces. As can be seen from Fig. 1, at small values ​​of mass numbers ε increases sharply and reaches a maximum at A ≈ 5060 (about 8.38.8 MeV). Nuclides with such mass numbers are the most stable. With further growth of A, the average binding energy decreases, however, over a wide range of mass numbers, the value of the specific binding energy is almost constant (=8 MeV). From the above it follows that we can write (3)

It is not difficult to understand that if each nucleon of the nucleus interacted with (A– 1) other nucleons, then total energy of this interaction would be proportional to the product A(A – 1) ≈ A. The difference between this relationship and (3) indicates the property of saturation of nuclear forces: each nucleon in the nucleus interacts not with all the others, but only with a limited number of neighboring nucleons. Nuclear forces are attractive forces, and, as evidenced by the existence of stable nuclei, under some conditions they are greater than the Coulomb repulsion forces (the Coulomb repulsion energy of two neighboring protons in a nucleus is an order of magnitude less than the attractive energy).

Dependence of the average binding energy ε per nucleon on the mass number

Fig.1

The release of energy in nuclear fusion or fission reactions is due to an increase in ε during the fusion of the lightest nuclei into heavier ones or during the fission of heavy nuclei. Local maxima of the ε(A) curve are associated with the formation of stable nuclear shells.

The form of the dependence of the binding energy on the mass number led to the idea of ​​an analogy between a nucleus and a drop of liquid, which led to the creation of a droplet model of the nucleus and the obtaining of a semi-empirical Weizsäcker formulas for the nuclear binding energy.

,

where a 1 = 15.75 MeV; a 2 = 17.8 MeV; a 3 = 0.71 MeV; a 4 = 23.7 MeV; │δ│ = 34 A -3/4. The first term determines the proportionality of the binding energy of the nucleus and the mass of the nucleus, the equivalence of the nucleons of the nucleus and the interaction of each of them only with nearby neighbors. The second term takes into account the fact that nucleons on the surface of the nucleus interact with a smaller number of other nucleons and are thus bound to them less strongly (evaporation of the molecules of a liquid drop occurs from its surface). This leads to a decrease in the binding energy of the nucleus. The total number of “surface” nucleons is proportional to R 2 ~ A 2/3. The third term takes into account the presence of Coulomb repulsion forces between protons (ΔE coul ~ Z(Z – 1)/R ≈ Z 2 /R ~ Z 2 /A 1/3). The fourth term takes into account the presence of proton-neutron asymmetry (presence of spin). The fifth term takes into account the influence of the parity of Z and A – Z on the stability of nuclei: for even-even nuclei (even A and even Z) is substituted into the formula +│δ│; for odd-odd nuclei (even A and odd Z) is substituted into the formula -│δ│; for odd-even and even-odd kernels (all other options), 0 is substituted into the Weizsäcker formula.

4. Weizsäcker formula for core mass.

We list the main characteristics of the cores, which will be discussed further:

1. Binding energy and nuclear mass.
2. Kernel sizes.
3. Nuclear spin and angular momentum of the nucleons that make up the nucleus.
4. Parity of the nucleus and particles.
5. Isospin of the nucleus and nucleons.
6. Spectra of nuclei. Characteristics of the ground and excited states.
7. Electromagnetic properties of the nucleus and nucleons.

1. Binding energies and nuclear masses

The mass of stable nuclei is less than the sum of the masses of the nucleons included in the nucleus; the difference between these values ​​determines the binding energy of the nucleus:

(1.7)

The coefficients in (1.7) are selected from the conditions for the best agreement between the model distribution curve and the experimental data. Since such a procedure can be carried out in different ways, there are several sets of Weizsäcker formula coefficients. The following are often used in (1.7):

a 1 = 15.6 MeV, a 2 = 17.2 MeV, a 3 = 0.72 MeV, a 4 = 23.6 MeV,

It is easy to estimate the value of the charge number Z at which nuclei become unstable with respect to spontaneous decay.
Spontaneous nuclear decay occurs when the Coulomb repulsion of nuclear protons begins to dominate over the nuclear forces pulling the nucleus together. An assessment of the nuclear parameters at which such a situation occurs can be made by considering changes in the surface and Coulomb energies during nuclear deformation. If the deformation leads to a more favorable energetic state, the nucleus will spontaneously deform until it divides into two fragments. Quantitatively, such an assessment can be carried out as follows.
During deformation, the core, without changing its volume, turns into an ellipsoid with axes (see Fig. 1.2 ) .

If you buy 5 apples, 200 g each, put them in a bag, and then, after weighing it, you see that you have less than 1 kg of apples, you will, of course, be surprised, but you will not suspect “nature” of deception. You will decide that the seller deceived you, that the apples that you were promised weigh 200 g are actually lighter. But if a physicist, having measured the mass of the nucleus, finds that it is less than the sum of the masses of the nucleons that make up the nucleus, he, too, will not suspect “nature” of deception, he will not even be surprised. He knows that this is due to the interaction between particles.

Rest energy of a composite system equal to the sum of the rest energies of its constituent particles, their kinetic energy and interaction energy. The kinetic energy of the particles that make up the system is less than the energy of their interaction (the latter is negative), otherwise the particles would scatter far from each other. Therefore, the rest energy of a composite system is less than the sum of the rest energies of its constituent particles. So, in accordance with Einstein’s formula

E=mc 2

mass of the composite system is also less than the sum of the masses of its constituent particles. Where does the energy go during formation? connected system? The answer to the form is very simple - it radiates. But if we wanted to describe the radiation process in detail, we would have to turn to complex field theories. Let's return to our apples. Why are we sure that the mass of a bag of apples should be equal to the sum of the masses of all the apples and, of course, the bag? Simply because the apples did not form a bound state.

Core mass m less than the masses of the nucleons that make up the nucleus by the amount Δm, called mass defect:

Δm = Zm p +Nm n — m,

Where m p And m n— masses of proton and neutron.

Energy of communication E NE kernels is the difference between the rest energies of the nucleus and the nucleons that make up the nucleus:

ENE =Zm p c 2 + Nm n c 2 — mc 2 = Δmc 2 .

This is exactly the energy that needs to be expended in order to split the nucleus into separate nucleo-clones. For most but the lightest kernels, binding energy is approximately proportional to the number of nucleons in the nucleus, and the specific binding energy

ε SV =E NE /A

is almost constant and amounts to ~6-8 MeV/nucleon. This property is called saturation of nuclear forces. It indicates that a nucleon in a nucleus interacts effectively only with a small number of other nucleons. If each nucleon interacted with all nucleons, then the specific binding energy would be proportional to the number of nucleons in the nucleus A.

Relative nuclear mass defect:

Δm/m =ENE / m p c 2 .

For most nuclei it is ~0.65-0.85%; for light nuclei it is less, for example, for the deuteron it is 0.1%. Material from the site

On this page there is material on the following topics:

Nucleons in nuclei are in states significantly different from their free states. There is a special nuclear (or strong) interaction between them - attraction. This interaction determines the stability of nuclei, despite the electrostatic repulsion of protons.

The mass of a nucleus is always less than the sum of the masses of its nucleons. The reason for this is that when nucleons combine into a nucleus, binding energy nucleons with each other.

The binding energy is equal to the work that must be done to split a nucleus into its constituent nucleons without imparting kinetic energy to them.

The binding energy is found by the formula:

In this expression the quantity is called mass defect, it is equal to the difference between the total mass of all nucleons and the mass of the nucleus:

In practical calculations, instead of the masses of nuclei, the masses of atoms are used and the binding energy is calculated using the formula:

To calculate the binding energy proceed as follows:

§ Find mass values ​​in the reference book in atomic mass units (amu)

§ Find the mass defect using the formula:

§ Find the binding energy in megaelectronvolts (MeV) using the formula: . (7)

The binding energy per nucleon is called specific binding energy:

. (8)

The dependence of the specific binding energy on the mass number has the form of a curve with a maximum, shown in Figure 2. From this dependence it follows that the maximum specific binding energy occurs at mass numbers of 50–60 (i.e. for elements from Cr to Zn). It reaches 8.7 MeV/nucleon. As the mass number increases and decreases, the specific binding energy decreases. This dependence makes it energetically possible for two types of processes to occur.

1. Division of heavy nuclei into lighter ones.

The calculation shows that the division of a nucleus with mass number A = 240 (E st. sp = 7.5 MeV) into two nuclei with mass numbers A = 120 (E st. sp = 8.5 MeV) would lead to the release of energy equal to

DE = (2 × 120 × 8.5 – 240 × 7.5) = 240 MeV

2. Fusion (synthesis) of light nuclei into one heavier nucleus.

For example, the fusion of two heavy hydrogen nuclei into a helium nucleus would release energy 24 MeV.

For comparison: when reacting C + O 2 ® CO 2(coal combustion) energy is released » 5 eV.

So, nuclei with values ​​A=50÷60 are the most stable.

Why are other kernels also stable? The reason is this. To divide a heavy nucleus into lighter ones, it must go through several intermediate states. Their energy exceeds the energy of the ground state of the nucleus. Therefore, the process of nuclear fission requires additional energy (activation energy). Under normal conditions, nuclei do not receive this energy - spontaneous fission does not occur. Activation energy can be imparted to a heavy nucleus by capturing a neutron. The process of fission of uranium or plutonium nuclei under the influence of neutrons underlies the operation of a nuclear reactor and an atomic bomb.

For light nuclei to merge into one nucleus, they must approach each other at a distance ≈10 -15 m. Such rapprochement is prevented by Coulomb repulsive forces. To overcome this repulsion, the nuclei must move at enormous speeds corresponding to the temperature T≈10 9 K.

The process of synthesis of light nuclei is called thermonuclear reaction. This reaction occurs in the depths of stars and the Sun, as well as during explosions of hydrogen bombs.