Признаки существования экстремума. {Первый достаточный признак экстремума. Исследование функций на выпуклость и вогнутость. Точки перегиба

Для нахождения максимумов и минимумов функции можно пользоваться любым из трех достаточных признаков экстремума. Хотя самым распространенным и удобным является первый из них.

Первое достаточное условие экстремума.

Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда

Другими словами:

Алгоритм.

Находим область определения функции.

Находим производную функции на области определения.

Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называют точками возможного экстремума , проходя через эти точки, производная как раз может изменять свой знак).

Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.

Пример. Найти экстремумы функции .
Решение.
Областью определения функции является все множество действительных чисел, кроме x = 2 .
Находим производную:

Нулями числителя являются точки x = -1 и x = 5 , знаменатель обращается в ноль при x = 2 . Отмечаем эти точки на числовой оси

Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x = -2, x = 0, x = 3 и x = 6 .

Следовательно, на интервале производная положительна (на рисунке ставим знак плюс над этим интервалом). Аналогично

Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.

Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.
В точке x = -1 функция непрерывна и производная меняет знак с плюса на минус, следовательно, по первому признаку экстремума, x = -1 – точка максимума, ей соответствуем максимум функции .
В точке x = 5 функция непрерывна и производная меняет знак с минуса на плюс, следовательно, x = -1 – точка минимума, ей соответствуем минимум функции .
Графическая иллюстрация.

Ответ: .

Второй достаточный признак экстремума функции.
Пусть ,

если , то - точка минимума;

если , то - точка максимума.

Как видите, этот признак требует существования производной как минимум до второго порядка в точке .
Пример. Найти экстремумы функции .
Решение.
Начнем с области определения:

Продифференцируем исходную функцию:

Производная обращается в ноль при x = 1 , то есть, это точка возможного экстремума.
Находим вторую производную функции и вычисляем ее значение при x = 1 :Причем,

Точка экстремума функции - это точка области определения функции , в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции .

Определение . Точка x 1 области определения функции f (x ) называется точкой максимума функции , если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f (x 0 ) > f (x 0 + Δx ) x 1 максимум.

Определение . Точка x 2 области определения функции f (x ) называется точкой минимума функции , если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f (x 0 ) < f (x 0 + Δx ) ). В этом случае говорят, что функция имеет в точке x 2 минимум.

Допустим, точка x 1 - точка максимума функции f (x ) . Тогда в интервале до x 1 функция возрастает , поэтому производная функции больше нуля (f "(x ) > 0 ), а в интервале после x 1 функция убывает, следовательно, и производная функции меньше нуля (f "(x ) < 0 ). Тогда в точке x 1

Допустим также, что точка x 2 - точка минимума функции f (x ) . Тогда в интервале до x 2 функция убывает, а производная функции меньше нуля (f "(x ) < 0 ), а в интервале после x 2 функция возрастает, а производная функции больше нуля (f "(x ) > 0 ). В этом случае также в точке x 2 производная функции равна нулю или не существует.

Теорема Ферма (необходимый признак существования экстремума функции) . Если точка x 0 - точка экстремума функции f (x ) , то в этой точке производная функции равна нулю (f "(x ) = 0 ) или не существует.

Определение . Точки, в которых производная функции равна нулю или не существует, называются критическими точками .

Пример 1. Рассмотрим функцию .

В точке x = 0 производная функции равна нулю, следовательно, точка x = 0 является критической точкой. Однако, как видно на графике функции, она возрастает во всей области определения, поэтому точка x = 0 не является точкой экстремума этой функции.

Таким образом, условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести и другие примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Поэтому нужно располагать достаточными признаками , позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно - максимум или минимум.

Теорема (первый достаточный признак существования экстремума функции). Критическая точка x 0 f (x ) , если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с "плюса" на "минус", то точкой максимума, а если с "минуса" на "плюс", то точкой минимума.

Если же вблизи точки x 0 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки x 0 . В этом случае в точке x 0 экстремума нет.

Итак, чтобы определить точки экстремума функции, требуется выполнить следующее :

Найти производную функции.
Приравнять производную нулю и определить критические точки.
Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с "плюса" на "минус", то критическая точка является точкой максимума, а если с "минуса" на "плюс", то точкой минимума.
Вычислить значение функции в точках экстремума.

Пример 2. Найти экстремумы функции .

Решение. Найдём производную функции:

Приравняем производную нулю, чтобы найти критические точки:

Так как для любых значений "икса" знаменатель не равен нулю, то приравняем нулю числитель:

Получили одну критическую точку x = 3 . Определим знак производной в интервалах, разграниченных этой точкой:

в интервале от минус бесконечности до 3 - знак минус, то есть функция убывает,

в интервале от 3 до плюс бесконечности - знак плюс, то есть функция возрастает.

То есть, точка x = 3 является точкой минимума.

Найдём значение функции в точке минимума:

Таким образом, точка экстремума функции найдена: (3; 0) , причём она является точкой минимума.

Теорема (второй достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f (x ) , если вторая производная функции в этой точке не равна нулю (f ""(x ) ≠ 0 ), причём, если вторая производная больше нуля (f ""(x ) > 0 ), то точкой максимума, а если вторая производная меньше нуля (f ""(x ) < 0 ), то точкой минимума.

Замечание 1. Если в точке x 0 обращаются в нуль и первая, и вторая производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума функции.

Замечание 2. Второй достаточный признак экстремума функции неприменим и тогда, когда в стационарной точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно вопользоваться первым достаточным признаком экстремума функции.

Локальный характер экстремумов функции

Из приведённых определений следует, что экстремум функции имеет локальный характер - это наибольшее и наименьшее значение функции по сравнению с близлежайшими значениями.

Предположим, вы рассматриваете свои заработки в отрезке времени протяжённостью в один год. Если в мае вы заработали 45 000 рублей, а в апреле 42 000 рублей и в июне 39 000 рублей, то майский заработок - максимум функции заработка по сравнению с близлежайшими значениями. Но в октябре вы заработали 71 000 рублей, в сентябре 75 000 рублей, а в ноябре 74 000 рублей, поэтому октябрьский заработок - минимум функции заработка по сравнению с близлежашими значениями. И вы легко видите, что максимум среди значений апреля-мая-июня меньше минимума сентября-октября-ноября.

Говоря обобщённо, на промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо максимума. Так, для функции изображённой на рисунке выше, .

То есть не следует думать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на всём рассматриваемом отрезке. В точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума - наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.

Поэтому можно уточнить приведённое выше понятие точек экстремума функции и называть точки минимума точками локального минимума, а точки максимума - точками локального максимума.

Ищем экстремумы функции вместе

Пример 3.

Решение.Функция определена и непрерывна на всей числовой прямой. Её производная существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых , т.е. , откуда и . Критическими точками и разбивают всю область определения функции на три интервала монотонности: . Выберем в каждой из них по одной контрольной точке и найдём знак производной в этой точке.

Для интервала контрольной точкой может служить : находим . Взяв в интервале точку , получим , а взяв в интервале точку , имеем . Итак, в интервалах и , а в интервале . Согласно первому достаточному признаку экстремума, в точке экстремума нет (так как производная сохраняет знак в интервале ), а в точке функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: , а . В интервале функция убывает, так как в этом интервале , а в интервале возрастает, так как в этом интервале .

Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При получим уравнение , корни которого и , т. е. найдены две точки (0; 0) и (4; 0) графика функции. Используя все полученные сведения, строим график (см. в начале примера).

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных .

Пример 4. Найти экстремумы функции и построить её график.

Областью определения функции является вся числовая прямая, кроме точки , т.е. .

Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала .

Находим производную и критические точки функции:

1) ;

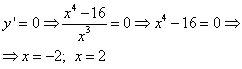2) ,

но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.

Таким образом, заданная функция имеет две критические точки: и . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку . Для этого найдём вторую производную и определим её знак при : получим . Так как и , то является точкой минимума функции, при этом .

Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:

(здесь символом обозначено стремление x к нулю справа, причём x остаётся положительным; аналогично означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если , то . Далее, находим

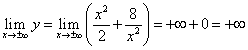т.е. если , то .

Точек пересечения с осями график функции не имеет. Рисунок - в начале примера.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных .

Продолжаем искать экстремумы функции вместе

Пример 8. Найти экстремумы функции .

Решение. Найдём область определения функции. Так как должно выполняться неравенство , то из получаем .

Найдём первую производную функции.

Билет №1

первообразной функцией Теорема Доказательство неопределённым интегралом

Точка (X 0 ;Y 0) называется точкой максимума точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0).

Докозательство:

Билет №2

Доказательство Геометрический смысл

частным приращением частной производной Геометрический смысл

Билет №3

19. Определение точки максимума и минимума функции z=f(x,y). Точка (X 0 ;Y 0) называется точкой максимума функции z=f(x;y), если существует такая δ-окрестность точки (X 0 ;Y 0), что выполняется неравенство f(x;y)точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ><0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №4 Определённым интегралом Свойства Доказательство. в точке с координатами (x;y;z) .Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.Предположим, что функция u(x;y;z) непрерывна и имеет непрерывные производные по своим аргументам в области D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, где E 1 , E 2 , E 3 стремятся к нулю при Δl→0. Разделим всё равенство на Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Равенство можно представить так: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Перейдя к пределу, получим Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Билет №5

1. Первообразная функция. Теорема о разности двух первообразных (с доказательством). Неопределенный интеграл: определение Функция F(x) называется первообразной функцией f(x) на интервале (a;b), если для любого x∈(a;b) выполняется равенство F"(x)=f(x).Теорема . Если функция F(х) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задаётся формулой F(x)+C, где С=const.Доказательство . Функция F(x)+C является первообразной f(x). Действительно, (F(x)+C)"=F"(x)=f(x). Пусть Ф(х) - некоторая другая, отличная от F(x), первообразная функция f(x), т.е. Ф"(х)=f(x). Тогда для любого x∈(a;b) имеем (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x)-f(x)=0. А это означает, что Ф(х)-F(x)=C, C=const. Следовательно, Ф(x)=F(x)+C.Множество всех первообразных функций F(x)+C для f(x) называется неопределённым интегралом от функции f(x) и обозначается символом ∫f(x)dx.

19. Определение точки максимума и минимума функции z=f(x,y). Точка (X 0 ;Y 0) называется точкой максимума функции z=f(x;y), если существует такая δ-окрестность точки (X 0 ;Y 0), что выполняется неравенство f(x;y)точка минимума функции: для всех точек (x;y), отличных от (X 0 ;Y 0), из δ-окрестности точки (X 0 ;Y 0) выполняется неравенство f(x;y)>f(X 0 ;Y 0). 20. Достаточный признак существования экстремума функции z=f(x;y). (формулировка). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ>0, то функция f(x;y) в точке (X 0 ;Y 0) имеет экстремум: максимум, если A<0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №6

3. Вычисление определенного интеграла по отрезку. Формула Ньютона-Лейбница (вывод). Если функция y=f(x) непрерывна на отрезке и F(x) - какая-либо её первообразная на (F"(x)=f(x)), то имеет место формула ∫(от a до b) f(x)dx=F(b)-F(a). Эта формула является формулой Ньютона-Лейбница.Рассмотрим тождество: F(b)-F(a)=F(x n)-F(x 0)=(F(x n)-F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1)-F(x 0)). Преобразуем каждую разность в скобках по формуле Лагранжа: f(b)-f(a)=f’(c)*(b-a). Получим F(b)-F(a)=F’(c n)(x n -x n -1)+F’(c n -1)(x n -1 -x n -2)+F’(c 2)(x 2 -x 1)+F’(c 1)(x 1 -x 0)= ΣF’(Ci)ΔXi=Σf(Ci)ΔXi, то есть F(b)-F(a)= Σf(Ci)ΔXi, где Ci есть некоторая точка интервала (X i -1 ,X i). Так как функция y=f(x) непрерывна на , то она интегрируема на . Поэтому существует предел интегральной суммы, равной определенному интегралу от f(x) на . Переходя к пределу при λ=maxΔXi→0,получаем F(b)-F(a)=lim Σf(Ci)ΔXi, то есть ∫(от a до b) f(x)dx=F(b)-F(a).

Функция z=f(x;y) называется дифференцируемой

11. Свойство дифференцируемой функции: связь между дифференцируемостью функции z=f(x;y) и непрерывностью функции z=f(x;y) в точке (формулировка, доказательство). Если функция z=f(x;y) дифференцируема в точке М(x;y), то она непрерывна в этой точке, имеет в ней частные производные. Доказательство . Пусть функция у=f(x) дифференцируема в точке х 0 . Дадим в этой точке аргументу приращение Δх. Функция получит приращение Δу. Найдем limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Следовательно, у=f(x) непрерывна в точке х 0 .

Билет №7

Необходимый признак экстремума.

Если непрерывная функция z=z(x,y) имеет в точке P0(x0,y0) экстремум, то все ее частные производные первого порядка в этой точке или равны нулю или не существуют

Докозательство: Частная производная функции z=f(x,y) по x в точке P0(x0,y0) есть производная функции одной переменной φ(x)=f(x,y0) в точке x-x0. Но в этой точке функция φ(x) имеет, очевидно, экстремум. Следовательно, φ’(x0)=0 .Так как φ’(x0)=f’x(x0,y0), то f’x(x0,y0)=0 Аналогично можно показать, что f’y(x0,y0)=0 . Теорема доказана.

Билет №8

6. Теорема о среднем (формулировка, доказательство, геометрический смысл). Если функция f(x) непрерывна на отрезке , то существует точка С∈ такая, что ∫(от a до b) f(x)dx=f(c)*(b-a).Доказательство . По формуле Ньютона-Лейбница имеем ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), где F"(x)=f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F"(c)*(b-a)=f(c)*(b-a).Геометрический смысл . Теорема при f(x)≥0 имеем простой геометрический смысл: значение определенного интеграла равно, при некотором С∈ (a;b), площади прямоугольника с высотой f(c) и основанием b-a. Число f(c)=1/(b-a)∫(от a до b) f(x)dx называется средним значением функции f(x) на отрезке .

8. Частные приращения функции z=f(x;y). Частные производные: определение и их геометрический смысл. Пусть задана функция z=f(х;у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной х приращение ∆х, сохраняя значение переменной у неизменным. Тогда функция z получит приращение, которое назовем частным приращением z по х и обозначим ∆ x z. Итак, ∆ x z=f(x+∆x;y)–f(х;у). Аналогично получаем частное приращение z по у: ∆ y z=f(x;у+∆y)–f(х;у).Если существует предел lim∆x→0(∆ x z/∆x)=lim∆x→0((f(x+∆x;y)-f(x;y))/∆x), то он называется частной производной функции z=f(x;y) в точке М(х;у) по переменной х и обозначается одним из символов: z" x , δz/δx; f" x , δf/δx. Геометрический смысл . Графиком функции z=f(x;y) является некоторая поверхность. График функции z=f(x 0 ;y 0) есть линия пересечения этой поверхности с плоскостью у=у 0 . Исходя из геометрического смысла производной для функции одной переменной, заключаем, что f" x (x 0 ;y 0)=tgα, где α - угол между осью Ох и касательной, проведённой к кривой z=f(x 0 ;y 0) в точке M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Аналогично f" y (x 0 ;y 0)=tgβ.

Билет №9

Доказательство Геометрический смысл

Касательной плоскостью Нормалью к поверхности

Билет №10

10. Определение дифференцируемой функции z=f(x;y) в точке. Определение полного дифференциала dz и его форма. Функция z=f(x;y) называется дифференцируемой в точке М(х;у), если её полное приращение в этой точке можно представить в виде: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, где α=α(∆x;∆y)→0 и β=β(∆x;∆y)→0 при ∆x→0 и ∆y→0. Главная часть приращения функции z=f(x;y), линейная относительно ∆x и ∆y, называется полным дифференциалом этой функции и обозначается символом dz: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.

Билет №11

4. Определение определённого интеграла по отрезку. Основные свойства определённого интеграла по отрезку (с доказательством одно из них). Определённым интегралом по отрезку от функции f(x) называется предел интегральной суммы Σf(c i)Δx i , если этот предел существует и не зависит ни от деления отрезка на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i .Свойства : 1)Если с - постоянное число и функция f(x) интегрируема на , то ∫(от a до b) с*f(x)dx=с*∫(от a до b) f(x)dx.2)Если функции f 1 (x) b f 2 (x) интегрируемы на , тогда интегрируема на их сумма и ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫(от a до b) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Если функция f(x) интегрируема на и a

10. Определение дифференцируемой функции z=f(x;y) в точке. Функция z=f(x;y) называется дифференцируемой в точке М(х;у), если её полное приращение в этой точке можно представить в виде: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, где α=α(∆x;∆y)→0 и β=β(∆x;∆y)→0 при ∆x→0 и ∆y→0.

12. Свойство дифференцируемой функции: связь между дифференцируемостью функции z=f(x,y) существованием частных производных в точке (формулировка, доказательство). Теорема: Если функция дифференцируема в точке, то в этой точке существуют конечные частные производные, числено равны А и В Дано: Δz=AΔx+ВΔy+0(ρ) Доказать: Ǝ(δz/δx(x 0 ;y 0)=A Доказательство: Дадим x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A+0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Аналогично: Y 0 →Δy, x=x 0 =>Δ y Z. δz/Δy(x 0 ;y 0)=B.

Билет №12

Доказательство

Билет №13

2. Задача о площади криволинейной трапеции, приводящая к понятию определённого интеграла по отрезку. Определение определённого интеграла по отрезку. Пусть на отрезке задана функция y=f(x)≥0. Фигура, ограниченная сверху графиком функции y=f(x), снизу - осью Ох, сбоку прямые x=a и x=b, называется криволинейной трапецией. Найдём площадь этой трапеции. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. C уменьшением всех величин Δx i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимаемся предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ=maxΔx i →0: S=lim n→∞ Sn=lim n→∞(λ→0) Σf(c i)Δx i , то есть S=∫(от a до b) f(x)dx. Итак, определённый интеграл от неопределённой функции численно равен площади криволинейной трапеции.Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка на численные отрезки, ни от выбора точек в них, то число I называется определённым интегралом от функции y=f(x) на отрезке и обозначается ∫(от a до b) f(x)dx. Таким образом, ∫(от a до b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i .

17. Касательная плоскость и нормаль к поверхности (определение). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 . Нормалью к поверхности в точке М называется прямая, проходящая через эту точку перпендикулярно касательной плоскости.

Билет №14

5. Теорема об оценке определённого интеграла по отрезку (формулировка, доказательство, геометрический смысл). Оценка интеграла. Если m и M - соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке , (aДоказательство . Так как для любого x∈ имеем m≤f(x)≤M, то ∫(от a до b) mdx≤ ∫(от a до b) f(x)dx≤∫(от a до b) Mdx. Получаем: m(b-a)≤∫(от a до b) f(x)dx≤M(b-a). Геометрический смысл . Площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть , а высоты равны m и M.

Билет №15

Билет №16

21. Производная функции u=u(x;y;z) по направлению l (определение). Предел LimΔl→0(Δu/Δl) называется производной функции u(x;y;z) по направлению вектора l в точке с координатами (x;y;z).

22. Градиент функции u=u(x;y;z) в точке (определение). Вектор с координатами (δu/δx; δu/δy; δu/δz) называется

Билет №17

7. Интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом (формулировка, доказательство). Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, то есть (∫(от a до x) f(t)dt)" x =f(x). Доказательство . По формуле Ньютона-Лейбница имеем: ∫(от a до x) f(t)dt=F(t)|(от a до x)=F(x)-F(a). Следовательно, (∫(от a до x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Это означает, что определённый интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

полное приращение непрерывной непрерывна

Билет №18

1. Первообразная функция. Теорема о разности двух первообразных (с доказательством). Неопределенный интеграл: определение, простейшие свойства неопределённого интеграла (с доказательством одно из них). Функция F(x) называется первообразной функцией f(x) на интервале (a;b), если для любого x∈(a;b) выполняется равенство F"(x)=f(x).Теорема . Если функция F(х) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задаётся формулой F(x)+C, где С=const.Доказательство . Функция F(x)+C является первообразной f(x). Действительно, (F(x)+C)"=F"(x)=f(x). Пусть Ф(х) - некоторая другая, отличная от F(x), первообразная функция f(x), т.е. Ф"(х)=f(x). Тогда для любого x∈(a;b) имеем (Ф(х)-F(x))"=Ф"(x)-F"(x)=f(x)-f(x)=0. А это означает, что Ф(х)-F(x)=C, C=const. Следовательно, Ф(x)=F(x)+C.Множество всех первообразных функций F(x)+C для f(x) называется неопределённым интегралом от функции f(x) и обозначается символом ∫f(x)dx.Свойства : 1) Дифференциал от неопределённого интеграла равен подынтегральному выражению, а производная неопределённого интеграла равна подынтегральной функции d(∫f(x)dx)=f(x)dx, (∫f(x)dx)"=f(x).d(∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. и (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) Постоянный множитель можно выносить за знак интеграла: ∫af(x)dx=a∫f(x)dx.4) Неопределённый интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx.5) (Инвариантность формулы интегрирования). Если ∫f(x)dx=F(x)+C, то и ∫f(u)du=F(u)+C, где u=φ(x) - произвольная функция, имеющая непрерывную производную.

22. Градиент функции u=u(x;y;z) в точке (определение, свойства). Связь между производной по направлению и градиентом функции (обоснование). Вектор с координатами (δu/δx; δu/δy; δu/δz) называется градиентом функции u=f(x;y;z) и обозначается gradU=(δu/δx; δu/δy; δu/δz). gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Свойства : 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, где u*v - скалярные произведения векторов u и v. Связь . Пусть задана функция u=u(x;y;z) и поле градиентов gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Тогда производная Δu/Δl по направлению некоторого вектора l равняется проекции вектора GradU на вектор l.

Билет №19

4. Определение определённого интеграла по отрезку. Основные свойства определённого интеграла по отрезку (с доказательством одно из них). Определённым интегралом по отрезку от функции f(x) называется предел интегральной суммы Σf(c i)Δx i , если этот предел существует и не зависит ни от деления отрезка на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i .Свойства : 1)Если с - постоянное число и функция f(x) интегрируема на , то ∫(от a до b) с*f(x)dx=с*∫(от a до b) f(x)dx. Доказательство. Составим интегральную сумму для функции с*f(x). Имеем Σс*f(c i)Δx i =с*Σf(c i)Δx i . Тогда lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(от a до b) f(x)dx. Отсюда вытекает, что функция с*f(x) интегрируема на и справедлива формула ∫(от a до b) с*f(x)dx= с*∫(от a до b) f(x)dx.2)Если функции f 1 (x) b f 2 (x) интегрируемы на , тогда интегрируема на их сумма и ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫(от a до b) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Если функция f(x) интегрируема на и a

17. Касательная плоскость и нормаль к поверхности (определение). Теорема о существовании касательной плоскости (формулровка, доказательство). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 .Нормалью к поверхности в точке М называется прямая, проходящая через эту точку перпендикулярно касательной плоскости.Теорема . Если δF/δx; δF/δy; δF/δz определены в окрестности точки Мо и непрерывны в самой точке М 0 и одновременно в нуль не обращаются, то все касательные прямые к линиям на поверхности лежат в одной плоскости. Доказательство . L: система(x=x(t); y=y(t); z=z(t)). Касательная прямая (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (поверхность). F(x(t), y(t), z(t))=0 сложная функция переменной t. пользуемся правилом дифференцируемости сложной функции: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt)+(δF/δz)*(dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+(δF(M 0)/δz)*z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); обозначим n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0)/δz); n⊥g. Поскольку через данную точку можно провести бесконечное множество линий, лежащих на поверхности, а к ним бесконечное множество касательных прямых, следовательно все касательные прямые лежат в одной плоскости.

Билет №20

9. Полное приращение функции z=f(x;y). Непрерывность функции z=f(x;y) в точке (два определения). Пусть задана функция z=f(x;y). Дадим независимой переменной х приращение ∆х, а переменной у приращение ∆у. Тогда полное приращение ∆z функции определяется равенством: ∆z=f(x+∆x;y+∆y)-f(x;y). 1)Функция z=f(х;у) называется непрерывной в точке М 0 (х 0 ;у 0)∈ D(z), если её предел в этой точке совпадает со значением функции в данной точке, т.е. limX→X 0 \Y→Y 0 (f(x;y))= f(x 0 ;y 0). 2)Функция z=f(х;у) непрерывна на множестве, если она непрерывна в каждой точке этого множества

Билет №21

21. Производная функции u=u(x;y;z) по направлению l (определение, формула для вычисления, вывод формулы вычисления). Предел LimΔl→0(Δu/Δl) называется производной функции u(x;y;z) по направлению вектора l в точке с координатами (x;y;z).Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.Предположим, что функция u(x;y;z) непрерывна и имеет непрерывные производные по своим аргументам в области D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+E 1 Δx+E 2 Δy+E 3 Δz, где E 1 , E 2 , E 3 стремятся к нулю при Δl→0. Разделим всё равенство на Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Равенство можно представить так: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Перейдя к пределу, получим Δu/Δl=LimΔl→0(Δ l u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ.

Билет №22

20. Достаточный признак существования экстремума функции z=f(x;y). (формулировка). Пусть в стационарной точке (X 0 ;Y 0) и некоторой её окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (X 0 ;Y 0) значения A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ;Y 0). Обозначим Δ=|AB; BC|=AC-B^2. Тогда: 1)если Δ>0, то функция f(x;y) в точке (X 0 ;Y 0) имеет экстремум: максимум, если A<0; минимум, если A>0; 2)если Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования.

Билет №23

17. Касательная плоскость к поверхности (определение). Касательной плоскостью к поверхности в точке М называется плоскость, проходящая через эту точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку М и любую другую точку М 1 поверхности, стремится к нулю при М стремящимся к М 1 .

18. Уравнения касательной плоскости к поверхности, заданной явно Явно. z=f(x;y) в точке Mo(Xo;Yo;Zo). K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0

Билет №24

Функция y = f(x) называется возрастающей (убывающей ) в некотором интервале, если при x 1 < x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) > f(x 2)).

Если дифференцируемая функция y = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f " (x) > 0

(f " (x) < 0).

Точка x о называется точкой локального максимума (минимума ) функции f(x), если существует окрестность точки x о , для всех точек которой верно неравенство f(x) ≤ f(x о) (f(x) ≥ f(x о)).

Точки максимума и минимума называются точками экстремума , а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума . Если точка x о является точкой экстремума функции f(x), то либо f " (x о) = 0, либо f (x о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x о - критическая точка. Если f " (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную
f " (x) в окрестности точки x о и вторую производную в самой точке x о . Если f " (x о) = 0, >0 ( <0), то точка x о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Исследование условий и построение графиков.

Найти область определения функции

Найти точки пересечения графика с осями координат

Найти интервалы знака постоянства

Исследовать на четность, нечетность

Найти асимптоты графика функции

Найти интервалы монотонности функции

Найти экстремумы функции

Найти интервалы выпуклости и точки перегиба

Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры.

Вертикальная

Вертикальная асимптота - прямая вида при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

[править]Горизонтальная

Горизонтальная асимптота - прямая вида при условии существования предела

[править]Наклонная

Наклонная асимптота - прямая вида при условии существования пределов

Пример наклонной асимптоты

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при , и из выше указанных замечаний следует, что

1. Функция имеет или только одну наклонную асимптоту, или одну вертикальную асимптоту, или одну наклонную и одну вертикальную, или две наклонных, или две вертикальных, либо же вовсе не имеет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

График функции с двумя горизонтальными асимптотами

]Нахождение асимптот

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов

3. Нахождение двух пределов :

если в п. 2.), то , и предел ищется по формуле горизонтальной асимптоты, .

Первый достаточный признак экстремума формулируется на основе изменения знака первой производной при переходе через критическую точку. О втором признаке экстремума речь пойдёт ниже в § 6.4.

Теорема (первый признак экстремума) : Если х 0 – критическая точка функции у= f (x ) и в некоторой окрестности точки х 0 , переходя через неё слева направо, производная меняет знак на противоположный, то х 0 является точкой экстремума. Причём, если знак производной меняется с «+» на «-», то х 0 – точка максимума, а f (x 0 ) – максимум функции, а если производная меняет знак с «-» на «+», то х 0 – точка минимума, а f (x 0 ) – минимум функции.

Рассмотренный экстремум носит локальный (местный) характер и касается некоторой малой окрестности критической точки.

Точки экстремума и точки разрыва делят область определения функции на интервалы монотонности.

Пример 6.3. В примере 6.1. мы нашли критические точки х 1 =0 и х 2 =2.

Выясним, действительно ли в этих точках функция у=2х 3 -6х 2 +1 имеет экстремум. Подставим в её производную
значениях , взятые слева и справа от точки х 1 =0 в достаточно близкой окрестности, например, х=-1 и х=1 . получим . Так как производная меняет знак с «+» на «-», тох 1 =0 – точка максимума, а максимум функции
. Теперь возьмем два значения х=1 их=3 из окрестности другой критической точки х 2 =2 . Уже показано, что
, а
. Так как производная меняет знак с «-» на «+», тох 2 =2 – точка минимума. А минимум функции
.

Чтобы найти наибольшее и наименьшее значение функции непрерывной на отрезке
нужно вычислить её значение во всех критических точках и на концах отрезка, а затем выбрать из них наибольшее и наименьшее .

6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба

График дифференцируемой функции называется выпуклым на интервале, если он расположен ниже любой своей касательной на том интервале; вогнутым (выпуклым вниз) , если он расположен выше любой касательной на интервале .

6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика

а) Необходимые признаки

Если график функции у= f (x ) выпуклый на интервале (a , b ) , то вторая производная
на этом интервале; если график вогнутый на (a , b ) , то
на (a , b ) .

Пусть график функцииу= f (x ) выпуклый (a , b ) (рис.6.3а). Если касательная скользит вдоль выпуклой кривой слева направо, то её угол наклона убывает (
), вместе с тем убывает и угловой коэффициент касательной, а значит, убывает первая производная
на(a , b ) . Но тогда производная первой производной как производная убывающей функции должна быть отрицательной, то есть
на(a , b ) .

Если график функции вогнутый на (a , b ) , то, рассуждая аналогично, видим, что при скольжении касательной вдоль кривой (рис. 6.3б) угол наклона касательной возрастает (
), возрастает вместе с ним и угловой коэффициент, а значит и производная. И тогда производная от производной как возрастающей функции должна быть положительной, то есть
на(a , b ) .

б) Достаточные признаки

Если для функции у= f (x ) во всех точках некоторого интервала будет
, то график функции вогнутый на этом интервале, а если
, то выпуклый .

«Правило дождя» : Чтобы запомнить какой знак второй производной связывать с выпуклой, а какой с вогнутой дугой графика, рекомендуем запомнить: «плюс вода» в вогнутой луночке, «минус вода» - в выпуклой луночке (рис. 6.4).

Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба .

Теорема (достаточный признак существования точки перегиба).

Если в точке функция
дважды дифференцируема и вторая производная в этой точке равна нулю или не существует, и если при переходе через точкувторая производная
меняет знак, то точкаесть точка перегиба. Координаты точки перегиба
.

Точки, в которых вторая производная обращается в нуль или не существует, называются критическими точками второго рода.

Пример 6.4. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривой
(кривая Гаусса).

Решение. Находим первую и вторую производные:
,. Вторая производная существует при любых. Приравниваем ее нулю и решим полученное уравнение
, где
, тогда
, откуда
,
- критические точки второго рода. Проверим смену знака второй производной при переходе через критическую точку
. Если
, например,
, то
, а если
, например,
, то
, то есть, вторая производная меняет знак. Следовательно,
- абсцисса точки перегиба, ее координаты
. Ввиду четности функции
, точка
, симметричная точке
, тоже будет точкой перегиба.