Пълнотекстово търсене:

Къде да търсите:

навсякъде
само в заглавие
само в текст

Покажи:

описание
думи в текста
само заглавието

Начало\u003e Резюме\u003e Физика

Въведение ………………………………………………………………… ..... 3

Потокът на електрическото поле. Теорема на Гаус в интегрална форма ……………………………………………………… 4

Появата и развитието на теорията на електромагнитното поле ... ... ... 8

Заключение …………………………………………………………………. 15

Референции ………………………………. 16

въведение

Според съвременните концепции електрическите заряди не действат директно един на друг. Всяко заредено тяло създава електрическо поле в заобикалящото пространство, което оказва влияние върху други заредени тела.

Основното свойство на електрическото поле е въздействието на електрически заряди с някаква сила. Така взаимодействието на заредените тела се извършва не чрез директното им действие един срещу друг, а чрез електрическите полета, обграждащи заредените тела.

За количественото определяне на електрическото поле се въвежда силова характеристика - интензивността на електрическото поле.

Силата на електрическото поле се нарича физическа величина, равна на съотношението на силата, с която полето действа върху положителен изпитван заряд, поставен в дадена точка от пространството на величината на това зареждане:

Силата на електрическото поле е векторна физическа величина. Посоката на вектора Е съвпада на всяка точка в пространството с посоката на силата, действаща върху положителния изпитван заряд.

Силата на електрическото поле, създадена от системата за зареждане в дадена точка в пространството, е равна на векторната сума на силата на електрическото поле, генерирана в една и съща точка от отделните зареждания:

Това свойство на електрическото поле означава, че полето се подчинява на принципа на суперпозиция.

Потокът на електрическото поле. Теорема на Гаус в интегрална форма

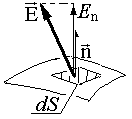
Нека n е нормалната единица към обекта dS (достатъчно малък, за да пренебрегне промяната на електрическата интензивност E в обекта). Потокът dF e на електрическия интензитет през този участък се определя като произведение на нормалната компонента E и dS:

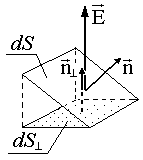
Знакът на потока dF e, очевидно, зависи от взаимната ориентация на нормалната и интензивността. Ако тези два вектора образуват остър ъгъл, потокът е положителен, ако е тъп, той е отрицателен.

Потокът dF e през платформата, наклонена към силовата линия (т.е. към вектора E), също е равен на потока през проекцията на тази област върху равнината, перпендикулярна на линията на сила (виж Фиг. 1.1.2):

Това равенство (1.1.1) следва от дефиницията (1.1.1) за dF e и теоремата за ъгъла с взаимно перпендикулярни страни.

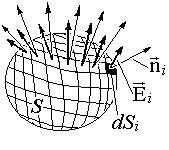
Потокът F e на електрическия интензитет Е през затворената повърхност S (фиг. 1.3.3) се определя като сумата от елементарните потоци през всички повърхностни области. В границата, когато броят на платформите N се стреми към безкрайност, сумата от потоците през платформите преминава в повърхностния интеграл на нормалната компонента на интензитета En:

К. Гаус през 1844 г. доказва теоремата (теорема на Гаус в интегрална форма), която установява връзката между източниците на полето и потока на напрежението през произволна повърхност около източниците.

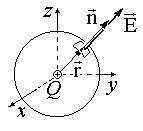
За доказателство извличаме помощна формула. Поток от точково зареждане през произволна околна сфера.

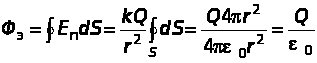. (1.1.4)

Полевите линии на силата на точково зареждане са перпендикулярни на повърхността на концентричната сфера (виж фигура 1.1.4). Като се има предвид този факт, формулата (1.1.4) се извлича от израза за полето на точково натоварване. Както се вижда, в този случай потокът F e не зависи от радиуса на сферата, а зависи само от Q.

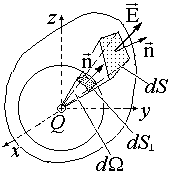
От (1.1.2) и (1.1.4) следва, че полевият поток на точково зареждане през всяка повърхност около заряда е равен на потока през сфера с произволен радиус, концентричен на заряда. В действителност, потока на точково поле на заряда през всяка dS област, изрязана с твърд ъгъл d от произволна повърхност, е същият като потока през областта на сфера, изрязан със същия солиден ъгъл. Потокът на полето F e през сферата, както вече беше отбелязано, не зависи от неговия радиус. Следователно, потокът на силата на полето на точково зарядно в повърхността S (виж фиг. 1.3.5) е даден с формула (1.3.4). От формула (1.3.4) и принципа на суперпозицията следва теоремата на Гаус в интегрална форма: общият поток F e на силата на електрическото поле през произволна затворена повърхност, вътре в която има произволно разпределен (обем, повърхност и т.н.) заряд Q, изчислен от формула

При прилагането на теоремата на Гаус за решаване на проблемите, трябва да се помни, че в уравнение (1.1.5) Q е сумата от всички заряди вътре в умствената повърхност, през която се изчислява потокът, включително таксите, принадлежащи на атоми и молекули на средата (т.нар. Обвързани заряди).

Полевата сила на потока Е през всяка затворена повърхност, в която общият заряд е нула, също е нула.

Появата и развитието на теорията на електромагнитното поле

През 17-ти и 18-ти век електромагнитните процеси проникват по-дълбоко в науката: физика и химия. Започна епохата на електромагнитната картина на света, която замени механичната.

Максуел ясно видя фундаменталното значение на електромагнитните закони, след като извърши грандиозен синтез на оптика и електричество. Той успя да намали оптиката към електромагнетизма, създавайки електромагнитна теория на светлината и проправяйки нови пътища не само в теоретичната физика, но и в технологиите, поставяйки сцена за радиотехника.

Фарадей предприе нов подход към изучаването на електричеството и магнитните явления, посочвайки ролята на средата и въвеждайки концепцията за полето, описано от него, с помощта на силови линии. Максуел дава на идеите математическа пълнота, въвежда точния термин "електромагнитно поле", което Фарадей все още не е имал, формулира математическите закони на това поле. Галилео и Нютон поставят основите на механичната картина на света, Фарадей и Максуел - основите на електромагнитната картина на света.

Максуел развива електромагнитната теория в своите творби „Физически линии на властта” (1861–1862) и теория на динамичното поле (1864–1865). Той пише тези произведения вече не в Абърдийн, а в Лондон, където получава професия в King's College. Тук Максуел се срещна с Фарадей, който вече беше стар и болен. Максуел, получил данни, потвърждаващи електромагнитната природа на светлината, ги изпратил на Фарадей. Максуел пише: „Електромагнитната теория на светлината, предложена от него (Фарадей) в„ Мисли за радиационни вибрации ”(Phil. Mag., May 1846) или„ Експериментални изследвания ”(Exp. Rec., P. 447), е по същество същото нещо, което започнах да развивам в тази статия (“Динамична теория на полето” - Фил. Маг., 1865), с изключение на това, че през 1846 г. нямаше данни за изчисляване на скоростта на разпространение. Dzh.K.M. ".

През 1873 г. Максуел публикува основната си работа - "Трактат за електричеството и магнетизма". Той започва да пише популярна експозиция на своята теория „Електричество в елементарно представяне“, но не е имал време да го довърши.

Максуел е многостранен учен: теоретик, експериментатор, техник. Но в историята на физиката неговото име се свързва предимно с теорията на електромагнитното поле, която той създава, който се нарича теорията на Максуел или електродинамиката на Максуел. Той влезе в историята на науката, заедно с такива фундаментални обобщения като нютоновата механика, релативистката механика, квантовата механика и бележи началото на нов етап във физиката. В съответствие със закона за развитие на науката, формулиран от Аристотел, той издига знанието за природата на ново, по-високо ниво и в същото време е по-неразбираемо, абстрактно от предишните теории, „по-малко очевидно за нас”, според Аристотел.

Максуел започва да развива своята теория през 1854 година.

Максуел характеризира електротоничното състояние с помощта на три функции, които той нарича електротонични функции или компоненти на електротоничното състояние. В съвременната нотация тази векторна функция съответства на потенциалния вектор. Криволинейният интеграл на този вектор по протежение на затворена линия Максуел нарича "общата електротонна интензивност по затворена крива". За това количество той намира първия закон на електротоничното състояние: "Общата електротонна интензивност по границата на повърхностен елемент служи като мярка за количеството магнитна индукция, минаваща през този елемент, или, с други думи, мярка за броя на магнитните линии, проникващи през този елемент." В съвременната нотация този закон може да бъде изразен чрез формулата:

където А е потенциалната векторна компонента в посоката на елемента на кривата dl, Bn е нормалната компонента на индукционния вектор B в посока нормална към повърхностния елемент dS.

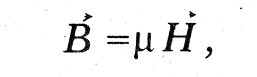
свързваща магнитна индукция В с вектор на интензитета на магнитното поле N.

Третият закон свързва интензивността на магнитното поле H със силата на тока, която го създава. I. Максуел го формулира по следния начин: "Общата магнитна интензивност по линията, ограничаваща всяка част от повърхността, служи като мярка за количеството електрически ток, протичащ през тази повърхност." В съвременната нотация това изречение е описано с формулата

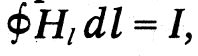
което сега се нарича първото уравнение на Максуел в неразделна форма. Той отразява експериментален факт, открит от Ерстед: токът е заобиколен от магнитно поле.

Четвъртият закон е законът на Ом:

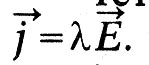
За да характеризира силовите взаимодействия на токовете, Максуел въвежда количество, наречено магнитен потенциал. Тази стойност се подчинява на петия закон: “Общият електромагнитен потенциал на затворен ток се измерва чрез умножаване на количеството ток с общата електротонна интензивност по веригата, изчислена в посока на тока:

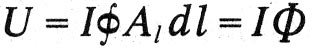
Шестият закон на Максуел е свързан с електромагнитната индукция: "Електроскопичната сила, действаща върху проводящ елемент, се измерва чрез времево производно на електротонната интензивност, независимо от това дали тази дериват е причинена от промяна в магнитуда или посоката на електротоничното състояние." В съвременната нотация този закон се изразява с формулата:

Това е второто уравнение на Максуел в неразделна форма. Отбележете, че електромоторната сила на Максуел се отнася до циркулацията на вектора на интензитета на електрическото поле. Максуел обобщава закона на индукцията на Фарадей - Ленц-Нойман, като се има предвид, че изменението на времето на магнитния поток (електротонично състояние) генерира вихрово електрично поле, което съществува независимо от това дали има затворени проводници, в които това поле възбужда ток или не. Максуел все още не предлага обобщение на закона Ерстед.

Друга важна новина е въвеждането на понятията за токове на пристрастия и пристрастия. Преместването, според Максуел, е характеристика на състоянията на диелектрика в електрическо поле. Общият поток на изместване през затворена повърхност е равен на алгебричната сума на зарядите вътре в повърхността. Това въвежда фундаменталната концепция за ток на пристрастия. Този ток, както и токът на проводимост, създават магнитно поле. Следователно Максуел обобщава уравнението, което сега се нарича първото уравнение на Максуел и въвежда ток на отклонение в първата част. В съвременната нотация това уравнение на Максуел има формата:

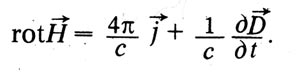
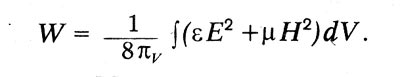
Накрая, Максуел установява, че напречните вълни се разпространяват в неговата еластична среда със скоростта на светлината. Този фундаментален резултат го води до важен извод: “Скоростта на напречните вълнови колебания в нашата хипотетична среда, изчислена от електромагнитните експерименти на Кольраш и Вебер, съвпада точно със скоростта на светлината, изчислена от експериментите на оптичната физика, че трудно можем да откажем заключението, че Светлината се състои от напречни вибрации на същата среда, която е причина за електрически и магнитни явления. Така, в началото на 60-те години на XIX век. Максуел вече беше намерил основата на своята теория за електричеството и магнетизма и направи важното заключение, че светлината е електромагнитно явление.

В теорията на Максуел величината на "електромагнитния момент" е свързана с магнитния поток. Циркулацията на потенциалния вектор по затворена верига е равна на магнитния поток през повърхността, покрита от веригата. Магнитният поток има инерционни свойства, а електромоторната сила на индукцията съгласно правилото на Ленц е пропорционална на скоростта на промяна на магнитния поток, взета с противоположния знак. Оттук и интензивността на индукционното електрическо поле:

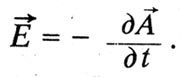
Максуел счита, че този израз е подобен на израза за инерционната сила в механиката:

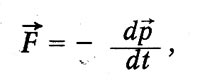
Механичен импулс или количеството движение. Тази аналогия обяснява термина, въведен от Максуел за векторния потенциал. Уравненията на електромагнитно поле в теорията на Максуел имат форма, различна от съвременната.

В съвременна форма системата на Максуел от уравнения има следната форма:

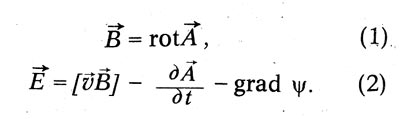
Връзката между вектора на изместване D и силата на електрическото поле Е в Максвел се изразява чрез уравнението:

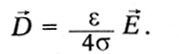
След това записва уравнението divD = p и уравнението където

както и граничното условие:

Такава е системата на уравненията на Максуел. Най-важното заключение от тези уравнения е наличието на напречни електромагнитни вълни, които се разпространяват в намагнитен диелектрик със скорост:

Това заключение е получено от него в последната част от теорията на динамичното поле, наречена Електромагнитна теория на светлината. „... Науката за електромагнетизма - пише Максуел тук - води до същите заключения като оптиката по отношение на посоката на смущенията, която може да се разпространи през полето; И двете науки потвърждават трансверсалността на тези трептения и и двете дават една и съща скорост на разпространение. В етера тази скорост е скоростта на светлината (Максуел означава неговото V), в диелектрика е по-малко къде

По този начин индексът на пречупване п, според Максуел, се определя от електрическите и магнитни свойства на средата. В немагнитен диелектрик, където

Това е известното съотношение на Максуел.

V.Tomson през 1853 г. изследва изтичането на проводник на даден капацитет чрез проводник на дадена форма и съпротива. Прилагайки закона за запазване на енергията в процеса на разреждане, той извлича уравнението на процеса на разреждане в следната форма:

където q е количеството електроенергия на зауствания проводник в даден момент t, C е кондензаторът на проводника, k е галваничното съпротивление на разрядника, A е „константа, която може да се нарече електродинамичен капацитет на разрядника” и сега наричаме коефициент на самоиндукция или индуктивност. Томсън, анализирайки решението на това уравнение за различни корени на характеристичното уравнение, намира това, когато

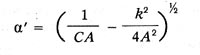
има реална стойност (1 / CA\u003e 4 * (k / A) 2), решението показва, че „главният проводник губи заряда си, зарежда се с по-малко електричество от противоположния знак, отново се изтощава, отново се оказва зареден с още по-малко електричество от оригиналния знак, и това явление се повтаря безкрайно много пъти, докато се установи равновесие. " Цикличната честота на тези затихливи трептения:

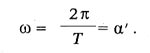
Така периодът на колебание може да бъде представен с формулата:

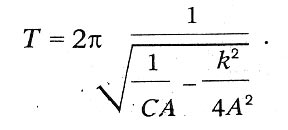
За малки стойности на съпротивление получаваме добре познатата формула Thomson:

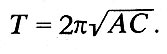
заключение

Електрическото поле е специална форма на поле, която съществува около тела или частици с електрически заряд, както и в свободна форма в електромагнитни вълни. Електрическото поле е директно невидимо, но може да бъде наблюдавано чрез неговото действие и с помощта на инструменти. Основното действие на електрическото поле е ускорението на тела или частици с електрически заряд.

Едно електрическо поле може да се разглежда като математически модел, който описва стойността на силата на електрическото поле в дадена точка в пространството. Дъглас Джанколи пише: „Трябва да се подчертае, че полето не е някаква субстанция, по-точно това е изключително полезно понятие ... Въпросът за„ реалността ”и съществуването на електрическо поле е всъщност философски, по-скоро дори метафизичен въпрос. полето се оказа изключително полезно - това е едно от най-големите постижения на човешкия ум.

Електрическото поле е един от компонентите на едно електромагнитно поле и проявление на електромагнитно взаимодействие.

Позоваването

Дмитриев В.Ф., Прокофьев В.Л. Основи на физиката. - М .: Висше училище, 2003

Калашников Н. П., Смондирев М. А. Основи на физиката. - М .: Дрофа, 2003

Макаров Е. Ф., Озеров Р. П. Физика. - М .: Научен свят, 2002

Савелиев И.В. Курс по обща физика: Учебник. Ръководство: за университети. В 5 kN. Kn.2. Електричество и магнетизъм - 4-то изд., Перераб.- М .: Наука, Физматлит, 2003, сс. 9-30, 41-71

Трофимова Т.И. Курс по физика: Учебник. Ръководство: за университети .- 5-то изд., Старши- М .: Висше. училище, 2003, сс. 148-164

Детлаф А. А., Яворски Б. Курс по физика: Учебник. наръчник за университети - 2-ро издание, Corr. и добави - М .: Висше. училище., 20049, сс. 182-190, 193-202

Електромагнетизъм. Основни закони - 3-то издание, Rev.-M. 6-34

Курсова работа \u003e\u003e Физика

Field. теорема гаус   в интегриран форма   4. Дивергенция на векторно поле. теорема гаус   в диференциал форма   Списък със заключения ... En :. (1.3.3.) гаус   доказано през 1844 година теорема (теорема гаус   в интегриран форма), установяване на връзка между източници ...

Електростатични изследвания

Лаборатория \u003e\u003e Физика

Потенциал. Друга основна връзка е теорема гаус   (В интегриран форма), твърдейки, че е вектор на потока ... на електростатично поле. 11. Дайте определение теорема гаус   в интегриран форма, 12. Дайте определение на потенциала ...

Механика. Молекулярна физика

Резюме \u003e\u003e Физика

Теорема Остроградски, можем да формулираме теорема гаус   за в интегриран форма: векторният поток през ... нула:. - теорема гаус, Използвайки теоремата на Остроградски, получаваме теоремата гаус   за вектор в диференциал форма

В редица раздели на курса по обща физика се разглеждат векторни полета (например електростатично поле, магнитно поле).

При описанието на такива полета често се използва концепцията за векторния поток през повърхността. Помислете за тази концепция.

Нека съществува електрическо поле в даден участък от пространството. Изберете в това поле елементарна зона dS, Нека нормалната в тази област п   образува ъгъл  с вектор на интензитета на електрическото поле (модул на вектор п = 1).

Потокът на вектора на електрическото поле през тази зона се нарича стойност, равна на

където dF   - елементарен поток на вектора на интензивността, E   - вектор на силата на полето в безкрайно малка област гите .

продукт En   е скаларно, следователно потокът на вектора на интензитета е скаларно количество.

Понякога работата п dS   замени с вектор гите който е насочен перпендикулярно на равнината на обекта; вектор модул dS   равно на площта на елементарния обект.

Потокът на напрежение през последната зона ите е

.

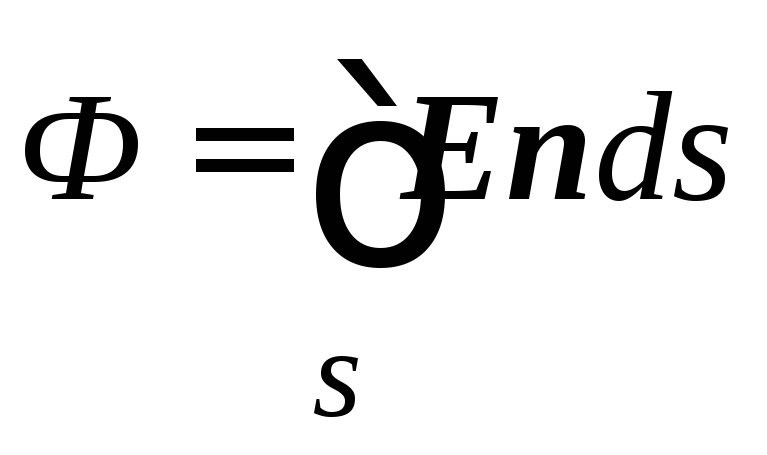В зависимост от ъгъла между нормалното и обекта и вектора E   Потокът може да бъде положителен и отрицателен. Ако ъгълът между векторите E   и п   остър, тогава потокът е положителен, ако е тъп - отрицателен.

Имайте предвид, че посоката на вектора п   се избира произволно преди решаване на проблема (перпендикулярът към повърхността може да бъде насочен към две взаимно противоположни страни). Следователно, знакът на потока на вектора на интензитета се определя от избора на посоката на вектора п.

Ако повърхността е затворена, потокът на вектора на интензитета е

,

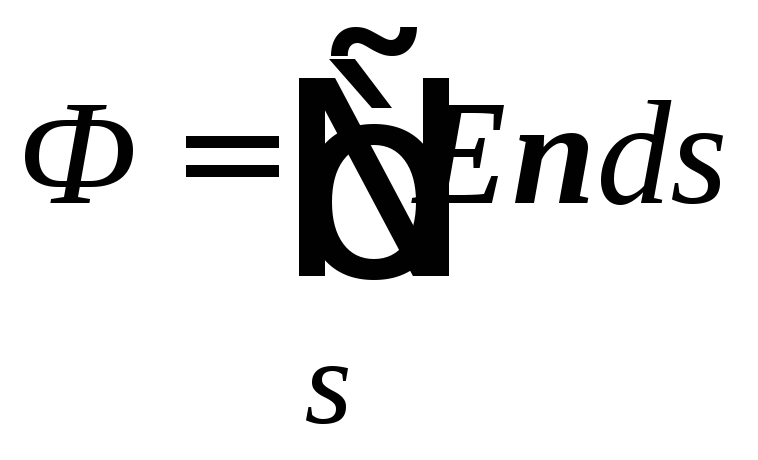т.е. интегралът се поема върху затворена повърхност ите.

В този случай е обичайно да се насочва векторът. п   навън от повърхността. В този случай потокът през затворена повърхност е положителен, ако общият заряд, покрит от затворената повърхност, е положителен.

Размерът на потока на вектора на интензитета [Ф] = В. m = H. m2 / Kl.

1.6. Теорема на Гаус

Теоремата на Гаус е основната теорема за електростатиката. Тя установява връзка между потока на вектора на интензитета през затворена повърхност и общия заряд, обвит от тази повърхност.

Разгледайте тази теорема.

Нека електрическото поле се създава от положителна заряда. р.

Намерете потока на вектора на силата на електрическото поле през затворена повърхност, покриваща този заряд.

Като повърхност, изберете сфера от радиус rчийто център съвпада с таксата р.

Тъй като зарядът създава полето е положителен и се намира в центъра на сферата, ъгълът между вектора E   и вектор п   във всички точки на повърхността е нула.

Следователно, потока на вектора на интензивността през елементарната повърхност dS   ще бъде равен En dS = Ecos dS = Ecos0 dS = Изд.

С други думи, в разглежданата ситуация скаларният продукт на силата на електростатичното поле от елементарния повърхностен вектор е произведението на модулите на тези вектори.

Силата на полето, създадено от зарядното зареждане, е равно на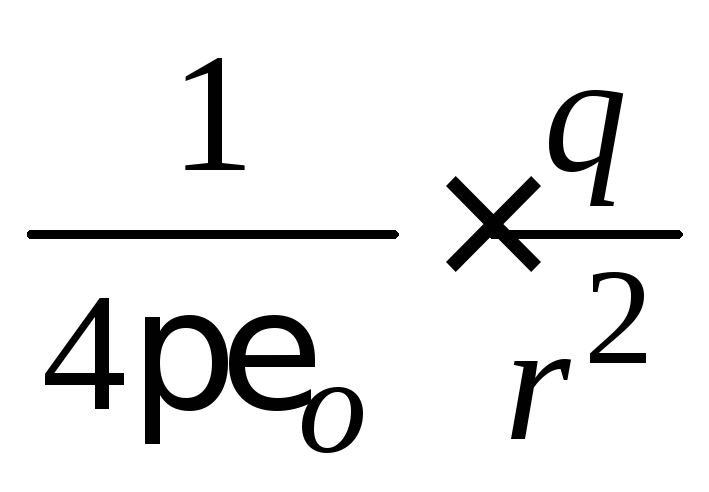

.

Тъй като зарядът е разположен в центъра на сферичната повърхност, разстоянието от заряда до повърхността при всичките му точки е еднакво и равно r, Следователно величината на вектора на якостта във всички точки на сферична повърхност е една и съща: E   = const.

Константата може да се извади от интегралния знак, следователно потокът на вектора на интензитета през затворена повърхност в този случай е равен на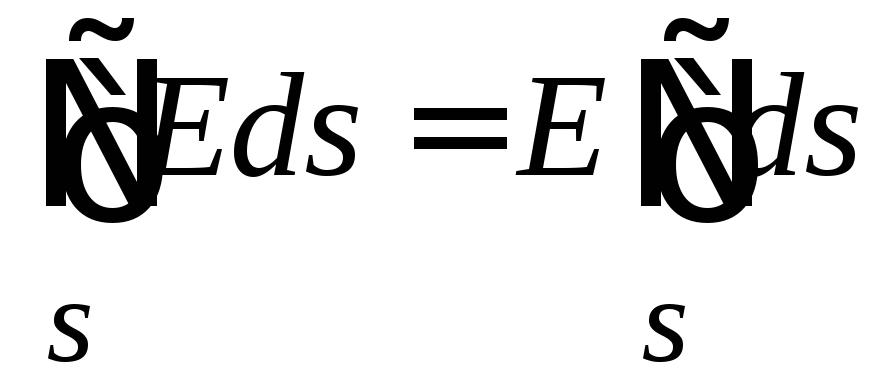

.

Интеграл на елементарните повърхности итепо цялата повърхност е равна на площта на тази повърхност ите, В този случай повърхността е сфера, чиято област ите   = 4 ° r 2 .

Така потокът на вектора на интензитета през затворена повърхност в този случай е равен на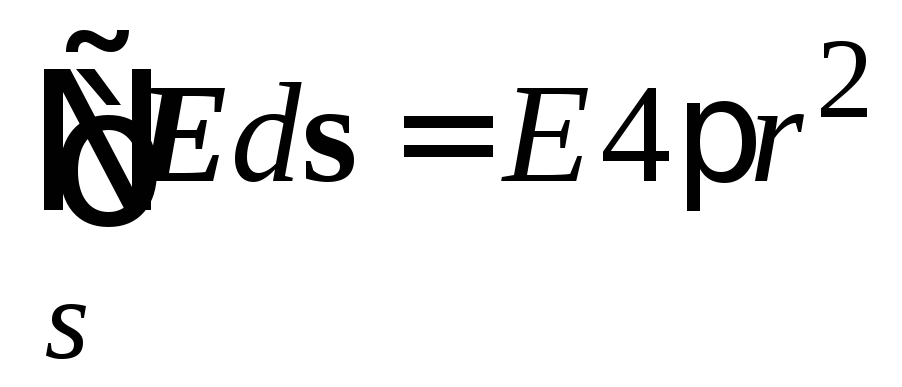

.

Подменяйки израза, за да изчислим интензитета, получаваме

.

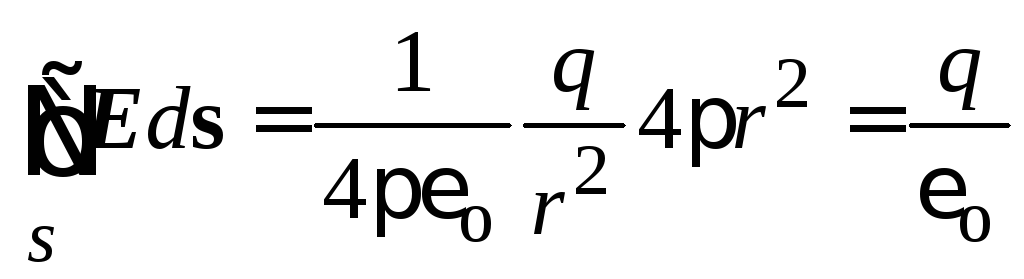Може да се покаже, че потокът на вектора на силата на полето на точков заряд през затворена повърхност ще бъде равен на 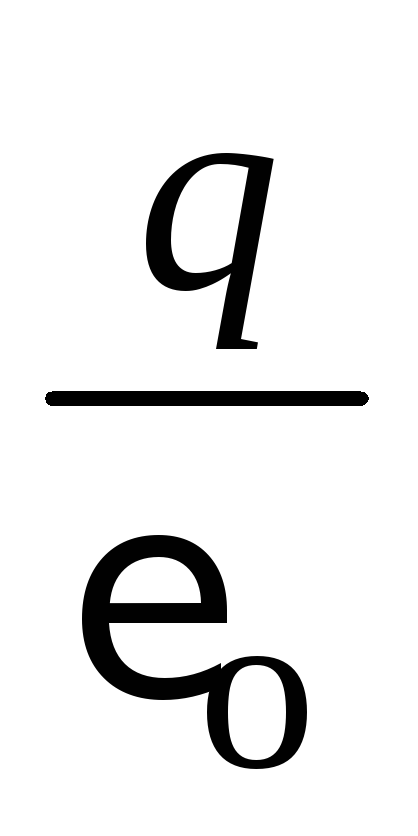и в случая, когато зарядът не е в центъра на сферичната повърхност.

Освен това, потокът ще бъде същият, дори ако повърхността има някаква форма.

Ако повърхността покрива няколко заряда р аз   , потокът на всеки от зарядите през затворена повърхност ще бъде равен на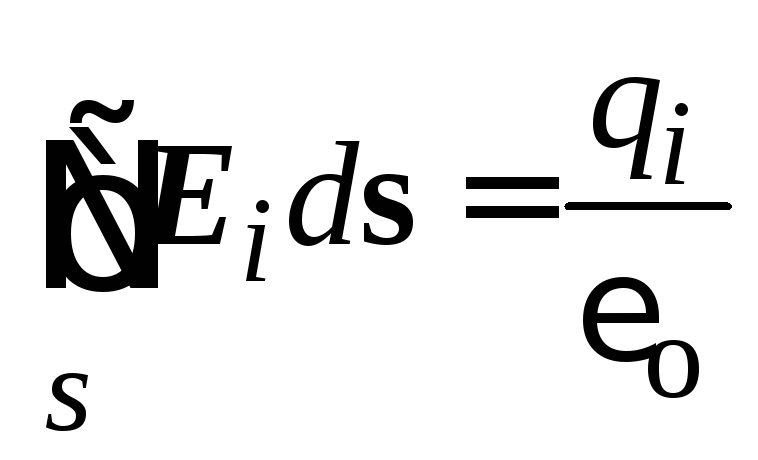

, Общият поток, създаден от всички такси, ще бъде равен на

.

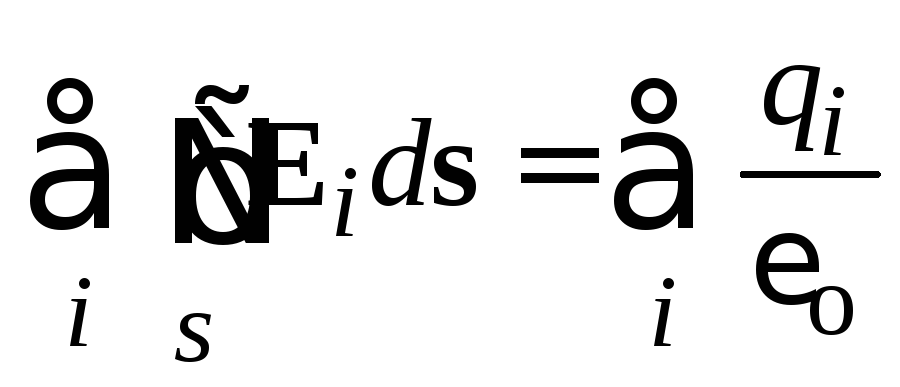Промяна на последователността на сумиране и интегриране и отчитане на това в съответствие с принципа на суперпозиция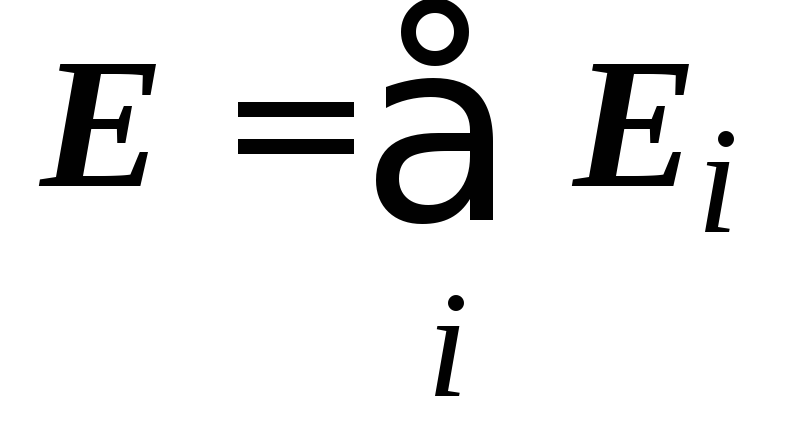

, да се

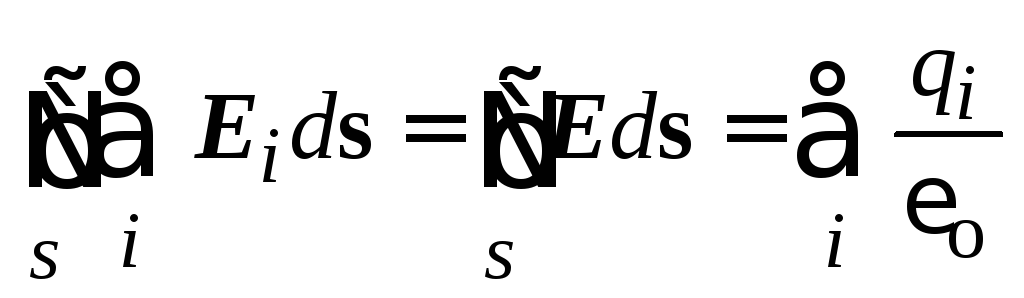където E   - вектор на силата на полето, създаден от всички заряди, покрити от затворена повърхност.

Така анализът ни позволи да получим следната връзка:

.

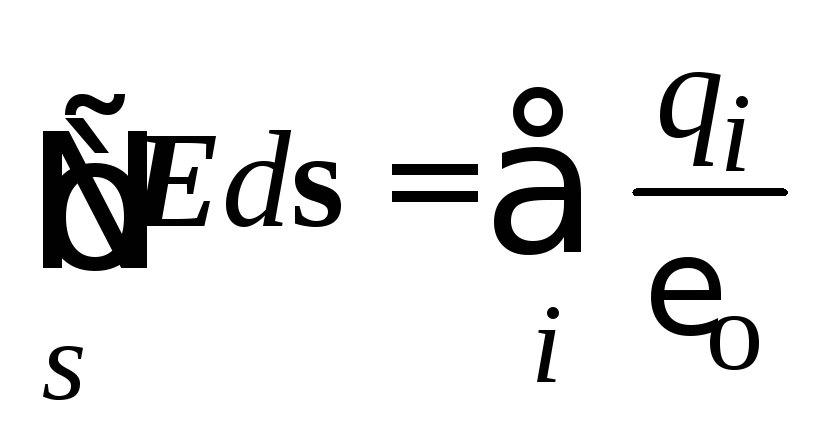Тази връзка има универсален характер и се нарича теорема на Гаус: потокът на вектора на силата на електрическото поле през затворена повърхност е равен на отношението на сумата на зарядите, покрити от тази повърхност към електрическата константа.

Забележка: в израза на теоремата на Гаус няма характеристики на позицията на зарядите р аз .

Това означава, че потока на вектора на интензитета не зависи от това как се намират зарядите, покрити от затворена повърхност. Освен това, потока на вектора на интензивността няма да се промени, ако взаимното подреждане на зарядите, покрити от повърхността, се промени.

Практическото значение на теоремата на Гаус е, че с негова помощ е значително опростено изчисляването на полета, създадени от симетрични разпределения на заряда. В този случай можете да изберете такава повърхност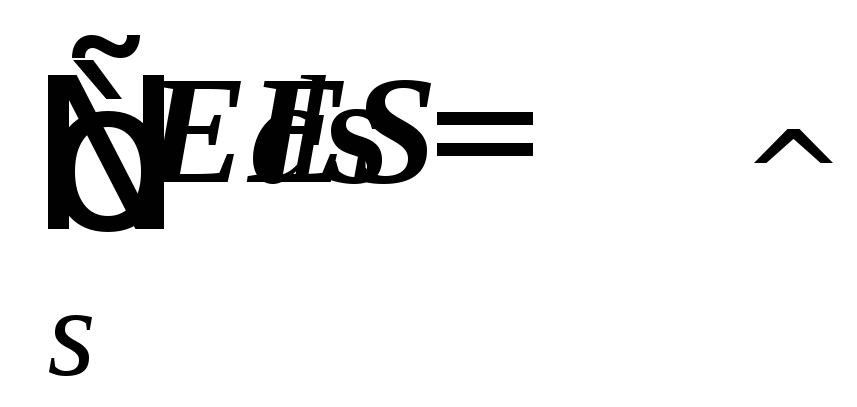

където S    е площта на частта от затворената повърхност, проникната от електрическото поле.

E r = Ф S = 4 2 = 2 B m.

Пример 2: платформата S = 3m2 е в еднородно поле от 100 N / Cl. Колко линии пресичат тази област, ако ъгълът е 30º (фиг. 2.4).

E E = E sin 300 = 50 N / C

F = E = · S = 50 · 3 = 150 линии

2.2. Напрежението на векторния поток.

И така, чрез примери показахме, че ако силовите линии са хомогенни

напрежението на електрическото поле E прониква в определена област, тогава напрежението на напрежението (използвано за извикване на броя на силовите линии през зоната) ще бъде определено по формулата

Фр E = ES = EScos α = En S,

където En е произведението на вектораE от нормана към това място (фиг. 2.5).

А стойността на Ф Е тук се нарича потока на вектора на интензитета на електрическото поле през областта S, т.е. определение:

Общият брой на силовите линии, преминаващи през повърхността S, се нарича вектор на потока на PU елементи през тази повърхност.

В векторна форма можете да пишете

		Ф Е = (Е, S) - скаларен продукт на два вектора,
	където векторът е S = n S.
	Т.е. векторния поток
			Е е скалар, който, в зависимост от ъгъла а

могат да бъдат както положителни, така и отрицателни , Разгледайте (Фиг. 2.6, 2.7).

За тази конфигурация потокът през повърхността А е отрицателен (пребройте броя на силовите линии).

Фиг. 2.6. 2.7

За фигура 2.6 - повърхността А 1 обгражда положителния заряд и тук потокът е насочен навън, т.е. F Е\u003e 0. Повърхност А 2 - обгражда отрицателния заряд и тук Ф Е< 0 направлен внутрь.

За Фигура 2.7 потокът ще бъде ненулев, ако общият заряд в повърхността е ненулев. Т.е. Потокът зависи от заряда. Това е значението на теоремата на Гаус.

2.3. Теорема Остроградски-Гаус.

Така че нека си припомним, че потока на вектора на електрическото поле е равен на броя на линиите на интензитета, преминаващи през областта S (фиг. 2.8).

dFE = EdScos a = En dS

R 2)

q 4 πR 2 = q

4 πε 0 R 2 2 2 ε 0

Т.е. в еднородно поле = Е = ЕS в произволно електрическо поле

	ФЕ = ∫ Еn dS = ∫ E dS
	d S r = dS n r - във векторна форма
	Ориентацията на dS в пространството се определя с помощта на единичния вектор n r. Т.е.
	- посоката съвпада с посоката на външната норма към повърхността.
	Изчислете потока на вектор Е през	затворена повърхност	S около

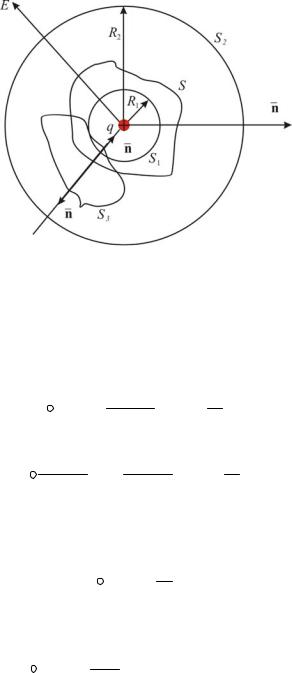
точков заряд q (фиг. 2.9.).

Центърът на кръга съвпада с центъра на заряда. Радиусът на сферата S1 е R1. Най-

всяка точка на повърхността S 1 проекцията E на посоката на нормалната норма е еднаква и е равна на

E n =
	4 πε
След това преминавайте през S 1
ФЕ = d En dS =				2 4 πR 1 2 =
	4 πε0 R1

Изчислява се потокът през S 2 (радиус

FE = π 4 πε q R 2 dS =

S 2 r 0 2

Линиите на напрежение E започват и завършват в безкрайност) от непрекъснатостта на линията, от което следва, че потокът на произволна повърхност S ще бъде равен на една и съща стойност:

ФЕ = ∫ Еn dS =

Полученият резултат е валиден не само за едно зареждане, но и за произволно разположени заряди в повърхността.

	ФЕ = ∫ Еn dS =	Σq	- Теорема на Гаус

Потокът на вектора на електрическото поле през затворена повърхност във вакуум е равен на алгебричната сума на всички заряди, разположени вътре в повърхността, разделена на ε0.

При изчисляване на потока през затворена повърхност, нормалният вектор n

ограничена от дадена повърхност, се създава положителен поток, линиите, влизащи в обема, са отрицателен поток.

Ако поставим друга S 3 повърхност между нашите сфери, не го правете

покриване на заряда, тогава, както може да се види от (фиг. 2.9). Всяка линия на напрежение Е ще пресече тази повърхност два пъти: веднъж на положителната страна ще влезе

в повърхността S3, друг път - от отрицателната страна - ще излезе от повърхността S3.

Най- резултатът е алгебрична сума от линии на напрежение, преминаващи през тях

затворената повърхност на S3 ще бъде равна на нула, т.е. общият поток, преминаващ през S3, е нула.

По този начин за точково зареждане q, общият поток през всяка затворена повърхност S ще бъде равен на:

FE = 0 - ако зарядът е разположен извън затворена повърхност и този резултат

не зависи от формата на повърхността и знакът за потока съвпада със знака на заряда.

В общия случай електрическите заряди могат да бъдат „размазани” с определена насипна плътност ρ, различна в различните места на пространството. Спомнете си друга концепция - плътността на насипния заряд

ρ =

където dV е безкрайно малък обем.

Чрез физически безкрайно малък обем dV трябва да разберем такъв обем, който, от една страна, е достатъчно малък, че в неговата плътност на заряда се счита равен, а от друга, достатъчно голям, така че дискретността на заряда да не може да се появи, т.е. че всяка такса е кратна на цяло число на елементарни такси или P + (протон). Тогава общата такса

I qi = ∫ ρdV
Тогава от теоремата на Гаус (2.3.7.) Пишем
	ε 0V ∫

Това е друга форма на писане на теоремата на Гаус, ако зарядът е непрекъснат.

Необходимо е да се обърне внимание на следното обстоятелство: докато r

самото поле Е зависи от конфигурацията на всички заряди, потока Е през произволна затворена повърхност се определя само от алгебричната сума на зарядите вътре в повърхносттаS. Това означава, че ако движите зарядите, тогава Е ще се променя навсякъде и на повърхността S, но потокът на вектора Е през тази повърхност ще остане същият. Удивителното свойство на вектора на напрежението е Е.

2.4. Диференциална форма на теоремата на Гаус.

Най- установява връзка между плътността на обемния зарядρ и changeE в квартала на дадена точка в пространството