Käännymme nyt pallomaiseen (piste) varaukseen. Yllä on osoitettu, että pallon yli tasaisesti jakautuneen varauksen luoma sähkökenttä Q, ei riipu pallon sädestä. Kuvittele se tietyltä etäisyydeltä
r pallon testistä on testilataus q. Kenttävoimakkuus kohdassa, jossa varaus on, 
Kuvio näyttää graafin pistevarausten välisen sähköstaattisen vuorovaikutuksen voimakkuuden riippuvuudesta niiden välisestä etäisyydestä. Sähkökentän työn löytäminen testilataa siirrettäessä q kaukaa r etäisyyteen Rmurtaa tämä aukko pisteiksi r 1 , r 2 ,..., r n tasa-arvoisiin segmentteihin. Keskimääräinen varaukseen vaikuttava voima q segmentin sisällä [ rr 1] on yhtä suuri 
Tämän joukon työ tällä sivustolla:
Samanlaiset lausekkeet työstä saadaan kaikille muille osioille. Siksi koko työ:
Identtiset termit, joissa on vastakkaiset merkit, tuhotaan, ja lopulta saamme:
- kenttätyöt maksutta 
- potentiaaliero 
Nyt tavoitteemme on löytää kenttäpisteen potentiaali äärettömyyteen nähden R äärettömyyteen ja lopulta saada:
Joten pistevarauksen kentän potentiaali on käänteisesti verrannollinen etäisyyteen varaukseen.
24. Mahdollinen varausenergia varausjärjestelmän kentällä. Potentiaalien superpositioperiaate. Potentiaalien superpositioperiaate
Mikä tahansa mielivaltaisen monimutkainen sähköstaattinen kenttä voidaan esittää pistevarausten kenttien superpositiona. Jokaisella tällaisella kentällä valitussa pisteessä on tietty potentiaali. Koska potentiaali on skalaarimäärä, kaikkien pistevarausten kentän tuloksena syntyvä potentiaali on yksittäisten varausten kenttien potentiaalien 1, 2, 3, ... algebrallinen summa: \u003d 1 + 2 + 3 + ... Tämä suhde on suora seuraus sähkökenttien superpositioperiaatteesta.
Mahdollinen varausenergia sähkökentässä. Jatkamme kehojen painovoimaisen vuorovaikutuksen ja varausten sähköstaattisen vuorovaikutuksen vertailua. Kehon massa mmaapallon gravitaatiokentällä on potentiaalista energiaa. Painovoima on yhtä suuri kuin potentiaalienergian muutos, joka otetaan vastakkaisella merkillä:
A \u003d -(W p2 - W p1) = mGH.
(Jäljempänä tarkoitamme energiaa kirjeellä W.) Aivan kuin kehon massa m painovoimakentässä on potentiaalienergiaa suhteessa kehon massaan, sähköstaattisessa kentässä olevalla sähkövarauksella on potentiaalienergiaa W p verrannollinen lataukseen q. Sähköstaattisen kentän voimien toiminta yhtä suuri kuin sähkökentän varauksen potentiaalisen energian muutos, otettuna vastakkaisella merkillä:
A \u003d -(W p2 - W p1) . (40.1)
25. Mahdolliset erot. Potentiaalipotentiaaliset pinnat
Potentiaalinen potentiaalinen pinta - pinta, jonka jokaisella pisteellä on sama potentiaali.
Kuten työn ja potentiaalien suhteesta seuraa:
varauksen siirron aikana potentiaalisesti potentiaalisia pintoja pitkin, sähkökenttä ei toimi, koska.
Toiminta nollasta poikkeavalla voimalla on yhtä suuri kuin nolla vain, jos voimavektori on kohtisuorassa siirtovektoriin nähden. Tästä seuraa, että jännitysviivat ovat kohtisuorassa potentiaalisten potentiaalisten pintojen kanssa. Esimerkkejä potentiaalipotentiaalisista pinnoista ovat pallopisteet pistevarauksen kentälle ja rinnakkaiset tasot homogeenisille kentille (kuva 3).
Potentiaalierot (jännite)kahden pisteen välillä on yhtä suuri kuin kentän suhde siirrettäessä lataus aloituspisteestä loppuun tämän latauksen moduuliin: U \u003d φ 1 - φ 2 \u003d -Δφ \u003d A / q, A \u003d - (W п2 - W п1) \u003d -q (φ 2 - φ 1) \u003d -qΔφ
Potentiaaliero mitataan volteissa (V \u003d J / C) .Suhde sähköstaattisen kentän voimakkuuden ja potentiaalierojen välillä: E x = Δφ / Δ x Sähköstaattisen kentän voimakkuus on suunnattu laskevaan potentiaaliin. Mitattu volteissa jaettuna metreillä (V / m)
sähköstaattisella kentänvoimalla
Kuten yhtälöstä (1.11) voidaan nähdä, varauksen potentiaalienergia qvastaava kenttä Q riippuu maksun määrästä q. Toistamalla saman päättelyn kuin kaavan (1.3) johdannossa sähkökentän voimakkuudelle, päätellään, että varauksen potentiaalisen energian suhde kentän tietyssä pisteessä varauksen suuruuteen ei riipu tämän latauksen suuruudesta ja voi siten toimia yhtenä toisena ominaisuutena kenttään. Tätä ominaisuutta kutsutaan potentiaaliksi.
Potentiaalin mittayksikkö - Voltti: 
. Koska äärettömyydessä vuorovaikuttavien varausten potentiaalienergia on nolla, niin kentän potentiaali äärettömyydessä on myös nolla. Lausekkeesta (1.12) se seuraa potentiaalin määritelmä on kentän tiettyyn pisteeseen sijoitetun yksittäisen positiivisen varauksen potentiaalienergia.
Siten potentiaali on kentän energiaominaisuus. Kaavojen (1.11) ja (1.12) vertailusta seuraa, että pistevarauksen luoma potentiaali tietyssä kentän pisteessä määritellään
Kaavoista (1.6), (1.9) ja (1.12) seuraa:
tai pistevarauksen siirtäminen kahden pisteen välillä sähköstaattisessa kentässä on yhtä suuri kuin varauksen arvon tulo lähtö- ja loppupisteiden potentiaalierolla:
. (1.14)
Koska työ voidaan tallentaa myös sähkökentän voimakkuuden avulla
, (1.15)
sitten kaavojen (1.14) ja (1.15) vertailusta saadaan
. (1.16)
Sekä jännitys että potentiaali ovat saman sähköstaattisen kentän kaksi ominaisuutta tietyssä pisteessä. Siksi niiden välillä on oltava jonkin verran kirjeenvaihtoa, yhteyttä. Tämän suhteen luomiseksi otamme huomioon panoksen siirtämisen akselia pitkin x etäisyydellä dx, kun taas potentiaaliero pienenee dj:
.
Viimeisimmästä löytämästämme suhteesta (vähentämällä q)
Osittaisen johdannaisen symboli ¶ johdetaan kaavaan (1.17) korostamaan, että siirtymä otetaan huomioon vain akselia pitkin x. Samoin löydämme muita sähkökentän komponentteja ja. Löytyneistä vektorin komponenteista voit tehdä koko vektorin:
. (1.18)
täällä i, j, k
- yksikkövektorit akselien suunnassa x, y, z. Lauseke (1.18) voidaan kirjoittaa lyhennetyssä muodossa käyttämällä Ñ-operaattoria - luetaan ”nabla”: 
. Koska tämän operaattorin soveltamisen seurauksena skalaarifunktioon saamme tämän funktion gradienttivektorin
Or. (1,19)
Kuvailla potentiaalin jakautumista käytä käsitettä ekvipotentiaalinen pinta on pinta, jonka kaikilla pisteillä on sama potentiaali . Koska pistevarauksen kentän potentiaali riippuu vain etäisyydestä varaukseen (katso kaava (1.13)), tästä seuraa, että samankeskiset pallot ovat potentiaalipotentiaalisia pistevarauksessa. Toisaalta sähkökentän viivat on suunnattu sädettä pitkin positiivisesta varauksesta negatiiviseen varaukseen. Siksi pistevarauksen tapauksessa jännitysviivat ovat kohtisuorassa potentiaalipotentiaalien kanssa. Voidaan kuitenkin osoittaa, että tämä päätelmä on yleinen - jännitysviivat ovat aina kohtisuorassa potentiaalisten potentiaalisten pintojen kanssa.
1.5 Gauss-lause sähköstaattisen kentän voimakkuudeksi integraali- ja differentiaalimuodoissa
Päällekkäisyysperiaate (1.5) antaa meille periaatteessa mahdollisuuden laskea minkä tahansa maksujärjestelmän kenttä. Jonkin tyyppisissä symmetriaongelmissa jännityksen laskentaa kuitenkin yksinkertaistetaan huomattavasti Gauss-lauseen avulla. Ennen kuin lausumme tämän lauseen, esittelemme käsitteen jännitysvektorin perusvirtauksesta mielivaltaisen alueen läpi. Jännitysvektorin virtaus mielivaltaisen perusalustan dS läpi on tämän vektorin skalaarituote pintaelementin avulla .
15 §. VIRRASysteemin sähköiset maksut. TYÖ ALKUPERÄISEN MOBIILINEN LATAAMINEN
Peruskaavat
Sähkökentän potentiaali on arvo, joka on yhtä suuri kuin kentän tiettyyn pisteeseen sijoitetun pistepositiivisen varauksen potentiaalienergian suhde tähän varaukseen;
\u003d P / Q,
tai sähkökentän potentiaali on arvo, joka on yhtä suuri kuin kenttävoimien työsuhde, joka siirtää pistepositiivisen varauksen kentän tietystä pisteestä äärettömyyteen tähän varaukseen:
=/ Q.
Sähkökentän potentiaali äärettömyyteen on ehdollisesti yhtä suuri kuin nolla.
Huomaa, että kun varaus liikkuu sähkökentässä, työ vS ulkoiset voimat ovat yhtä suuret kuin työ sP kentän voimakkuus ja vastapäätä merkissä:
vS = – sP .
Pistevarauksen luoma sähkökentän potentiaali Qetäisyydessä rmaksusta
Latausta kantavan metallin luoman sähkökentän potentiaali Qpallo säde R, etäisyydellä pallon goottikeskipisteestä:
pallon sisällä ( r<R)
;
pallon pinnalla ( r=R)
;
ulkopuolella (r>
R)
.
Kaikissa kaavoissa, jotka annetaan varautuneen pallon potentiaalille, on pallon ympäröivän homogeenisen äärettömän dielektrisen dielektrisyysvakio.
Järjestelmän luoman sähkökentän potentiaali npistevarauksia, tietyssä pisteessä sähkökenttien superpositioperiaatteen mukaisesti on yhtä suuri kuin algebralliset summapotentiaalit 1 , 2 , ... , n luotu yksittäisistä pistemaksuista Q 1 ,Q 2 , ...,Q n :
Energia Wpistevarausjärjestelmän vuorovaikutukset Q 1 ,Q 2 , ...,Q n määritetään työllä, jonka tämä varausjärjestelmä voi suorittaa, kun ne poistetaan suhteessa toisiinsa äärettömyyteen, ja se ilmaistaan \u200b\u200bkaavalla
,
missä minä - kaikkien luoman kentän potentiaali n-1 lataus (paitsi ensimmäinen) paikassa, jossa lataus sijaitsee Q minä .
Potentiaali liittyy suhteessa sähkökentän voimakkuuteen
E\u003d –Grad.
Pallomaisella symmetrialla varustetun sähkökentän tapauksessa tämä suhde ilmaistaan \u200b\u200bkaavalla
,
tai skalaarisessa muodossa
,
ja homogeenisen kentän tapauksessa, ts. kentän, jonka intensiteetti sen jokaisessa pisteessä on sama sekä absoluuttisessa arvossa että suunnassa,
E=( 1 – 2 ,)/d,
missä 1 i 2 - kahden potentiaalisen pinnan pisteiden potentiaalit; d - näiden pintojen välinen etäisyys sähköjohtoa pitkin.
Sähkökentän tekemä työ pistevarausta siirrettäessä Qyhdestä kentän pisteestä potentiaalisella 1 toiselle, jolla on potentiaalia 2 ,
=Q( 1
- 2
) tai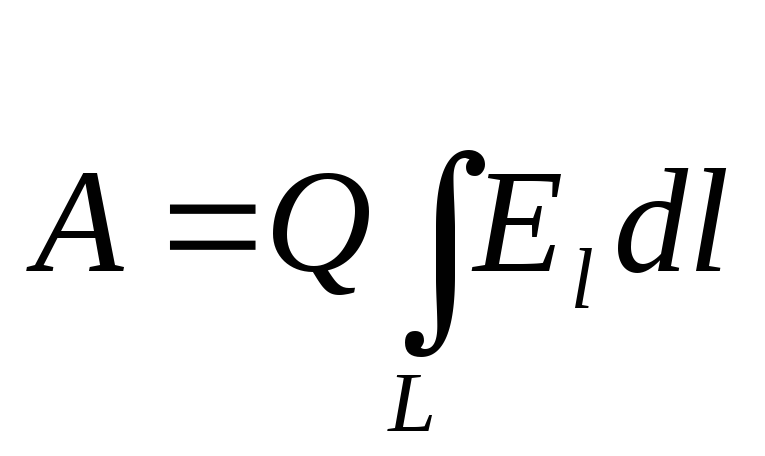 
,
jossa E l - jännitysvektoriprojektio Eliikesuuntaan; dl - liikettä.
Homogeenisen kentän tapauksessa viimeinen kaava on muoto
= QElcos ,
jossa l- siirtymä; - kulma vektorisuuntien välillä Eja liikkuvat l.
Esimerkkejä ongelmien ratkaisemisesta
Esimerkki 1Positiiviset lataukset Q 1 \u003d 3 μC ja Q 2 \u003d 20 nC ovat tyhjössä etäältä r 1 \u003d l, 5 m toisistaan. Määritä työ , joka on tehtävä, jotta lataukset saadaan lähemmäksi etäisyyttä r 2 \u003d 1 m.
Päätös.Laita ensimmäinen lataus Q 1 pysyy paikallaan ja toinen Q 2 ulkoisten voimien vaikutuksesta se liikkuu varauksen luomassa kentässä Q 1 lähestyi häntä etäältä r 1 \u003d t, 5 m - r 2 \u003d 1 m .
työ A "ulkoinen voima latauksen siirtämiseksi Qyhdestä kentän pisteestä potentiaalisella 1 toiselle, jonka potentiaalinen потенциал 2 on yhtä suuri ja vastakkaisella merkillä toimimiseen kenttävoimat latauksen siirtämiseksi samojen pisteiden välillä:
A "\u003d -A.
työ kenttäjoukot vastuussa liikkeestä =Q( 1 - 2 ). Sitten työskentele A "ulkoiset voimat voidaan kirjoittaa
" = –Q( 1 - 2 )=Q( 2 - 1 ). (1)
Polun aloitus- ja lopetuspisteiden potentiaalit ilmaistaan \u200b\u200bkaavoilla
;
.
Lausekkeiden korvaaminen 1 i 2 kaavassa (1) ja ottaen huomioon, että tässä tapauksessa siirretty maksu Q=Q 2 saamme
. (2)
Koska 1 / (4 0 )=910 9 m / f, sitten korvaamalla kaavan (2) määrien arvot ja laskemalla, löydämme
"\u003d 180 mJ.
Esimerkki 2Löydä työ veloittaa siirtokentät Q\u003d 10 nC pisteestä 1 kohtaan 2 (Kuva 15.1), joka sijaitsee kahden vastakkaisella varauksella pintatiheyden ollessa \u003d 0,4 μC / m 2 ääretön yhdensuuntainen taso, etäisyys ljonka välissä on 3 cm.
P 
osoitusta.On olemassa kaksi tapaa ratkaista ongelma.
1. menetelmä.Kenttätyö pakottaa siirtämään varauksen Q pisteestä 1 kentät, joilla on potentiaalinen 1 kohtaan 2 kentät, joilla on potentiaalinen 2 löydämme kaavan mukaan
=Q( 1 - 2 ). (1)
Mahdollisuuksien määrittäminen pisteissä 1 ja 2 piirrä potentiaalipotentiaalit I ja II näiden pisteiden läpi. Nämä pinnat ovat tasoja, koska kahden tasaisesti varautuneen ääretön yhdensuuntaisen tason välinen kenttä on tasainen. Sellaisen kentän suhteen
1 - 2 =el, (2)
jossa E -kentän voimakkuus; l - etäisyys potentiaalisten potentiaalisten pintojen välillä.
Kenttävoimakkuus rinnakkaisten loputtomasti vastakkaisesti latautuneiden tasojen välillä E=/ 0 . Korvataan tämä lauseke Ekaavaan (2) ja sitten lauseke 1 - 2 kaavassa (1) saadaan
= Q( / 0 ) l.
2. menetelmä.Koska kenttä on homogeeninen, varaukseen vaikuttava voima Q, kun se on vakiona. Siksi työ siirtää latauksen pisteestä 1 kohtaan 2 voidaan laskea kaavalla
\u003d F rcos, (3)
jossa F - panoksella vaikuttava voima; r- maksunsiirtomoduuli Qpisteestä 1 kohtaan 2; - kulma liikesuuntien ja voiman välillä . mutta F= QE= Q( / 0 ). Korvataan tämä lauseke Ftasa-arvoon (3) ja huomauttaen myös, että rcos \u003d lsaamme
=Q(/ 0 )l. (4)
Siten molemmat ratkaisut johtavat samaan tulokseen.
Korvataan lausekkeessa (4) määrien arvo Q, , 0 ja llöydämme
\u003d 13,6 μJ.
Esimerkki 3Ohuella langalla, joka on taivutettu säteen ympyrän kaaria pitkin R,
varaus, jonka lineaarinen tiheys \u003d 10 nC / m, jakautuu tasaisesti. Tunnista jännite Eja tällaisen p: n luoman sähkökentän potentiaali 
hajautettu maksu yhdessä pisteessä oisamaan aikaan kaaren kaarevuuskeskipisteen kanssa. pituus llanka on 1/3 kehästä ja on yhtä suuri kuin 15 cm.
Päätös.Valitsemme koordinaattiakselit siten, että lähtö vastaa kaarun kaarevuuskeskusta ja akselia atsijaitsi symmetrisesti kaaren päihin nähden (kuva 15.2). Valitse langasta elementti, jonka pituus on d l. Lataa d Q\u003d d lValitulla alueella sijaitsevia voidaan pitää pisteinä.
Määritämme sähkökentän voimakkuuden pisteessä oi. Tätä varten löydämme ensin jännitteen d Elatauksen luoma kenttä d Q:
,
jossa relementistä d suunnattu -radiusvektori lsiihen pisteeseen, jossa jännitys lasketaan. Ilmaise vektori d Eprojektioiden kautta dE x cja dE y koordinaattiakselilla:
,
jossa minäja j- yksikkösuuntavektorit (yksikkövektorit).
jännitys Elöytää integroinnin perusteella:
.
Integrointi suoritetaan pituuskaaria pitkin l. Symmetrian nojalla integraali 
yhtä suuri kuin nolla. sitten
, (1)
jossa 
. koska r=R\u003d const ja d l=Rd.
Korvaa löydetty lauseke dE y kohdassa (1) ja ottaen huomioon kaaren symmetrinen järjestely akseliin nähden Voi,otamme integraatiorajat 0: sta / 3: seen ja kaksinkertaistamme tuloksen;
.
Korvaa määritellyt rajat ja ilmaisee Rläpi kaaren pituuden (3 l= 2 r), saamme
.
Tämä kaava osoittaa, että vektori Evastaa akselin positiivista suuntaa OuKorvaa arvo lviimeiseen kaavaan ja laskelmien tekemisen jälkeen löydämme
E\u003d 2,18 kV / m.
Määritämme sähkökentän potentiaalit pisteessä oi. Ensin löydämme pistevarauksen d luoma potentiaalinen d Qpisteessä Tietoja:
korvata rpäälle Rja integroida:
Koska l=2
R/3,
\u003d / (6 0 ).
Suoritettuaan laskelmat tätä kaavaa käyttämällä saadaan
esimerkki4 . Sähkökentän luo pitkä sädesylinteri R= 1cm , tasaisesti varautunut lineaarisella tiheydellä \u003d 20 nC / m. Määritä kentän kahden etäisyyksillä sijaitsevan pisteen potentiaaliero 1 \u003d 0,5 cm ja ja 2 \u003d 2 cm sylinterin pinnasta sen keskiosassa.
Päätös.Potentiaalieron määrittämiseksi käytämme kenttävoimakkuuden ja potentiaalimuutoksen välistä suhdetta E\u003d -luokka. Kenttälle, jolla on aksiaalinen symmetria, joka on sylinterin kenttä, tämä suhde voidaan kirjoittaa muodossa
E \u003d - (d / d r) tai d \u003d - Ed r.
Integroimalla viimeisen lausekkeen löydämme kahden pisteen potentiaaliero välimatkan päässä r 1 ja r 2 sylinterin akselilta;
. (1)
Koska sylinteri on pitkä ja pisteet otetaan lähellä sen keskiosaa, kentänvoimakkuuden ilmaisemiseksi voit käyttää kaavaa 
. Korvataan tämä lauseke Etasa-arvoon (1), saamme
(2)
Koska määrät r 2 ja r 1 kirjoita kaava suhteen muodossa, ne voidaan ilmaista millä tahansa, mutta vain samoilla yksiköillä:
r 1 \u003d R + a 1 = 1,5 cm; r 2 =R+ 2 \u003d 3cm .
Korvataan suuruuden , arvot 0 ,r 1 ja r 2 kaavaan (2) ja laskemaan, löydämme
1 - 2 \u003d 250 V.
Esimerkki 5Sähkökentän muodostaa ohut sauva, jolla on tasaisesti jakautunut varaus pituudella \u003d 0,1 μC / m. Määritä kentän potentiaali sauvan päistä etäällä olevassa pisteessä etäisyydellä, joka vastaa sauvan pituutta.
Päätös.Tankoon sijoitettua varausta ei voida pitää pisteenä, joten käytä suoraan kaavaa potentiaalin laskemiseksi
, (1)
voimassa vain pistemaksuihin, se on mahdoton. Mutta jos murskaamme sauvan elementtisegmentteihin d l, sitten latausd lJokaisessa niistä sijaitsevaa voidaan pitää pisteenä ja sitten kaava (1) on kelvollinen. Soveltamalla tätä kaavaa saamme
, (2)
jossa r - sen pisteen etäisyys, jossa potentiaali määritetään tankoelementtiin.
Kuv. 15.3 seuraa, että d l=(rd / cos). Tämän ilmaisun korvaaminen d lkaavassa (2) löydämme 
.
Integroidaan saatu lauseke alueelle 1
da 2
, saamme potentiaalin, jonka koko tankoon jakautunut varaus luo: 
.
pisteen symmetria suhteessa sauvan päihin, meillä on 2
= 1
ja siksi 
.
siksi,
Koska 
(katso välilehti 2), sitten 
.
Korvaamalla integraation rajat, saamme
Kun olemme tehneet laskelmia tämän kaavan avulla, löydämme
Esimerkki 6Elektroni, jonka nopeus on v \u003d 1.8310 6 m / s, lensi tasaiseen sähkökenttään kentänvoimakkuusvektoria vastakkaiseen suuntaan. Mikä on potentiaalinen ero? Uelektronin on läpäistävä, jotta hänellä olisi energiaa E minä \u003d 13,6 eV *? (Hallussaan tällaista energiaa, elektroni törmäyksessä vetyatomin kanssa voi ionisoida sen. 13,6 eV: n energiaa kutsutaan vedyn ionisaatioenergiaksi.)
Päätös.Elektronin on läpäistävä tällainen potentiaaliero U,niin että tässä hankittu energia Wyhteensä kineettisen energian kanssa T, jonka elektronilla oli ennen kentälle tuloa, vastasi ionisaatioenergiaa vastaavaa energiaa E minä ,
t. e. W+
T=
E minä .
Ilmaistaan \u200b\u200btässä kaavassa W=
euja T=(mv 2
/ 2), saamme eu+(mv 2
/2)=E minä . Täältä 
.
___________________
* Elektroni voltti (eV) on energia, jonka hiukkanen saa, kun sen varaus on yhtä suuri kuin elektronin varaus, potentiaaliero yli 1 V. Tämä ei-systeeminen energiayksikkö on tällä hetkellä hyväksytty käytettäväksi fysiikassa.
Lasketaan SI-yksiköinä:
U \u003d 4,15V.
Esimerkki 7Määritä alkuperäinen nopeus υ 0 protonien läheisyys, jotka sijaitsevat riittävän suurella etäisyydellä toisistaan, jos minimietäisyys r min, jolla ne voivat tulla lähelle, on 10 - 11 cm.
Kahden protonin välillä toimivat repeävät voimat, joiden seurauksena protonin liike hidastuu. Siksi ongelma voidaan ratkaista sekä inertiakoordinaattijärjestelmässä (joka liittyy kahden protonin massakeskipisteeseen) että ei-inertiaalisessa (joka liittyy yhteen nopeasti liikkuvista protoneista). Toisessa tapauksessa Newtonin lakeja ei sovelleta. D'Alembert-periaatteen soveltaminen on vaikeaa, koska järjestelmän kiihtyvyys muuttuu. Siksi on tarkoituksenmukaista tarkastella ongelmaa inertiaviitekehyksessä.
Asetamme alkuperä kahden protonin massakeskipisteeseen. Koska kyse on samoista hiukkasista, massan keskipiste on kohdassa, joka puolittaa hiukkasia yhdistävän segmentin. Massakeskuksen suhteen hiukkasilla on samanaikaisesti sama nopeuskerroin. Kun hiukkaset ovat riittävän suurella etäisyydellä toisistaan, nopeus υ 1 jokainen hiukkanen on puoli υ 0 , t. e. υ 1 =υ 0 /2.
Ongelman ratkaisemiseksi käytämme energiansäästölakia, jonka mukaan mekaaninen kokonaisenergia Eeristetty järjestelmä on vakio, ts.
E \u003d T +P ,
jossa T- molempien protonien kineettisten energioiden summa suhteessa massakeskipisteeseen; P on varausjärjestelmän potentiaalinen energia.
Ilmaise potentiaalienergia liikkeen P 1 ja viimeisissä P 2 -momenteissa.
Alkuvaiheessa protonit olivat ongelman tilan mukaan suuren etäisyyden päässä, joten potentiaalienergia voidaan jättää huomiotta (P 1 \u003d 0). Siksi ensimmäisellä hetkellä kokonaisenergia on yhtä suuri kuin kineettinen energia T 1 protonit, ts.
E \u003d T l . (1)
Viimeisellä hetkellä, kun protonit saapuvat mahdollisimman lähelle, nopeus ja kineettinen energia ovat yhtä suuret kuin nolla, ja kokonaisenergia on yhtä suuri kuin potentiaalienergia P2, ts.
E \u003dP 2 . (2)
Yhtälöillään yhtälöiden (1) ja (2) oikea puoli, saadaan
T1 \u003d P2. (3)
Kineettinen energia on yhtä suuri kuin protonien kineettisten energioiden summa:
(4)
Kahden varauksen järjestelmän potentiaalinen energia Q 1 ja Q 2, joka sijaitsee tyhjiössä, määritetään kaavalla 
jossa r- maksujen välinen etäisyys. Tämän kaavan avulla saamme
(5)
Kun otetaan huomioon yhtäläisyydet (4) ja (5), kaava (3) on muoto
mistä alkaen 
Suoritettuaan laskelmat saadun kaavan mukaan, löydämme υ 0 =2,35 Mm / s
Esimerkki 8Elektroni, jolla ei ole alkuperäistä nopeutta, on ylittänyt potentiaaliero U 0 =10
kV ja lensi potentiaalieroon ladatun tasaisen kondensaattorin levyjen väliseen tilaan U l \u003d 100 V, viiva ABlevyjen suuntaisesti (kuva 15.4). etäisyys dlevyjen välissä on 2 cm l 1 kondensaattorilevy elektronin lennon suunnassa, joka on yhtä suuri kuin 20 cm. Määritä etäisyys aurinkonäytöllä P,kaukana kondensaattorista l 2 \u003d 1 m.
PÄÄTÖS: Elektronin liike kondensaattorin sisällä koostuu kahdesta liikkeestä: 1) inertin avulla linjaa pitkin ABvakionopeudella υ 0 , hankittu potentiaalisen eron vaikutuksesta U 0 , mikä elektroni siirtyi kondensaattoriin; 2) tasaisesti kiihdytetty liike pystysuunnassa positiivisesti varautuneeseen levyyn kondensaattorin vakiokenttävoiman vaikutuksesta. Poistuessaan kondensaattorista, elektroni liikkuu tasaisesti nopeudella υ, mitä hänellä oli pisteessä Mlauhduttimesta lähtiessä.
Kuv. 15.4 osoittaa, että haluttu etäisyys | BC | \u003d h 1 + h 2 , missä kanssa h 1 - etäisyys, jolla elektroni siirtyy pystysuunnassa kondensaattorin liikkeen aikana; h 2 - etäisyys näytön pisteen D välillä, johon elektroni putoaa, liikkuessa kondensaattorin poistossa alkuperäisen nopeuden suuntaan υ 0 ja piste C, jossa elektroni todella putoaa.
Ilmaista erikseen h 1 ja h 2 . Käyttämällä kaavaa tasaisesti kiihdytetyn liikkeen polun pituudelle, löydämme
.
(1)
jossa ja- elektronin aikaansaama kiihtyvyys kondensaattorikentän vaikutuksesta; t-elektronien lentoaika kondensaattorin sisällä.
Newtonin toisen lain mukaan a \u003d F / m,jossa F- voima, jolla kenttä vaikuttaa elektroniin; m-sen massa. Vuorostaan F \u003d eE \u003d eU 1 / djossa e- elektronin varaus; U 1 - potentiaaliero kondensaattorin levyjen välillä; d- niiden välinen etäisyys. Löydämme kondensaattorin sisällä olevan elektronin lentoajan yhtenäisen liikepolun kaavasta 
,
mistä alkaen
jossa l 1
- kondensaattorin pituus elektronin lentosuuntaan. Löydämme nopeuden ilmaisun kentän suorittaman työn tasa-arvon olosuhteista liikuttaessa sen hankkimaa elektronia ja kineettistä energiaa: 
.
Täältä
(2)
Korvaavat kaavassa (1) arvot peräkkäin ja,F, tja υ
0 2
vastaavista lausekkeista saamme 
Leikkauspituus h 2 löydämme kolmioiden samankaltaisuudesta MDCja varastossa:
(3)
jossa υ 1 - elektronin nopeus pystysuunnassa pisteessä M;l 2 - etäisyys kondensaattorista näytölle.
nopeus υ 1 löydämme kaavan mukaan υ 1 \u003d klojoka antoi ilmaisut a, Fja ttulee muotoon
Lausekkeen korvaaminen υ
1 kaavalle (3), saamme 
,
tai korvaamalla υ
0 2 kaavan (3) avulla, löydämme
Lopuksi halutulle etäisyydelle BC| | | on
|BC|=
Korvataan määrien arvot U 1 ,U 0 ,d,l 1 ja l 2 viimeiseen lausekkeeseen ja laskelmien tekemiseen, saadaan | BC| \u003d 5,5 cm.
Tehtävät
Pistevarausten kentän potentiaalinen energia ja potentiaali
15.1. Pistevaraus Q\u003d 10 nC, jollakin kentän pisteellä, on potentiaalienergia P \u003d 10 μJ. Etsi kentästä tämän pisteen potentiaalinen φ.
5.2. Kun siirrät latausta Q \u003d 20nCl kentän kahden pisteen välillä ulkoisten voimien toimesta, työ tehtiin A \u003d 4mj. Määritä työ 1 kenttävoimat ja näiden kenttäpisteiden potentiaaliero Δφ.
15.3. Sähkökenttä syntyy pistepisteellä Q 1 \u003d 6 nC Positiivinen varaus Q 2 siirretty pisteestä tämä kenttä pisteeseen (Kuva 15.5). Mikä on potentiaalienergian ΔP muutos siirrettyä latausyksikköä kohti, jos r 1 \u003d 20 cm ja r 2 \u003d 50 cm?
15.4.
Pistevarauksen luoma sähkökenttä Q l \u003d 50 nC. Laske työ, käyttämättä potentiaalin käsitettä sisään 
ulkoiset voimat siirtää pistevarausta Q 2 \u003d -2 nC pisteestä Ckohtaan
(Kuva 15.6), jos r 1 =10 cm, r 2 \u003d 20 cm. Määritä myös varausjärjestelmän potentiaalienergian muutos ΔP.
15.5. Pistevarauksella luotu kenttä Q\u003d 1 nC Määritä kentän potentiaali φ pisteessä, joka on etäisyydellä latauksesta r\u003d 20 cm.
15.6. Määritä sähkökentän potentiaali φ pisteessä, joka on etäällä varauksista Q 1 = 0,2 μC ja Q 2 =0,5 μC, vastaavasti r 1 =15 nähdä ja r 2 \u003d 25 cm. Määritä myös pienin ja suurin etäisyys varausten välillä, joihin ratkaisu on mahdollista.
15.7. maksut Q 1 \u003d 1 μC ja Q 2 = -1 μC ovat etäisyydellä d\u003d 10 cm. Määritä kireys Eja kentän potentiaali φ etäällä olevassa pisteessä r= 10 cm päässä ensimmäisestä latauksesta ja makaa linjalla, joka kulkee ensimmäisen varauksen kohtisuorassa suunnasta alkaen Q 1 - Q 2 .
15.8. Laske kahden pistevarauksen järjestelmän potentiaalienergia P Q 1 \u003d 100 nC ja Q 2 =10 nCl etäisyydellä d\u003d 10 cm: n päässä toisistaan.
15.9. Löydä kolmipistevarausjärjestelmän potentiaalienergia P Q 1 \u003d 10 nC, Q 2 =20 nCl ja Q 3 \u003d -30 nC, joka sijaitsee tasasivuisen kolmion kärkissä, joiden sivupituus on \u003d 10 cm.
15.10. Mikä on neljän samanlaisen pistevarauksen järjestelmän potentiaalienergia P Q\u003d 10 nC, joka sijaitsee sivun pituudeltaan neliön kärkissä ja\u003d 10 cm? .
15.11. Määritä neljän pistevarauksen järjestelmän potentiaalienergia P, joka sijaitsee sivupituuden omaavan neliön kärkissä \u003d 10 cm. Lataukset ovat samanlaisia Q\u003d 10 nC, mutta kaksi niistä on negatiivisia. Harkitse kahta mahdollista tapausta maksujärjestelystä.
15.12
. Kahden pistevarauksen luoma kenttä +
2Qja -Q,etäisyydellä d\u003d 12 cm: n päässä toisistaan. Määritä pisteiden geometrinen sijainti tasossa, jonka potentiaali on nolla (kirjoita nollapotentiaalin viivan yhtälö).
5.13. Järjestelmä koostuu kolmesta varauksesta - kahdesta saman suuruisesta Q 1 = |Q 2 | \u003d 1 μC ja vastapäätä merkissä ja varauksessa Q \u003d 20nC, joka sijaitsee pisteessä 1 järjestelmän kahden muun varauksen välissä (kuva 15.7). Määritä järjestelmän potentiaalienergian ΔP muutos varauksensiirron aikana Qkohdasta 1 pisteeseen 2. Nämä kohdat poistetaan negatiivisesta varauksesta Q 1 etäisyydellä a \u003d0,2 m.
Lineaarisesti jakautuneiden maksujen potentiaalikenttä
15.14. Ohuella säderenkaalla R \u003d10 cm, varaus, jonka lineaarinen tiheys τ \u003d 10 nC / m, jakautuu tasaisesti. Määritä potentiaali φ pisteessä, joka sijaitsee renkaan akselilla etäisyydellä a \u003d5 cm keskustasta.
15.15. Varaus, jonka lineaarinen tiheys on τ \u003d 10 nC / m, jakautuu tasaisesti ohuen suoran johtimen segmenttiin. Laske tämän varauksen luoma potentiaali φ pisteessä, joka sijaitsee johtimen akselilla ja kaukana segmentin lähimmästä päästä etäisyydellä, joka vastaa tämän segmentin pituutta.
Edellisessä kappaleessa keskustelimme sähkökentän pääominaisuudesta - sen voimakkuudesta. Kuten itse määritelmästä seuraa, tämä on tehoominaisuus, ja siksi vektori. Joissakin tapauksissa skalaariominaisuudet ovat kätevämpiä, mikä osoittautuu, että voidaan ottaa käyttöön myös sähköstaattiselle kentälle - potentiaaliero ja potentiaali. Tässä tapauksessa luotamme sähköstaattisen kentän varauksella toimivien voimien tärkeään perusominaisuuteen - niiden konservatiivisuuteen.
Muista, että konservatiiviset voimat ovat niitä, joiden työ ei riipu kehon suuntauksen muodosta. Tällaisten voimien työ määrätään vain siirtymän aloitus- ja loppupisteiden koordinaateilla. Tietojemme perusteella mielivaltaisen varausjärjestelmän luoman sähköstaattisen kentän voimaominaisuuksien ominaisuuksista voimme suorittaa yksityiskohtaisen todistuksen työn tasavertaisuudesta, kun varaus siirtyy minkä tahansa kahden pisteensä välillä. Mutta me pienennämme tätä menettelyä palauttamalla mieleen lause keskusvoimien konservatiivisuudesta, jonka todistimme mekaniikan osiossa.
Kiinteä pistevaraus on "keskusvoimien kentän" lähde - tämä seuraa suoraan sähköstatiikan peruslain - Coulombin lain - muotoilusta. Sähkökenttien superpositioperiaatteesta seuraa, että tämä työ siirretään testivarausta minkä tahansa järjestelmän kentällä lepää maksut on kunkin latauksen kentässä työskentelevän työn algebrallinen summa erikseen. Joten tällaisten joukkojen kenttä (”Coulomb-joukot” *) on myös konservatiivisten voimien kenttä. Tämä vaadittiin todistamaan.
Siten sähkökentän voimien **) työ siirtämällä pisteen (testi) varausta kahden pisteen välillä kuvaa tätä kenttää. Mutta se riippuu myös testilatauksen arvosta q 0. Tämä todistaa kokemus, mutta se on ymmärrettävää ja perustuu tietoihimme "Coulomb" -joukkoista. Loppujen lopuksi ne ovat verrannollisia varaukseen q 0 kullakin radan 1®2 pisteessä (perustuu Coulombin lakiin), ja työ on verrannollinen voimaan. Kenttä ja vain kenttä voidaan karakterisoida jakamalla työ testitulon arvolla. Se, mikä osoittautuu, on "potentiaalinen ero". Annamme määritelmän tälle tärkeälle käsitteelle:
(ODA .) Mahdolliset erot sähköstaattisen kentän 1 ja 2 pisteiden väliin kutsutaan asenne työ kenttä testilatauksen liikkeelle pisteestä1 kohtaan2 tämän latauksen suuruuteen :
. (3.1)
SI-järjestelmässä potentiaalierojen mittayksikköä kutsutaan 1 voltiksi (1 V \u003d 1 J / C). Jos opimme määrittelemään potentiaaliero millään tavalla j 1 –j 2 lepovarausjärjestelmän kentälle (teoreettisesti tai kokeellisesti), tämä mahdollistaa kentän työn löytämisen siirtämällä mitä tahansa piste maksu q tällä alalla:
. (3.2)
Joten potentiaalinen ero on energiaominaisuus sähkökenttä, koska se liittyy suoraan työn käsitteeseen.
Mekaniikassa otimme konservatiivisten voimien (nyt sanomme ”konservatiivisten voimien kentät”) käsitteen ”potentiaalinen energia”. Tässä tapauksessa meitä ohjasi seuraava periaate: "kenttäjoukkojen työ on yhtä suuri kuin potentiaalisen energian menetys". Muodostamme tämän periaatteen analyyttisessä tietueessa:
Tässä U 1 ja U 2 ovat potentiaalienergiaa järjestelmän ”alku” (”1”) ja “lopullinen” (“2”) tilassa. Käsiteltävänä olevassa tapauksessa kiinteiden maksujen järjestelmän kentät ovat pistevarauksen energiaa qasennossa "1" (koordinaateilla ( x 1 ,y 1 ,z 1) ja sijainti “2” (koordinaateilla ( x 2 ,y 2 ,z 2)) sähköstaattinen kenttä. eli potentiaalinen varausenergia tällä kentällä on kentän pisteiden U \u003d U skalaarifunktio x,y,z) (tai). Vertaamalla (3.2) ja (3.3) näemme - on tarkoituksenmukaista olettaa, että potentiaaliero on kenttäpisteiden koordinaattien toisen skalaarifunktion arvojen ero. j(x, y, z). Se liittyy funktioon U ( x,y,z) (potentiaalienergia) yksinkertaisella suhteella: U ( x,y,z) = q× j(x, y, z). Tai sitten
he sanovat, että se on "numeerisesti yhtä suuri kuin yksikön positiivisen varauksen potentiaalinen energia" tietyssä kentän kohdassa. Ja tätä määrää kutsutaan jSähköstaattisen kentän tämän pisteen "potentiaali".
Tärkeintä on, kuinka löytää tämä toiminto tietyn latausjärjestelmän kentälle? Mikä on menettely?
Ensinnäkin, sinun on sovittava normalisointiolosuhteista *): sinun on valittava piste P 0, jossa testivarauspotentiaalin oletetaan olevan nolla. Tällainen piste valitaan useimmiten ”äärettömästi” etäiseksi, jos kenttä puuttuu **). Tätä varten etsi "erityinen" kenttätyö - eli kuljetetun testivarauksen arvoon (tai kuten usein sanotaan, "yksikön positiivisen varauksen siirtäminen") liittyvä työ tietystä kentän pisteestä P(x,y,z) normalisointipisteeseen P 0. Analyyttisessä muodossa tämä määritelmä potentiaali voidaan kirjoittaa näin:
(Def. ) j P(x,y,z) = . (3.5)
Onko mahdollista ilmaista arvot, jotka olemme ottaneet uudelleen käyttöön - potentiaaliero ja potentiaali voiman ominaispiirteellä, jonka olemme jo oppineet laskemaan annetusta tilauksen varaustilanteesta? Tietysti voit. Me kirjoitamme ymmärrettävän tasa-arvoketjun:
.
Kirjoitamme viimeisen tasa-arvon uudelleen
. (3.6)
Se antaa ”reseptin” potentiaalierojen etsimiseksi tunnetulla intensiteettifunktion avulla. Samoin potentiaalin suhteen:
Ja lopuksi kentän mielivaltaisen pisteen potentiaalista P koordinaateilla ( x,y,z):
. (3.7)
· Pistevarauskentän potentiaali
Potentiaalin laskentamenetelmän perusteella saadaan lauseke pistevarauksen kentän tapauksessa. Tämä on erittäin tärkeää avaruudessa mielivaltaisesti sijaitsevan varausjärjestelmän kenttäpotentiaalin laskemiseksi edelleen.
2. Radan valinta. Anna mielivaltainen kohta P(x,y,z) on etäisyydellä rlatauslähteestä. Koska tulos ei riipu muodon (3.7) kaarevan integroinnin laskemisessa kulkevasta suuntauksesta, valitsemme yksinkertaisimman säteittäisesti suunnatun suoran kentän tietystä kohdasta kenttäviivaa pitkin ja "menemme äärettömyyteen".
3. laskelma. Potentiaalin määritelmän mukaisesti lasketaan pistemaksulla luodun kentän "erityinen" työ qtestivarauksen siirrosta valittua rataa pitkin. Alla oleva tasa-arvoketju, toivottavasti, näyttää melko ”avoimelta”. Annamme kuitenkin siitä minimaalisen kommentin. Ensinnäkin panemme merkille, että koska olemme valinneet suuntauksen radalta säteittäisesti suunnatun palkin muodossa, voimme kirjoittaa E lja dl(mielivaltainen käyrä " L») Vaihda kohtaan Er ja dr(napa-akseli " r"). Lisäksi, koska vektori on suunnattu radiaalisesti, jokaiselle pienelle siirtymälle suunnassa, intensiteettivektorin projektio on yksinkertaisesti yhtä suuri kuin tämän vektorin moduuli E(r). Seurauksena on, että voimme ottaa tärkeän askeleen laskelmassamme - tehdä siirtyminen kaarevasta integraalista tavalliseen määriteltyyn:
.*)
Nyt korvaamalla lauseke pistevarauksen kenttävoimakkuuden moduulilla (3.5), meillä on vain matemaattinen ”rutiini”:
Kirjoitetaan tulos uudelleen, täydentämällä sitä läpäisevyydellä kaasumaisen tai nestemäisen homogeenisen dielektrisen väliaineen mahdollisella läsnäololla ejoka täyttää pistevarausta ympäröivän tilan:
. (3.8)
Pistevarauksen kentän potentiaali, kuten näemme, pienenee etäisyyden kanssa lain mukaan 1 / r.
· Potentiaalipotentiaaliset pinnat
Keskustellessamme sähköstaattisen kentän voimaominaisuuksista vakuutimme voimalinjojen (jännitysviivojen) käsitteen hedelmällisyydestä. Kentän energiaominaisuuksien - potentiaalin - kannalta on hyödyllistä ottaa käyttöön myös havainnollistava lisäominaisuus - "potentiaalipotentiaalisten pintojen" järjestelmä. Itse nimestä on selvää (“equi” tarkoittaa “yhtä”), että nämä ovat vakiopotentiaalisia pintoja, jotka kuvaavat kenttävoimien kykyä toimia, kun varaus liikkuu. Tällaisten pintojen varrella työtä ei tietenkään tehdä ollenkaan. Se on suurin suuntiin, joissa potentiaalisten potentiaalisten pintojen järjestelyn tiheys (tiheys) on suurin. Näissä paikoissa suurin kentänvoimakkuus. On helppo selvittää, mikä voimajohtojen ja potentiaalisten potentiaalisten pintojen keskinäinen orientaatio on niiden leikkauspisteissä: ne ovat keskenään kohtisuorassa. Tosiasiassa jokaiselle pienelle siirtymälle potentiaalipotentiaalista pintaa kohden alkutyö on yhtä suuri kuin nolla, ja tämä on mahdollista vain, jos jännitysvektorin tangenttikomponentti on nolla, ts. se on suunnattu tiukasti normaaliin pintaan. Alla annamme ketjun, joka vastaa näitä sanoja, toivottavasti melko selviä yhtäläisyyksiä:
Yhdessä viikunan kanssa 3. ... ne todistavat jo muotoillun lausunnon: voimajohdot ylittävät (tai "sopii ...") potentiaalipotentiaaliset pinnat suorassa kulmassa !
Annamme kuvan potentiaalisista potentiaalipinnoista (ja myös kenttälinjoista) joillekin tuttuihin sähköstaattisen kentän yksinkertaisimpiin tapauksiin: ja) pistevarauksen kenttä; b) kahden samanlaisen modulo-vastakkaispistevarauksen kenttä; sisään) kenttä kahden vastakkaisesti ladatun tasasuuntaisen suuren (verrattuna niiden väliseen etäisyyteen) levyjen välillä - katso kuva. 3.1.