§ 12.3 Voimien toiminta sähköstaattinen kenttä. Potentiaalia. Potentiaalipotentiaaliset pinnat
Voima q pr, joka on sijoitettu mielivaltaiseen kohtaan sähköstaattisessa kentässä intensiteetillä E, vaikuttaa voimalla F \u003d q pr E. Jos varausta ei ole kiinteä, voima aiheuttaa sen liikkumisen ja siksi työ tehdään. Alkuperäinen työ, jonka voima F suorittaa siirtämällä pisteen sähkövarausta q pr sähkökentän a kohdasta pisteeseen b polun dℓ segmentillä, määritelmän mukaan on yhtä suuri kuin
(α on kulman F ja liikesuunnan välinen kulma) (kuva 12.13).
Jos työn tekevät ulkoiset voimat, niin dA< 0 , если силами поля, то dA > 0. Viimeisen lausekkeen integroimalla saadaan työ kenttävoimia vastaan \u200b\u200bliikuttaessa q CR: tä pisteestä kohtaan b
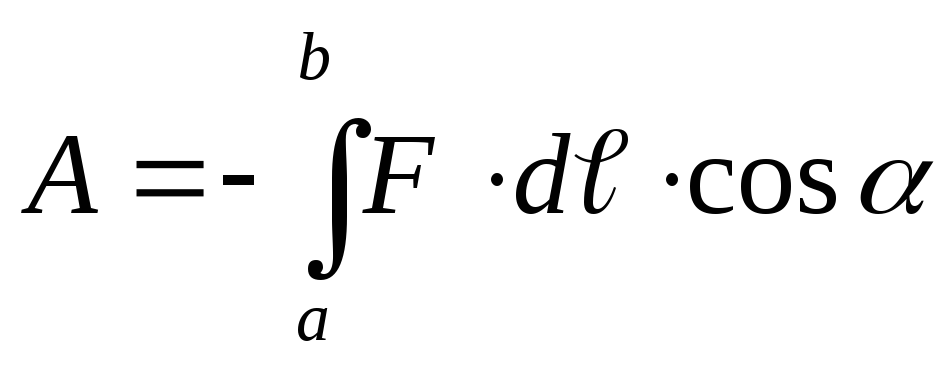(12.20)
Kuva -12,13
(
- Coulomb-voima, joka vaikuttaa testivaraukseen q pr kentän jokaisessa pisteessä intensiteetillä E).
Sitten työskentele
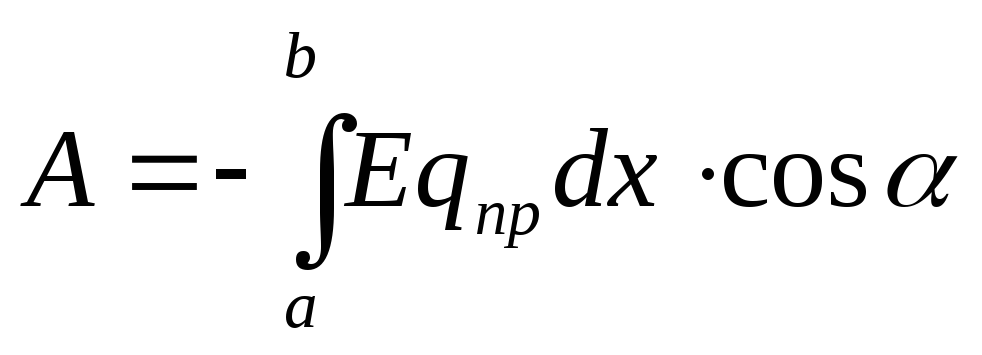(12.21)
Liike on kohtisuora vektoriin nähden 
, siksi cosα \u003d 1, testilatauksen q CR siirron työ että b on yhtä suuri kuin
(12.22)
Sähkökenttävoimien työ varauksen liikkuessa ei riipu polun muodosta, vaan riippuu vain suuntauksesta, jolla lähtöpiste ja loppupiste ovat suhteessa toisiinsa.
Niinpä pistevarauksen sähköstaattinen kenttä onmahdollinen ja sähköstaattiset voimat -konservatiivinen .
Tämä on potentiaalisten kenttien ominaisuus. Tästä seuraa, että suljetun silmukan sähkökentässä suoritettu työ on nolla:
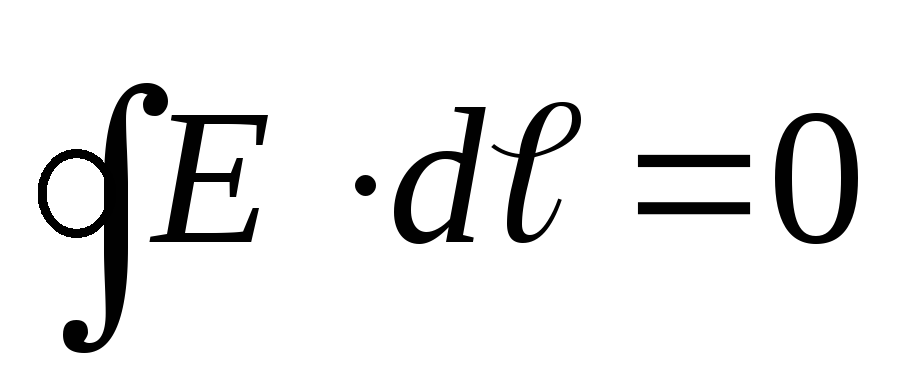(12.23)
olennainen 
sitä kutsutaan vetovektorin kierto
. Vektorin E kiertonopeuden nollaamisesta seuraa, että sähköstaattisen kentän voimakkuuden viivoja ei voida sulkea, ne alkavat positiivisilla ja päättyvät negatiivisilla varauksilla.
Kuten tiedät, konservatiivisten voimien työ suoritetaan potentiaalisen energian menetyksen vuoksi. Siksi sähköstaattisen kentän voimien työ voidaan esittää potentiaalienergioiden erona, joka pistevarauksella q pr on varauskentän q alku- ja loppupisteissä:
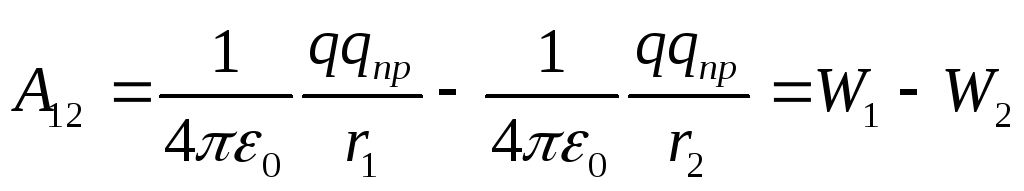(12.24)
mistä seuraa, että varauksen q CR potentiaalienergia latausalueella q on
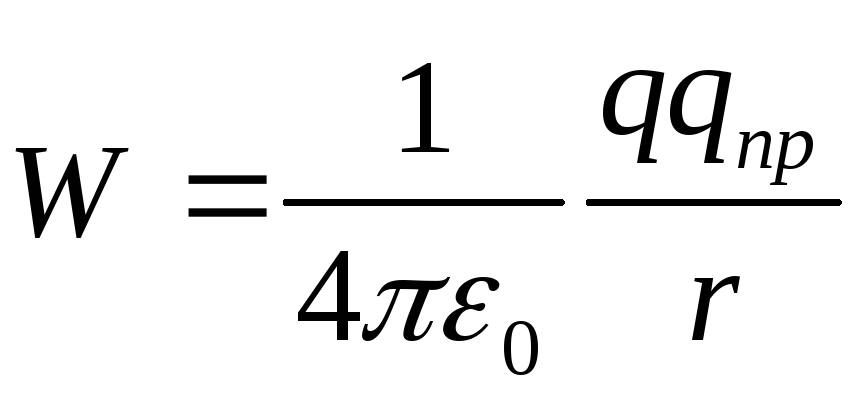(12.25)
Samoilla varauksilla q pr q\u003e 0 ja niiden vuorovaikutuksen (heijastus) potentiaalienergia on positiivinen, toisin kuin varauksissa q pr q< 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Jos kenttä on luotu n-pistejärjestelmän avulla, veloitetaan q 1, q 2, .... q n, tässä kentässä sijaitsevan varauksen q ol potentiaalienergia U on yhtä suuri kuin sen kunkin varauksen erikseen luoman potentiaalienergian U i summa:
(12.26)
asenne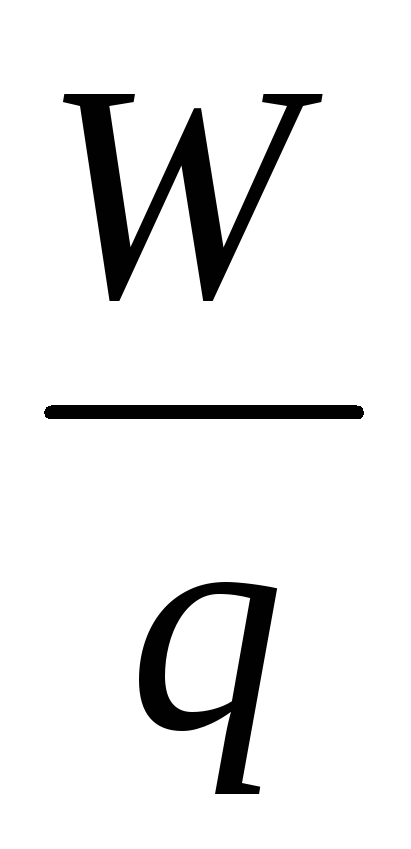 
ovat riippumattomia varauksesta q ja ovat sähköstaattisen kentän energiaominaisuus.
Skaalaarista fysikaalista määrää, mitattuna sähköstaattisessa kentässä olevan testivarauksen potentiaalienergian suhteella tämän varauksen arvoon, kutsutaan sähköstaattinen kenttäpotentiaali.
(12.27)
Pistevarauksen q luoman kentän potentiaali on
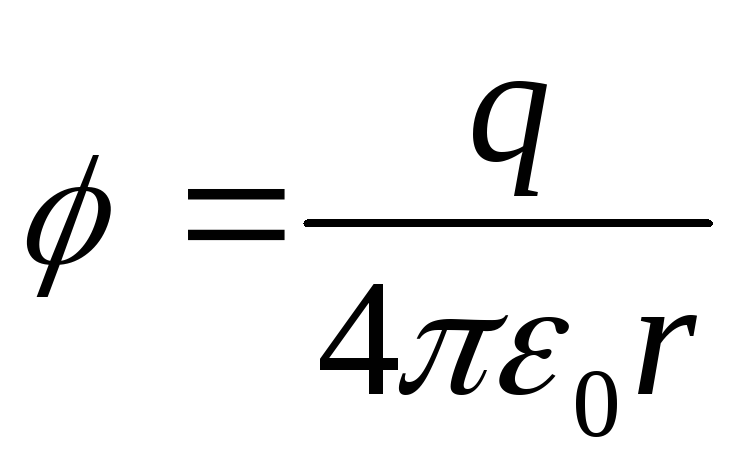(12.28)
Mahdollisuusyksikkö - voltti.
Sähköstaattisen kentän voimien suorittama työ siirtäessä varausta q ol pisteestä 1 pisteeseen 2 voidaan esittää
eli yhtä suuri kuin siirretyn varauksen tulo potentiaalierolla lähtö- ja lopetuspisteissä.
Sähköstaattisen kentän kahden pisteen φ 1 -φ 2 potentiaaliero on yhtä suuri kuin jännite. sitten
Sähköstaattisen kentän suorittaman työn suhdetta siirtäessä testivarausta kentän yhdestä pisteestä toiseen tämän varauksen arvoon kutsutaanjännite näiden kohtien välillä.
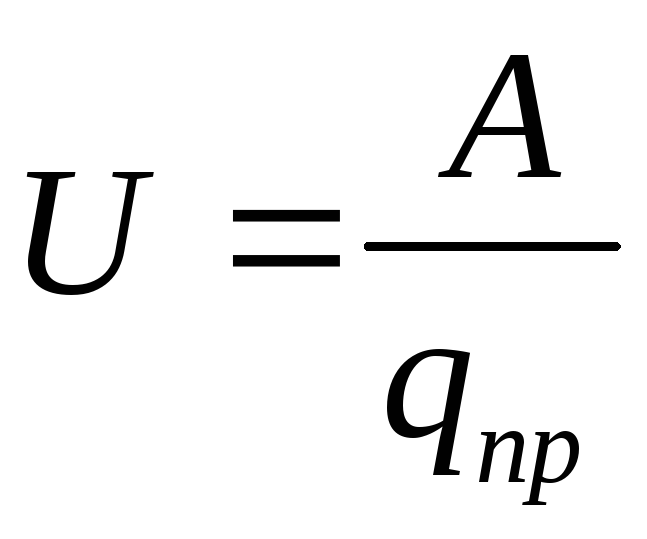(12.30)
Graafisesti sähkökenttä voidaan kuvata paitsi jännitysviivojen avulla myös potentiaalipotentiaalien avulla.
potentiaalintasaus pinta - joukko pisteitä, joilla on sama potentiaali. Kuviosta voidaan nähdä, että jännitysviivat (radiaalisäteet) ovat kohtisuorassa potentiaalisten potentiaalisten viivojen kanssa.
E 
lukemattomia potentiaalisia pintoja jokaisen varauksen ympärillä ja kukin varausjärjestelmä voi piirtää lukemattomia sarjoja (kuva 12.14). Ne kuitenkin suoritetaan siten, että kahden vierekkäisen potentiaalipotentiaalin väliset potentiaalierot ovat samat. Sitten potentiaalisten potentiaalisten pintojen tiheys kuvaa visuaalisesti kentänvoimakkuutta eri kohdissa. Jos nämä pinnat ovat tiheämpiä, kentän voimakkuus on suurempi. Tietäessä potentiaalisten potentiaalisten viivojen (pintojen) sijaintia, on mahdollista rakentaa vetoviivoja tai tunnetusta vetojohtojen järjestelystä on mahdollista rakentaa potentiaalisesti potentiaalisia pintoja.
§ 12.4Jännityksen ja potentiaalin suhde
Sähköstaattisella kentällä on kaksi ominaisuutta: teho (jännitys) ja energia (potentiaali). Jännitys ja potentiaali ovat saman kenttäpisteen eri ominaisuuksia, joten niiden välillä on oltava yhteys.
Yhden pisteen positiivisen varauksen siirtäminen pisteestä toiseen x-akselia pitkin edellyttäen, että pisteet ovat äärettömän lähellä toisiaan ja x 1 - x 2 \u003d dx, on yhtä suuri kuin qЕ x dx. Sama työ on q (φ 1 - φ 2) \u003d -dφq. Vastaten molemmat lausekkeet, voimme kirjoittaa
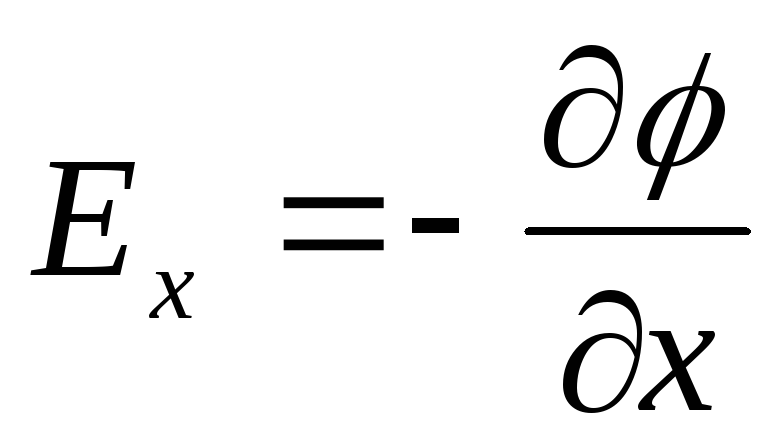
Toistamalla samanlaisia \u200b\u200bhuomioita y- ja z-akseleille, voimme löytää vektorin 
:
jossa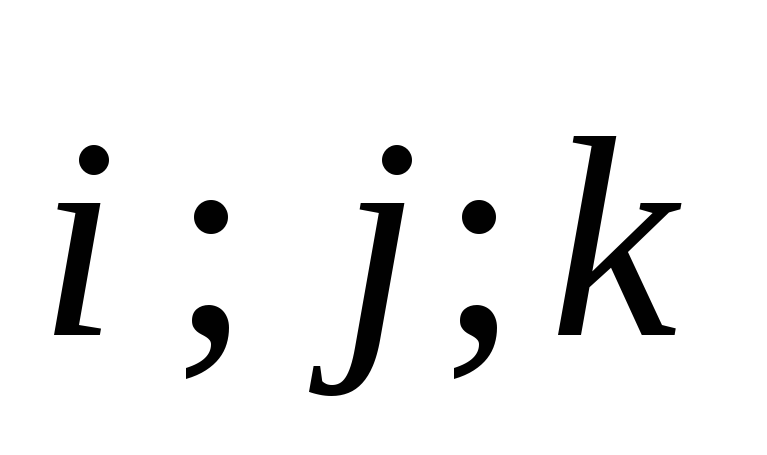 
ovat koordinaattiakselien x, y, z yksikkövektorit.
Kaltevuuden määritelmästä seuraa, että
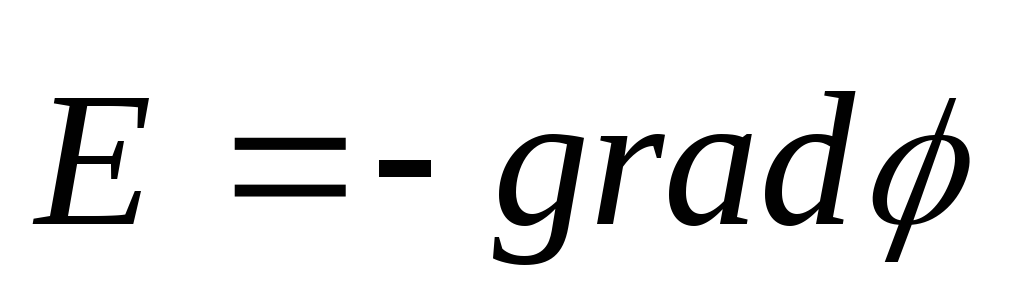tai 
(12.31)
eli kentänvoimakkuus E on yhtä suuri kuin potentiaaligradientti miinusmerkillä. Miinusmerkki merkitsee se, että jännitysvektoriE Kenttä on suunnattu laskevaan potentiaaliin.
Vakiintuneen intensiteetin ja potentiaalin välinen suhde antaa mahdollisuuden löytää potentiaaliero tämän kentän kahden mielivaltaisen pisteen välillä tunnetusta kenttävoimakkuudesta.
Tasaisesti varautuneen pallon kenttä sädeR
Pallon ulkopuolella oleva kenttävoimakkuus määritetään kaavalla
(r\u003e R)
Pisteiden r1 ja r2 (r1\u003e R; r2\u003e R) välinen potentiaaliero määritetään suhteella
Pallopotentiaali saadaan, jos r 1 \u003d R, r 2 → ∞:
Tasaisesti ladatun äärettömän pitkän sylinterin kenttä
Kenttävoimakkuus sylinterin ulkopuolella (r\u003e R) määritetään kaavalla
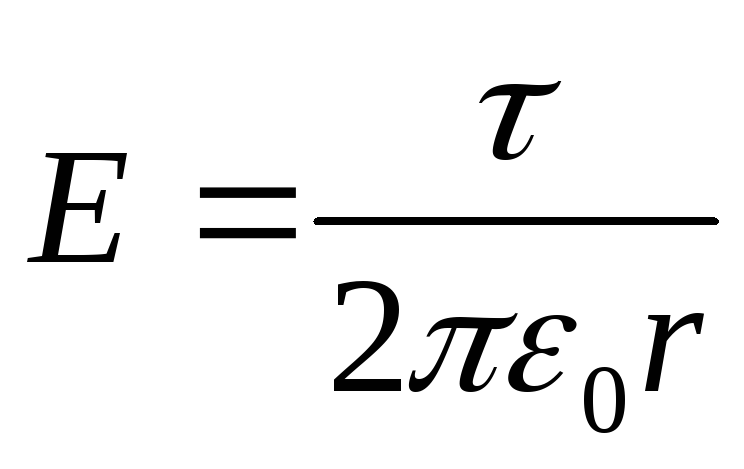
(τ on lineaarinen tiheys).
Kahden pisteen, jotka ovat etäisyydellä r 1 ja r 2 (r 1\u003e R; r 2\u003e R) sylinterin akselilta, potentiaaliero on
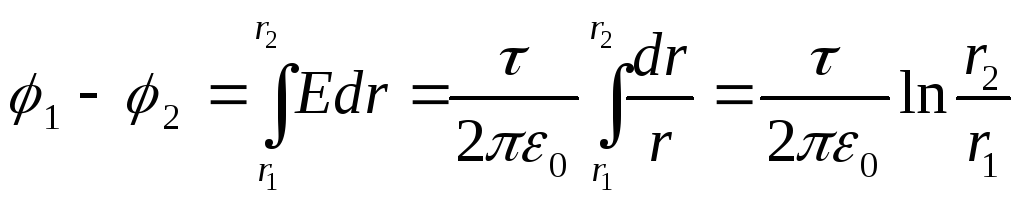(12.32)
Tasaisesti varautuneen ääretön tason kenttä
Tämän tason kenttävoimakkuus määritetään kaavalla
(σ on pinnan tiheys).
X 1: n ja x 2: n etäisyydellä tasosta sijaitsevien pisteiden potentiaaliero on
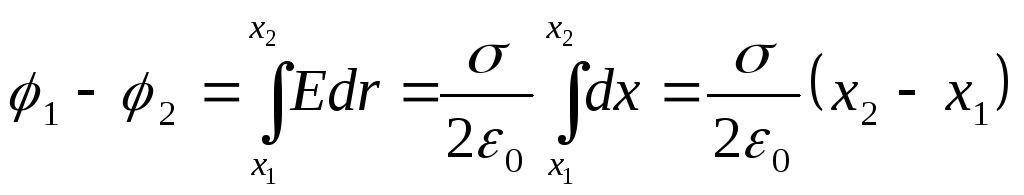(12.33)
Kahden vastakkaisesti ladatun ääretön yhdensuuntaisen tason kenttä
Näiden tasojen kenttävoimakkuus määritetään kaavalla
Koneiden potentiaaliero on
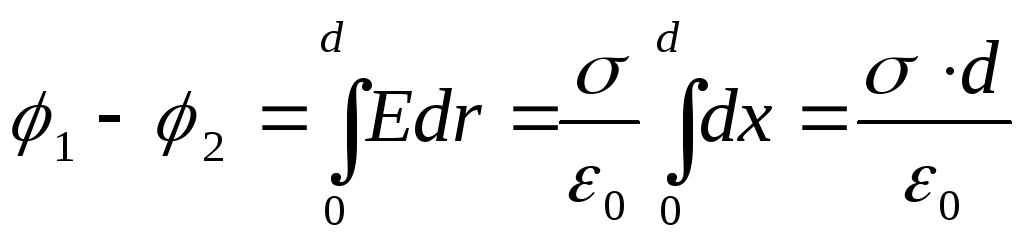(12.34)
(d on tasojen välinen etäisyys).
Esimerkkejä ongelmien ratkaisemisesta
Esimerkki 12.1 . Kolmen pisteen varaukset Q 1 \u003d 2nC, Q 2 \u003d 3nC ja Q 3 \u003d -4nC sijaitsevat tasasivuisen kolmion kärkissä, joiden pituus on sivu \u003d 10 cm. Määritä tämän järjestelmän potentiaalienergia.
Dano : Q1 \u003d 2nC \u003d 2 - 10 - 9 C; Q2 \u003d 3nCl \u003d 3 - 10-9 ° C; ja Q3 \u003d -4nCl \u003d 4 - 10 -9 ° C; \u003d 10 cm \u003d 0,1 m.
Löydä : U.
P 
ratkaisu:
Latausjärjestelmän potentiaalienergia on yhtä suuri kuin kunkin vuorovaikutuksessa olevan varausparin vuorovaikutusenergioiden algebrallinen summa, ts.
U \u003d U 12 + U 13 + U 23
jossa vastaavasti yhden varauksen potentiaalienergiat, jotka sijaitsevat toisen etäisyyden latauksen kentässä ja häneltä ovat tasa-arvoisia
;
;
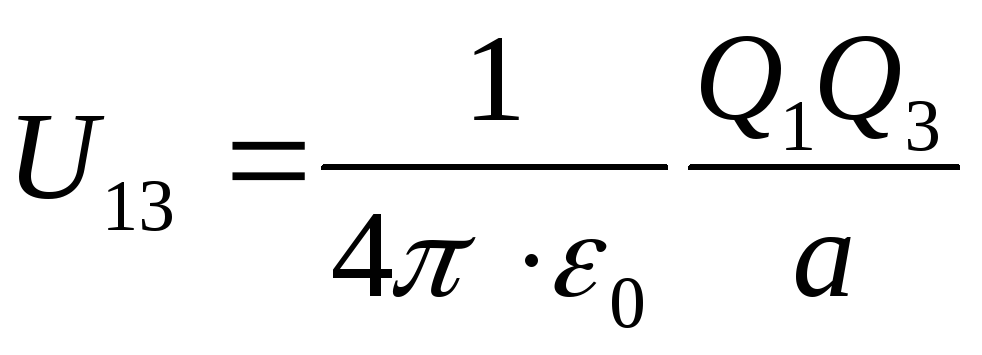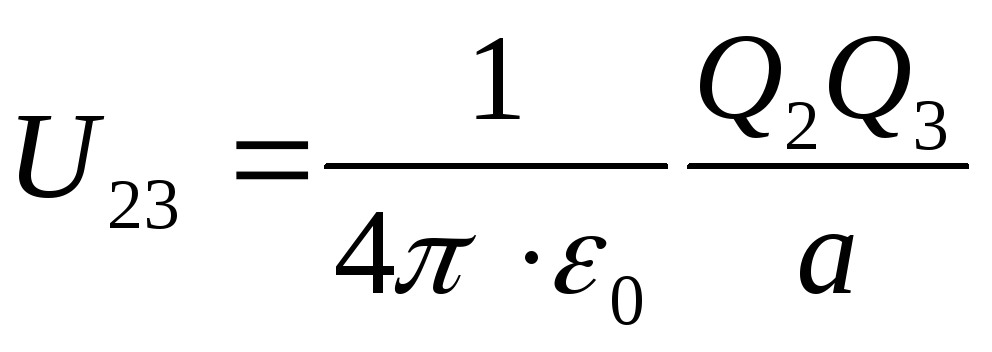(2)
Korvaamme kaavat (2) lausekkeeseen (1), löydämme varausjärjestelmän halutun potentiaalienergian
Vastaus on: U \u003d -0,126 μJ.
Esimerkki 12.2 . Määritä potentiaali renkaan keskellä sisäisellä säteellä R 1 \u003d 30 cm ja ulkoisella säteellä R 2 \u003d 60 cm, jos varaus q \u003d 5 nC on jakautunut tasaisesti siihen.
ilmoittautua: R1 \u003d 30 cm \u003d 0,3 m; R2 \u003d 60 cm \u003d 0,6 m; q \u003d 5nC \u003d 5 - 10 - 9 ° C
Löydä : φ .
ratkaisu: Jaamme renkaan kontsentrisiin, äärettömän ohuisiin renkaisiin, joiden sisäsäde on r ja ulompi (r + dr).
Tarkasteltavana olevan ohuen renkaan pinta-ala (katso kuva) dS \u003d 2πrdr.
P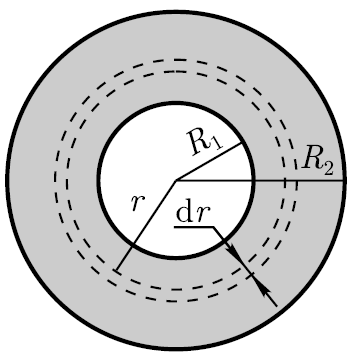 
äärettömän ohuen renkaan luomat renkaan keskellä olevat potentiaalit,
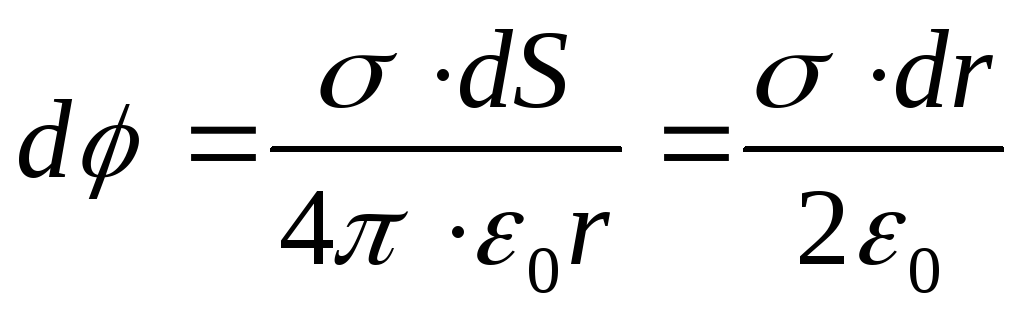
missä on pinnan varaustiheys.
Potentiaalin määrittämiseksi renkaan keskellä meidän on lisättävä aritmeettisesti dφ kaikista äärettömän ohuista renkaista. sitten
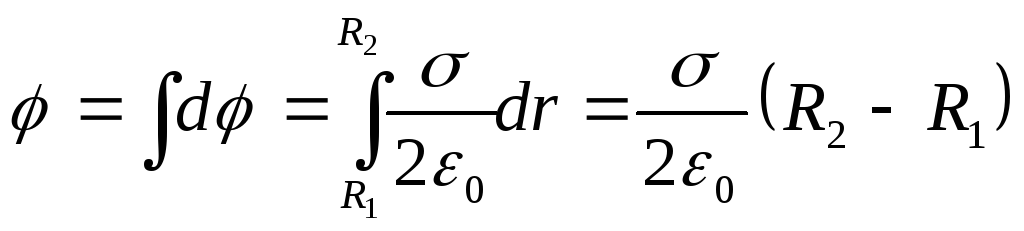
Kun otetaan huomioon, että renkaan varaus on Q \u003d σS, missä S \u003d π (R2 2-R 1 2) on renkaan pinta-ala, saadaan haluttu potentiaali renkaan keskelle
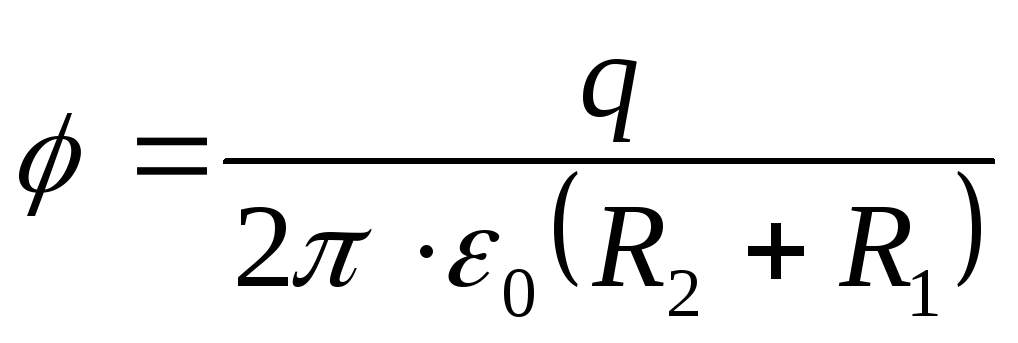
Vastaus : φ \u003d 25 V
Esimerkki 12.3 Kaksi saman nimisen pistepistettä (q 1 \u003d 2nC jaq 2 \u003d 5 nC) ovat tyhjössä etäältär 1 \u003d 20cm. Tunnista työ A, joka on tehtävä niiden saattamiseksi lähemmäksi etäisyyttär 2 \u003d 5 cm.
ilmoittautua: q 1 \u003d 2nC \u003d 2+ 10 - 9 ° C; q 2 \u003d 5nC \u003d 5+ 10 - 9 ° C ; r 1 \u003d 20 cm \u003d 0,2 m;r 2 \u003d 5cm \u003d 0,05m.
Löydä : A.
ratkaisu: Sähköstaattisen kentän voimien suorittama työ, kun varaus Q siirretään kentän pisteestä potentiaalilla φ 1 pisteeseen, jonka potentiaali φ 2.
A 12 \u003d q (φ 1 - φ 2)
Kun saman nimisen lataukset lähentyvät, ulkoiset voimat tekevät työtä, siksi näiden joukkojen työ on yhtä suuri kuin suuresti, mutta merkillä vastakkainen kuin Coulomb-joukkojen työ:
A \u003d -q (φ 1 - φ 2) \u003d q (φ 2 - φ 1). (1)
Sähköstaattisen kentän pisteiden 1 ja 2 potentiaalit
;
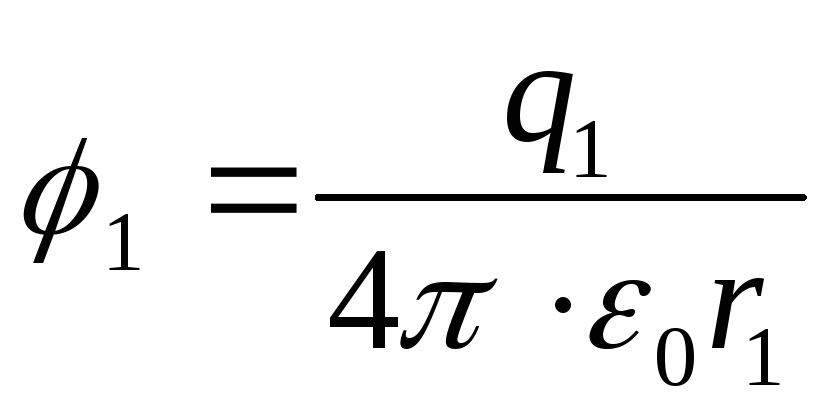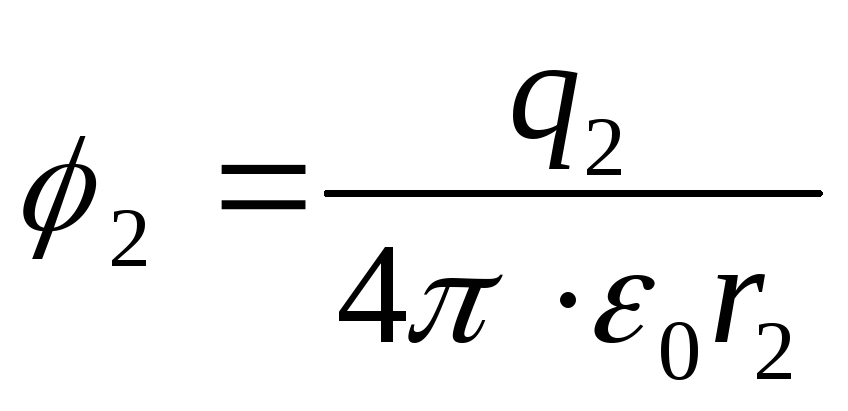(2)
Korvaamalla kaavat (2) lausekkeeseen (1), löydämme halutun työn, joka on tehtävä, jotta lataukset lähentyisivät,
Vastaus on: A \u003d 1,35 μJ.
Esimerkki 12.4. Sähköstaattinen kenttä luodaan positiivisesti varautuneella loputtomalla kierteellä. Protoni, joka liikkuu sähköstaattisen kentän vaikutuksesta hehkulangan jännityslinjaa pitkin etäältär 1 \u003d 2cm -r 2 \u003d 10cm, muutti nopeuttaanυ 1 \u003d 1 mm / s -υ 2 \u003d 5Mm / s. Määritä hehkulangan lineaarinen tiheys τ.
ilmoittautua: q \u003d 1,6 - 10 - 19 ° C; m \u003d 1,67 - 10 - 27 kg; r1 \u003d 2 cm \u003d 2 - 10 -2 m; r2 \u003d 10 cm \u003d 0,1 m; r 2 \u003d 5 cm \u003d 0,05 m; υ 1 \u003d 1Mm / s \u003d 1 - 106 m / s; korkeintaan υ 2 \u003d 5Mm / s \u003d 5 ∙ 10 6 m / s.
Löydä : τ .
ratkaisu: Sähköstaattisen kentän voimien suorittamaa työtä, kun protoni siirtyy potentiaalin potential 1 kentäpisteestä pisteeseen, jonka potentiaali on φ 2, käytetään protonin kineettisen energian lisäämiseen
q (φ 1 - φ 2) \u003d ΔТ (1)
Hehkulangan tapauksessa sähköstaattisella kentällä on aksiaalinen symmetria, siksi
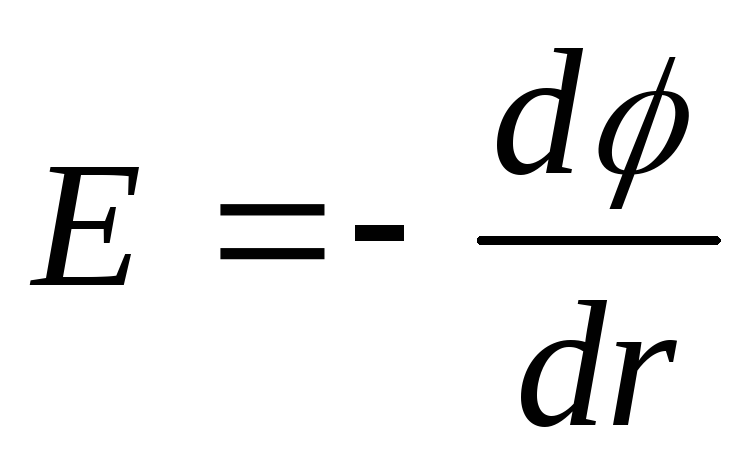tai dφ \u003d -Edr,
sitten potentiaaliero kahden pisteen välillä, jotka sijaitsevat etäisyydellä r 1 ja r 2 langasta,
(otimme huomioon, että tasaisesti varautuneen äärettömän langan luoman kentän intensiteetti,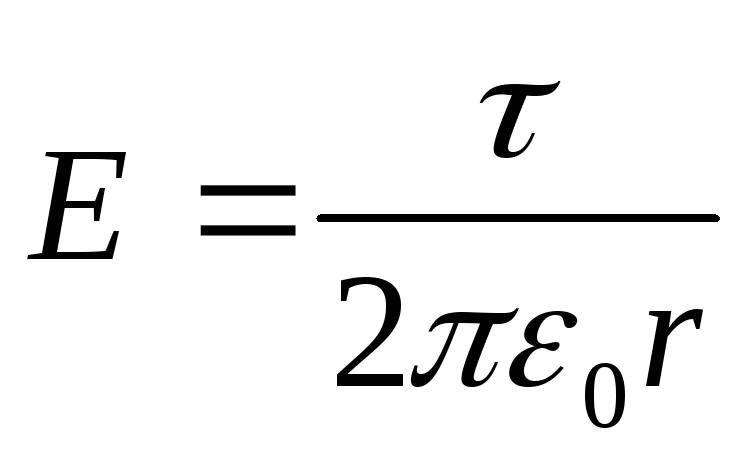 
).
Korvataan lauseke (2) kaavaan (1) ja otetaan huomioon se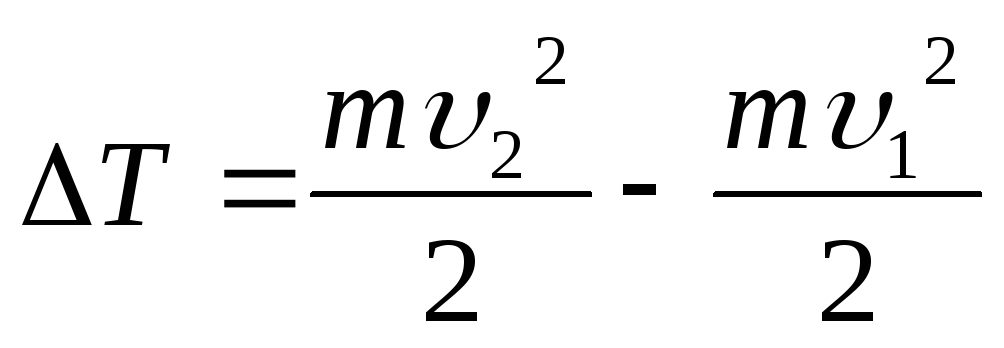 
saamme
Mistä hehkulangan haluttu lineaarinen varaustiheys tulee?
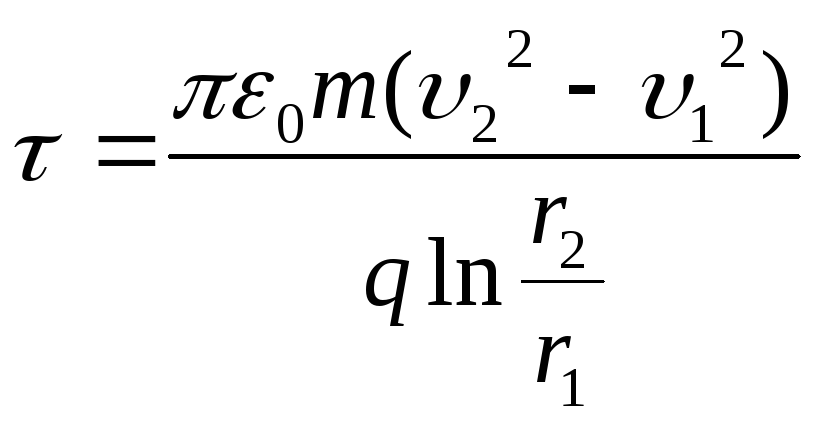
Vastaus : t \u003d 4,33 μC / m.
Esimerkki 12.5. Sähköstaattinen kenttä luodaan tyhjössä sädekuulan avullaR\u003d 8 cm, tasaisesti ladattu irtotiheydellä ρ \u003d 10nC / m 3 . Määritä potentiaaliero tämän kentän kahden pisteen välillä, jotka ovat etäisyydellä pallon keskipisteestä: 1)r 1 \u003d 10cm jar 2 \u003d 15 cm; 2)r 3 \u003d 2cm jar 4 \u003d 5cm ..
ilmoittautua: R \u003d 8 cm \u003d 8 x 10 -2 m; ρ \u003d 10 nC / m 3 \u003d 10 - 10 - 9 nC / m3; r1 \u003d 10 cm \u003d 10 - 10 -2 m;
r 2 \u003d 15 cm \u003d 15 - 10 -2 m; r3 \u003d 2 cm \u003d 2 - 10 -2 m; r 4 \u003d 5 cm \u003d 5 x 10 -2 m.
Löydä : 1) φ 1 - φ 2 ; 2) φ 3 - φ 4 .
ratkaisu: 1) Potentiaaliero kahden pisteen välillä, jotka sijaitsevat r 1: n ja 2: n etäisyydellä pallon keskipisteestä.
(1)
jossa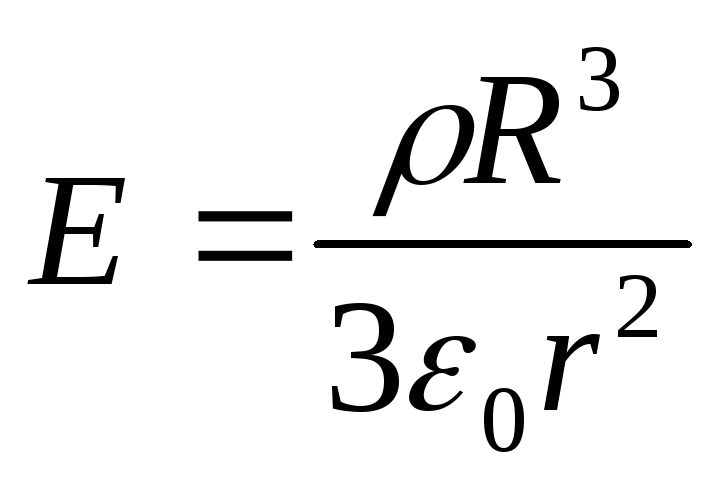 
on kenttävoimakkuus, jonka muodostaa pallo, jolla on tasaisesti varautunut massatiheys ρ missä tahansa pisteessä, joka sijaitsee pallon ulkopuolella etäisyydellä r sen keskustasta.
Korvaamalla tämä lauseke kaavaan (1) ja integroimalla saadaan haluttu potentiaaliero
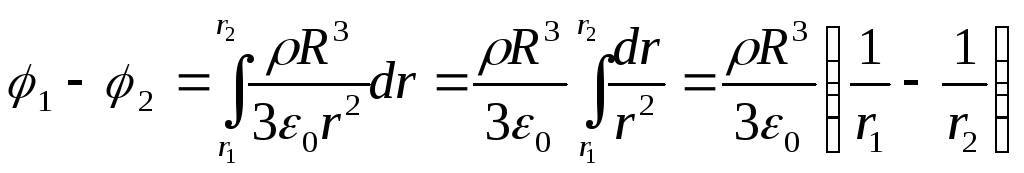
2) potentiaaliero kahden pisteen välillä, jotka sijaitsevat etäisyydellä r 3 ja r 4 pallon pallon keskustasta,
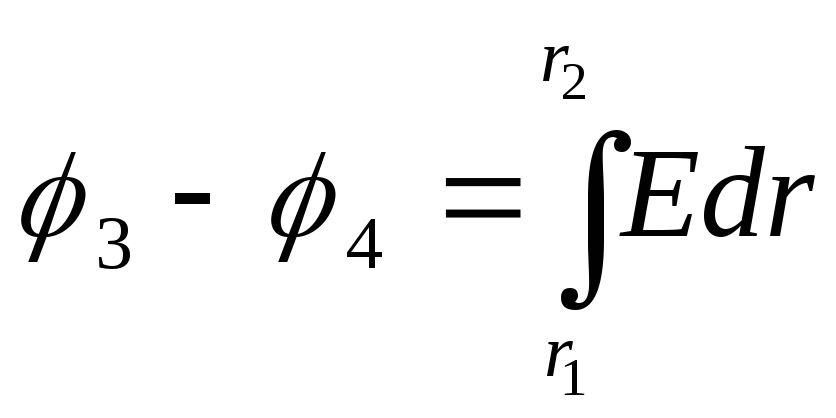(2)
jossa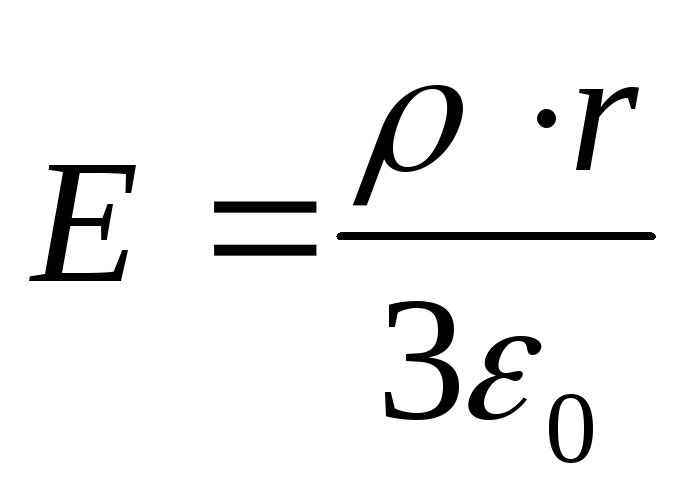 
on kentänvoimakkuus, jonka muodostaa pallo, joka on tasaisesti varautunut massatiheydellä ρ missä tahansa pisteessä, joka sijaitsee pallon sisällä etäisyydellä r sen keskustasta.
Korvaamalla tämä lauseke kaavaan (2) ja integroimalla saadaan haluttu potentiaaliero
Vastaus : 1) 1 - 2 \u003d 0,643 V; 2) 3-3 - 4 \u003d 0,395 V
Latauksen luomien sähkökentän voimien työ varauksen siirtämiseksi 
pisteestä 1 pisteeseen 2 on yhtä suuri kuin:
.
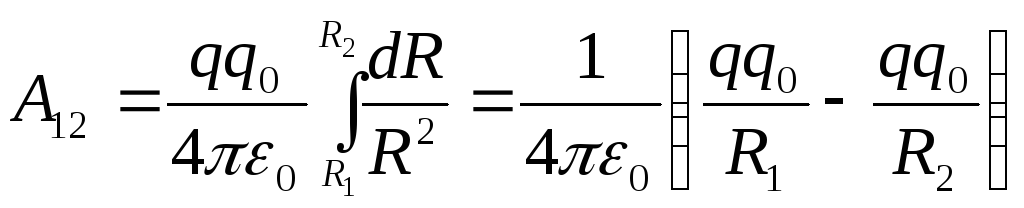Konservatiivisen kentän voimien työ on yhtä suuri kuin potentiaalisen energian menetys:
,
sitten potentiaalinen varausenergia vastaava kenttä 
on yhtä suuri kuin:
.
Vakion arvo valitaan siten, että kun varaus poistetaan äärettömyyteen (ts. Milloin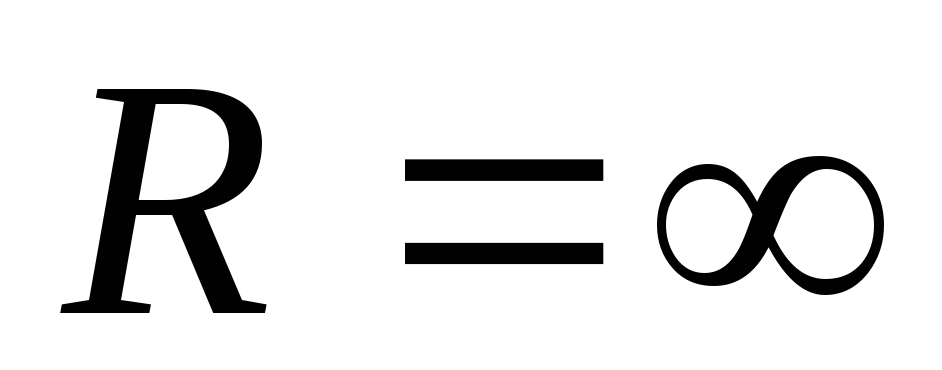 
) potentiaalinen energia katoaisi siis
.
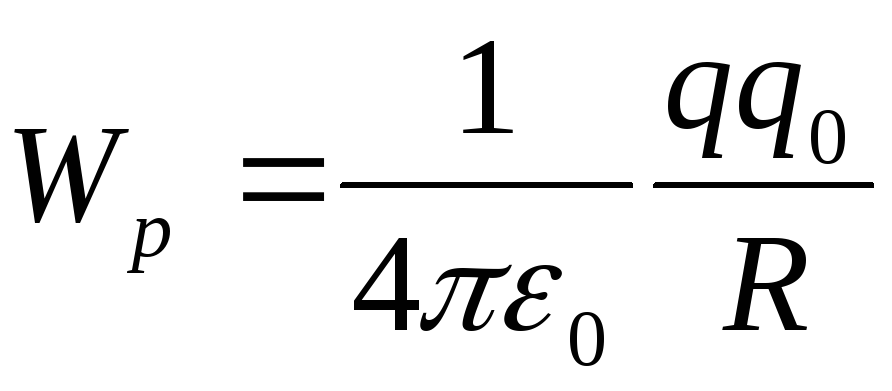On selvää, että eri testimaksut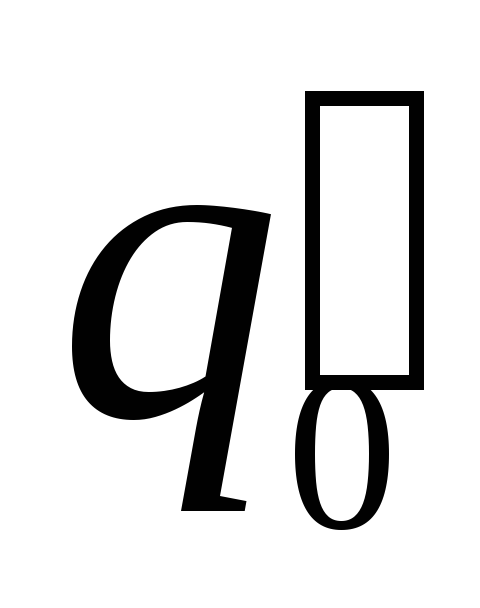 
ja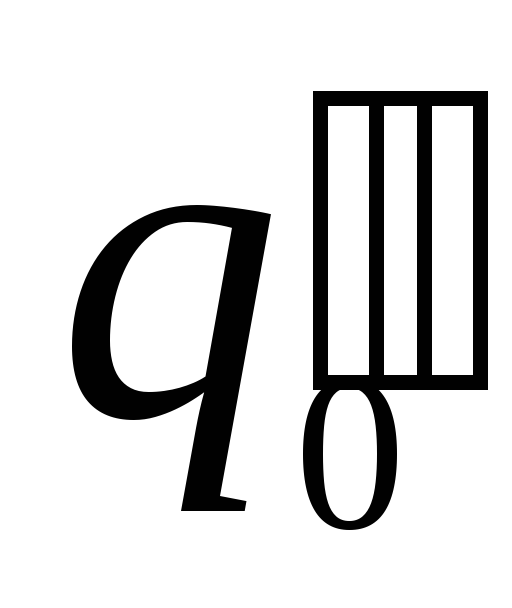 
samassa kentässä on erilainen potentiaalienergia 
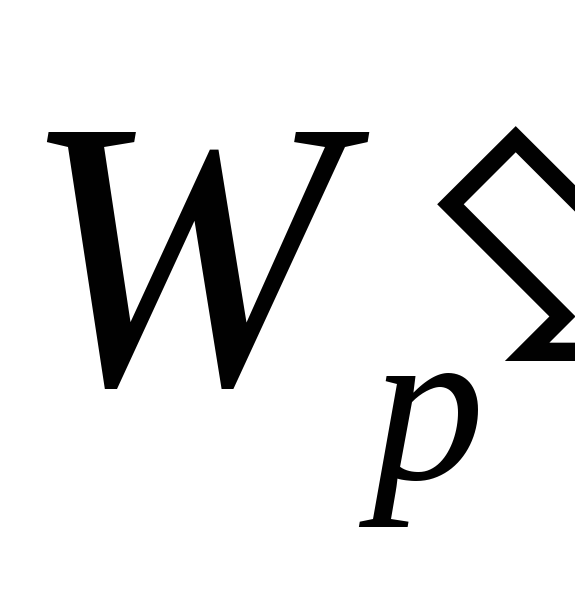ja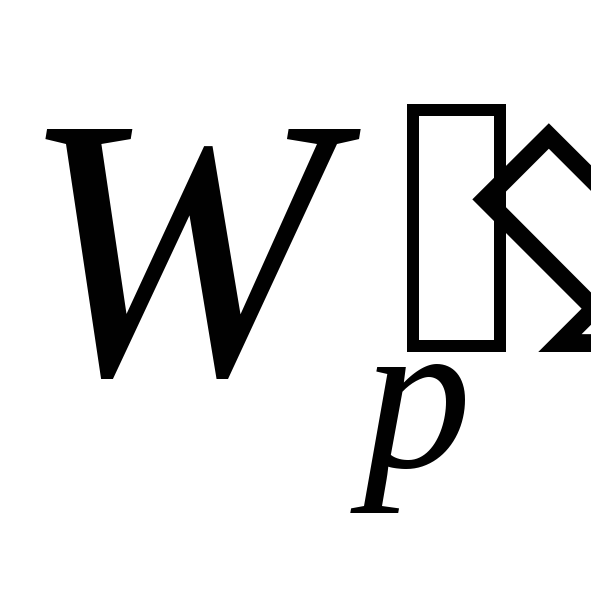 
. Kuitenkin asenne 
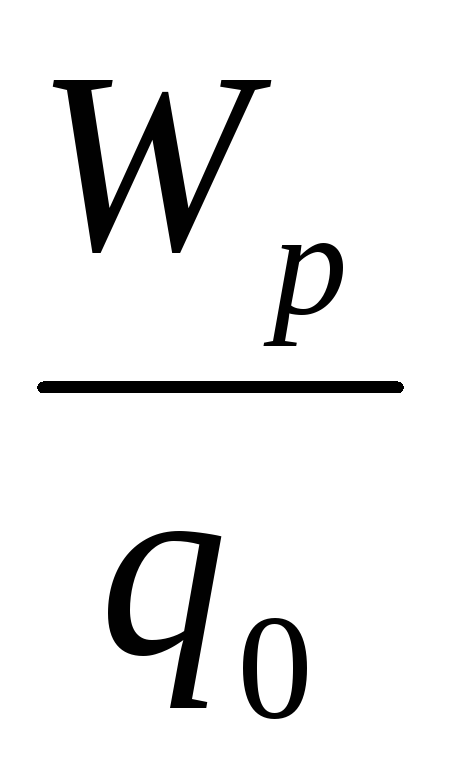kaikille testimaksut ovat samat. arvo
kutsutaan sähkökentän potentiaaliksi ja on sen energiaominaisuus. Pistevarauksen kentän potentiaali on
.
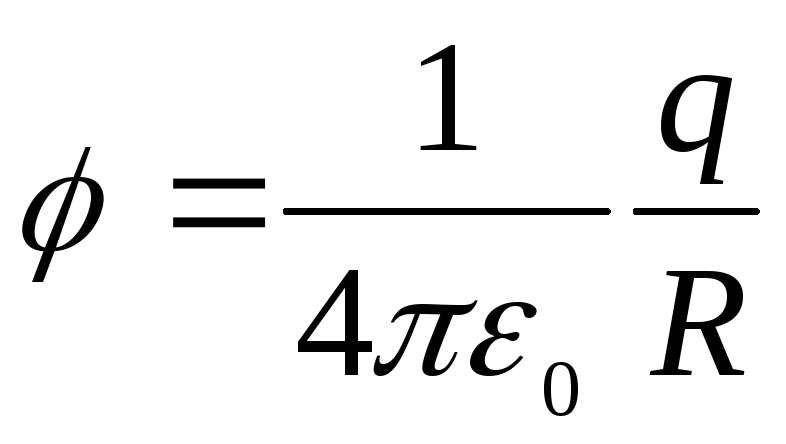Jos järjestelmä on luonut kentän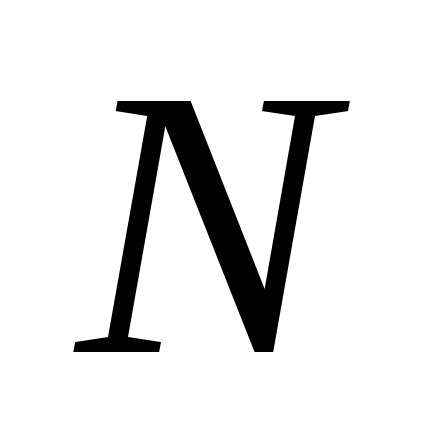 
pistemaksut sitten
,
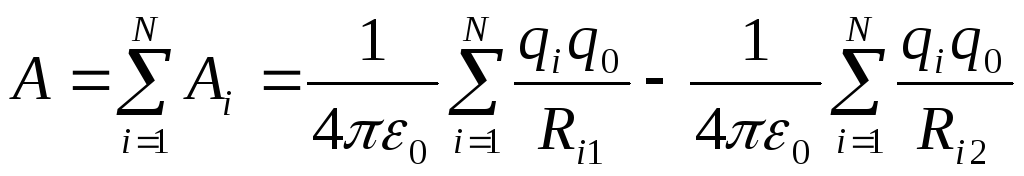jossa 
- etäisyys latauksesta 
alkuperäiseen latausasentoon ,
- etäisyys latauksesta lopulliseen latausasentoon (lataus kentän voimien liikkeet).
Sitten varauksen potentiaalinen energia latausjärjestelmän alalla:
,
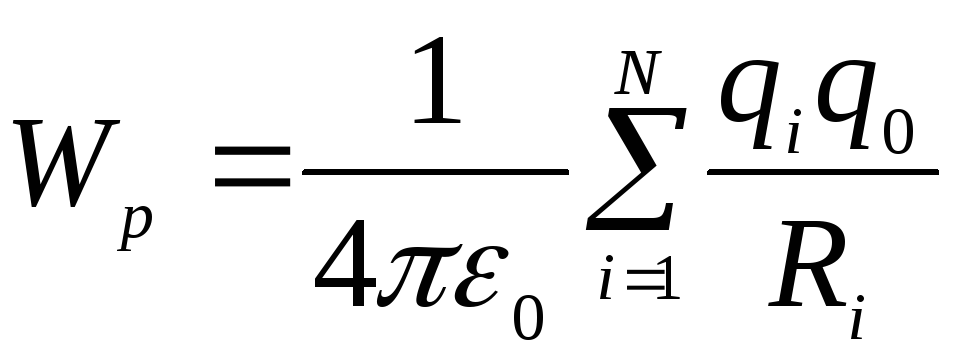ja potentiaalia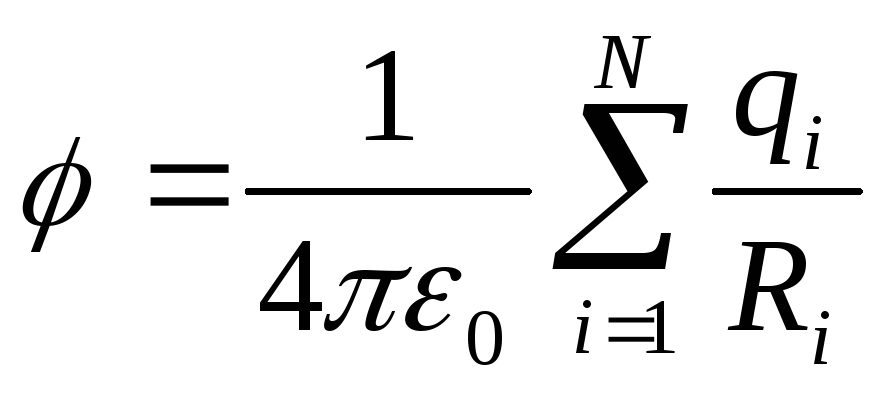 
latausjärjestelmän luoman kentän potentiaali on yhtä suuri kuin kunkin latauksen erikseen luomien potentiaalien algebrallinen summa.
Tietäen potentiaali, löydät varauksen potentiaalisen energian sähkökentässä:
.
Kenttätyöt veloitettuna:
Teos on yhtä suuri kuin potentiaalisten menetyksien lataus.
Jos varaus poistetaan pisteestä äärettömyyteen, kenttävoimien työ on yhtä suuri kuin
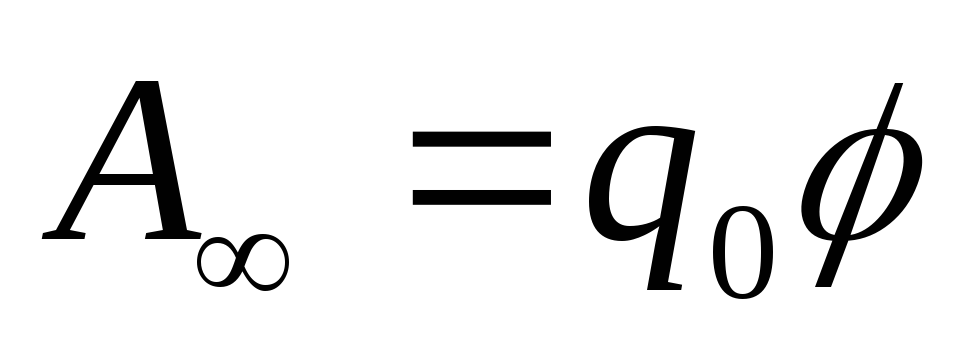
siksi potentiaali on numeerisesti yhtä suuri kuin työn suhde, jonka kenttävoimat suorittavat positiivisella varauksella, kun se poistetaan tietystä pisteestä äärettömyyteen, tämän varauksen suuruuteen. Mahdollisuus mitataan volteissa: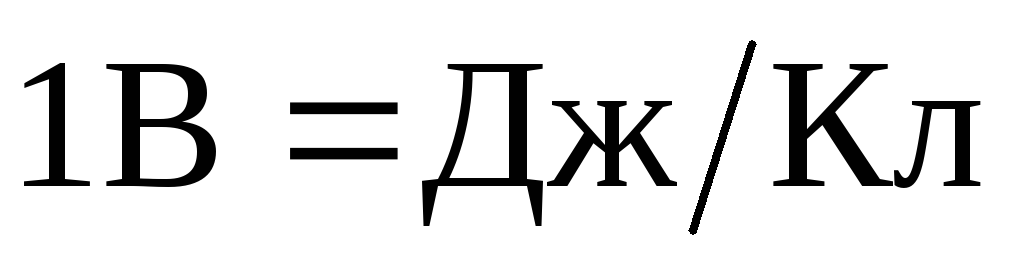 
.
1.5 Jännityksen ja potentiaalin välinen suhde
Sähkökenttä voidaan kuvata joko käyttämällä vektorimäärää (tehoominaisuus) tai skalaarilla 
(energiaominaisuus). Voima liittyy, kuten tiedät, potentiaaliseen energiaan:
,
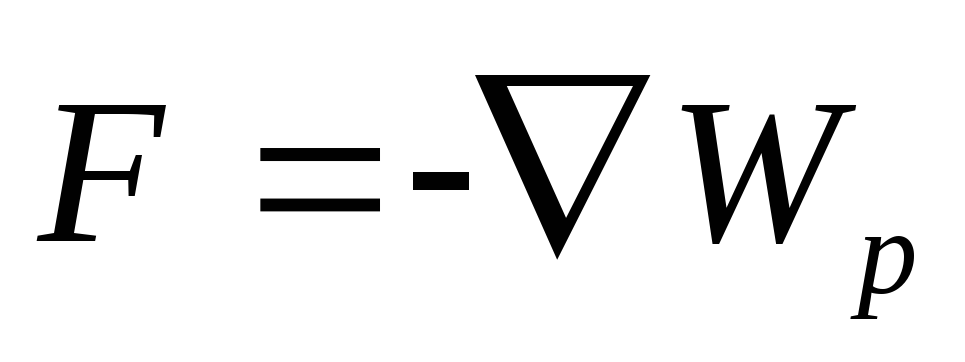jossa 
- Nablan operaattori, 
.
Sähkökentän varautuneelle hiukkaselle: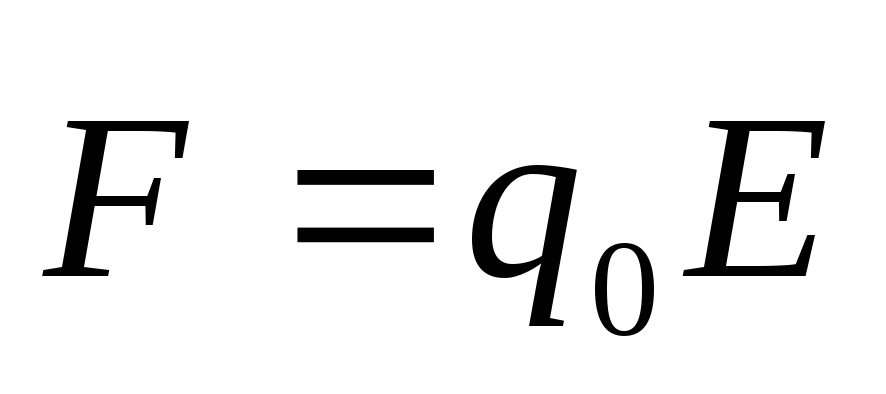 
,sitten 
,
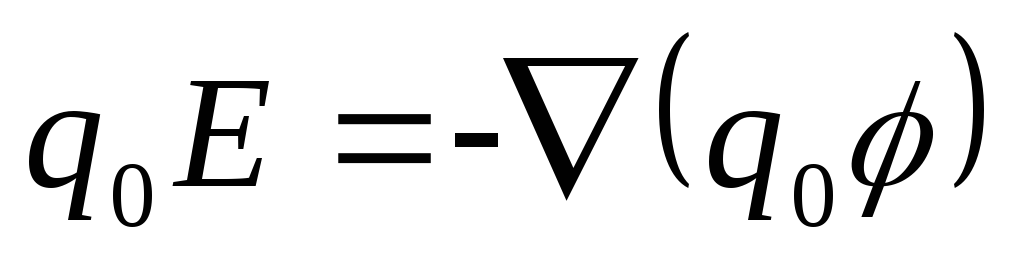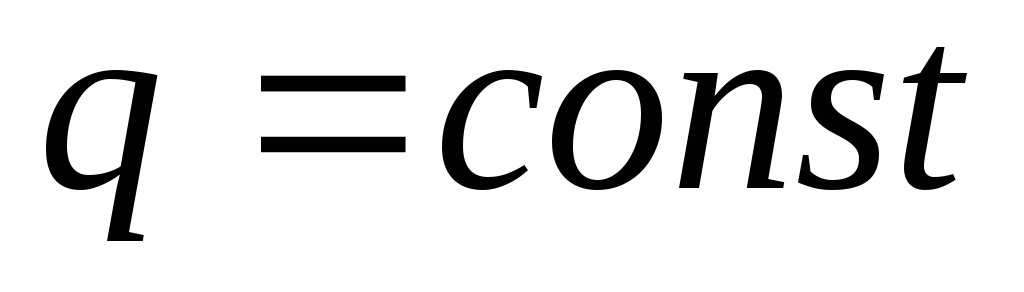sitten 
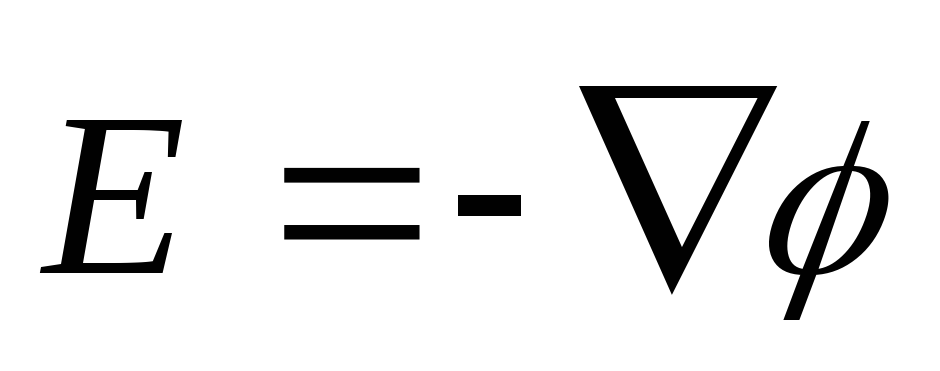- jännityksen ja potentiaalin suhde, tai 
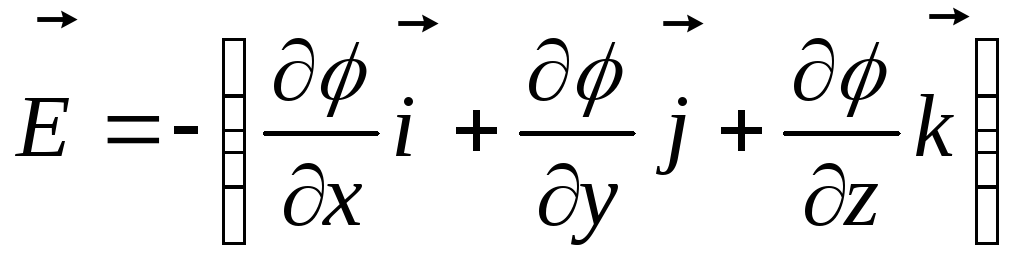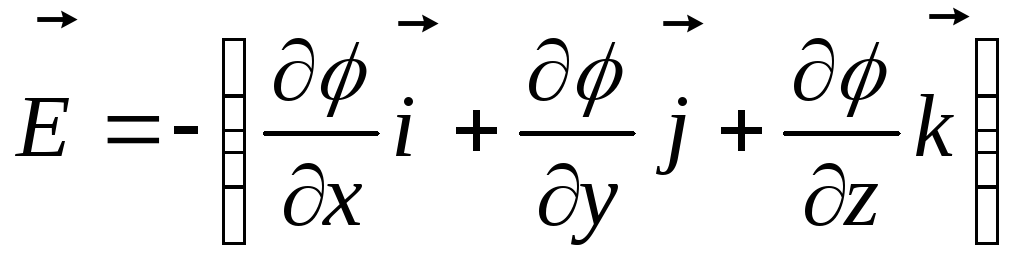tai tai 
-
vektori projektio mihin tahansa suuntaan 
yhtä suuri kuin potentiaalin vähentymisnopeus suuntaan
,
tai
.
Koska potentiaalin gradientti on suunnattu kohti sen kasvua, ja gradientin numeerinen arvo on tämän kasvun nopeuden mitta, voidaan sanoa, että sähkökentän voimakkuus on potentiaalin vähentymisnopeuden mitta tai yksinkertaisesti, että se on yhtä suuri kuin potentiaalin lasku.
Takaisin kentän määritelmään: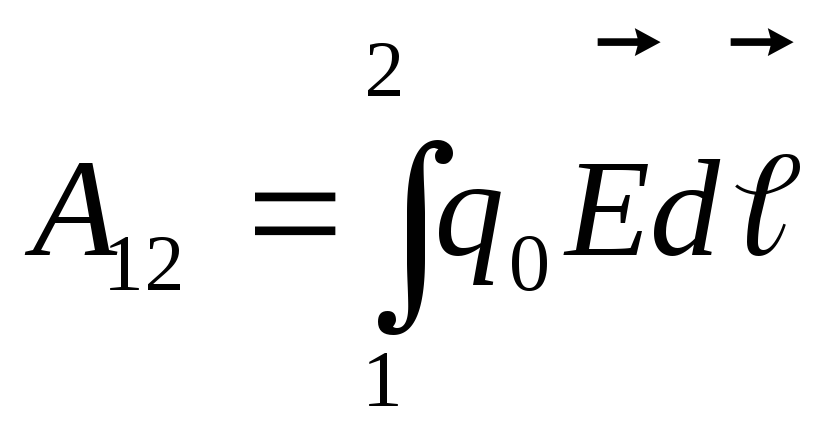 
,
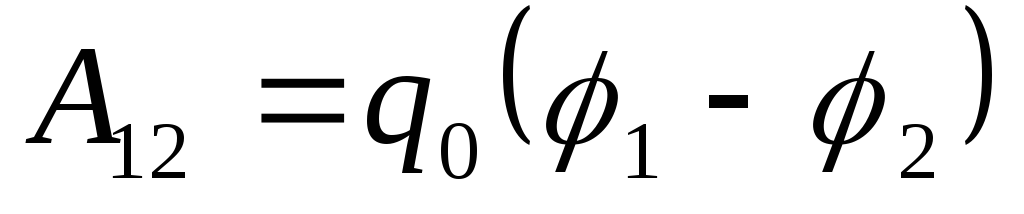, siten vektorin kierto
tontilla 1 \u003d 2 on 
. Integrointi voidaan ottaa mitä tahansa linjaa pitkin, joka yhdistää pisteitä 1 ja 2, koska työ ei riipu polusta.
Ohittaa suljetussa silmukass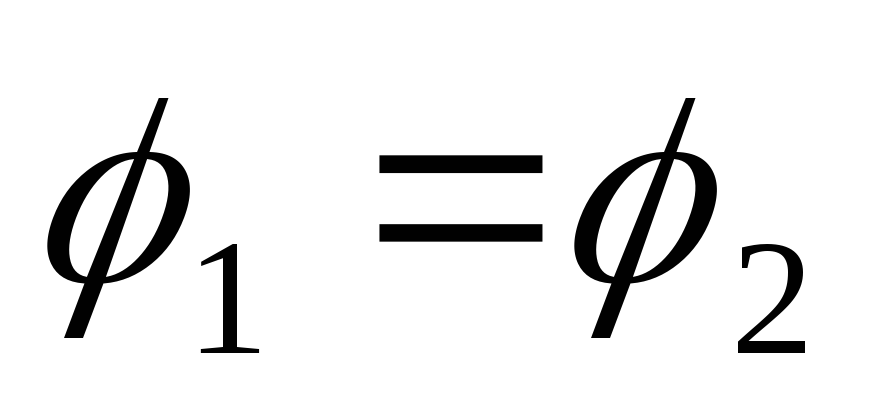a: 
ja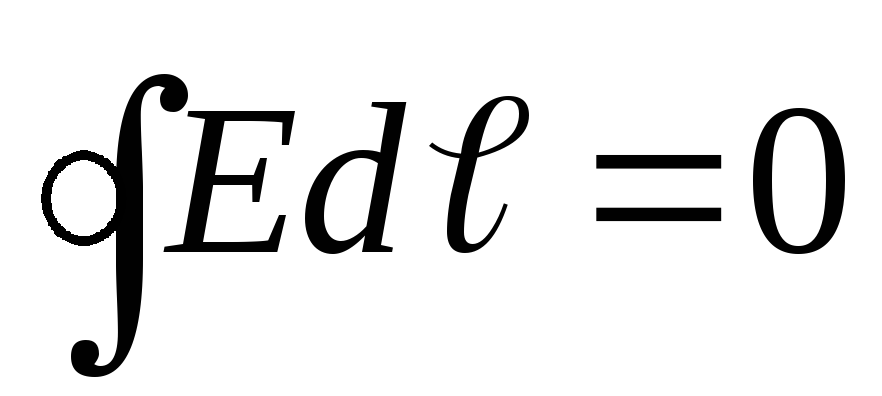 
- tuli lause sähköstaattisen kentän voimakkuusvektorin liikkeestä.
1.6. Potentiaalipotentiaaliset pinnat
Kuvitteellista pintaa, jonka kaikilla pisteillä on sama potentiaali, kutsutaan potentiaalipotentiaaliksi:
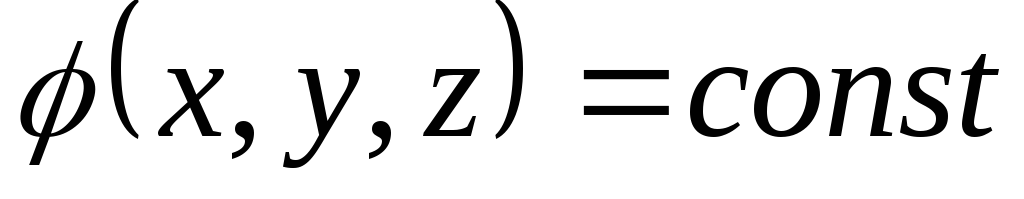
Potentiaalipotentiaalinen yhtälö.
Kun siirryt potentiaalipotentiaalista pintaa pitkin segmenttiin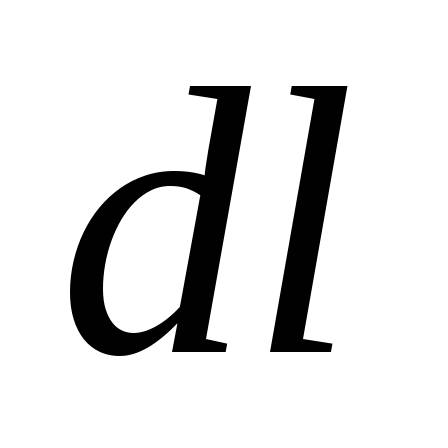 
potentiaali ei muutu 
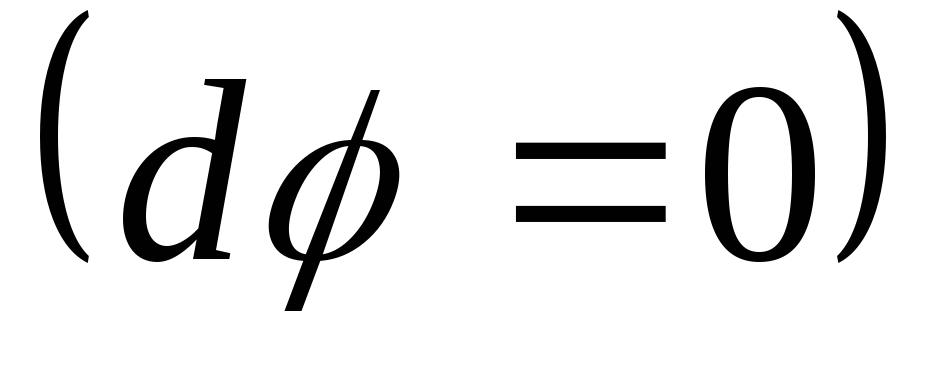. Siten vektorin komponentti, joka on tangentti pintaan yhtä suuri kuin nolla. Sitten vektori suunnattu normaaliin potentiaalipintaan jokaisessa sen pisteessä, ja kunkin pisteen jännitysviivat ovat kohtisuorassa potentiaalisten potentiaalisten pintojen kanssa.
Jos potentiaalipotentiaalipinnat on rakennettu siten, että kahden vierekkäisen pinnan potentiaaliero on sama, silloin potentiaalipotentiaalien tiheyttä voidaan käyttää arvioimaan kenttävoimakkuutta. Itse asiassa, mitä paksumpi potentiaalipinta, sitä suurempi 
sitä enemmän 
.
Homogeeniselle kentälle potentiaalipotentiaaliset pinnat ovat tasavälein sijaitsevien tasojen järjestelmä, joka on kohtisuora kentän suuntaan nähden.
Tarkastellaan pistevarauksen potentiaalista potentiaalista pintaa. Pistevarauksen potentiaali (kuva 1.4)
.
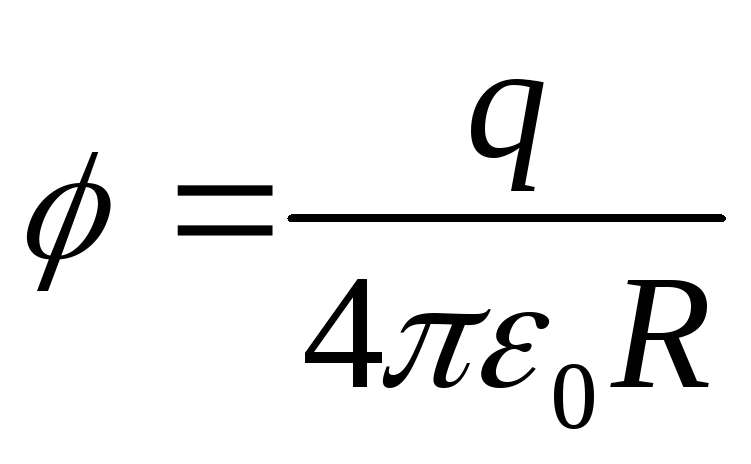Siten tämän varauksen potentiaalinen potentiaalipinta on säde- pallo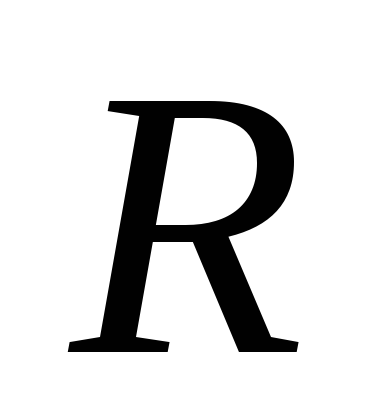 
keskitetty latauskohtaan. Voimajohdot, kuten aiemmin määrittelimme, poikkeavat radiaalisesti varauksesta, jos se 
, tai lähentyäksesi latausta, jos se on “-”. Se on vektori kohtisuorassa potentiaalisten potentiaalisten pintojen kanssa.
Aloitamme keskustelemalla potentiaalisesta energiasta, joka varauksella on sähköstaattisessa kentässä. Ensinnäkin on muistettava olosuhteet, joissa potentiaalisen energian käsite voidaan ottaa käyttöön.
4.1 Konservatiiviset voimat
Voimaa kutsutaan konservatiiviseksi (tai potentiaaliseksi), jos tämän voiman toiminta ei ole riippuvainen suuntauksen muodosta ja sen määrää vain vartalon alku- ja lopullinen sijainti.
Olkoon esimerkiksi keho, joka on konservatiivisen voiman vaikutuksessa, liikkua alusta
piste 1 loppupisteeseen 2 (kuva 16). Silloin voiman työ ~ riippuu vain asennosta
kohdat 1 ja 2 itse, mutta eivät kehon radalta. Esimerkiksi raiteille 1! A! 2 ja 1! b! Kuvion 2 mukaisesti A: n arvo on sama.
Kuva 16. Konservatiivisen vallan käsite
Huomaa, että konservatiivisen voiman työ millä tahansa suljetulla reitillä on nolla. Tosiaankin, poistetaan pisteestä 1 kulkureittiä 1 pitkin! A! 2 ja siirry takaisin rataa 2 pitkin! b! 1. Ensimmäisellä polulla voima suorittaa työn A, ja toisella polulla työ on A. Seurauksena on, että kokonaistyö on nolla.
Joten potentiaalisen energian käsite voidaan ottaa käyttöön vain konservatiivisen voiman tapauksessa. Potentiaalinen energia W tämä matemaattinen lauseke, riippuen kehon koordinaateista, siten, että voiman työ on yhtä suuri kuin tämän lausekkeen muutos miinusmerkillä:
Tai sama asia:
A \u003d (W2 W1) \u003d W1 W2:
Kuten näemme, konservatiivisen voiman työ on ruumiin alkuperäiseen ja lopulliseen asentoon laskettujen potentiaalienergia-arvojen ero.
Esimerkit konservatiivisista voimista ovat sinulle hyvin tunnettuja. Esimerkiksi painovoima on konservatiivinen. Jousivoima on myös konservatiivinen. Siksi voimme puhua maan yläpuolelle nousevan kehon potentiaalisesta energiasta tai epämuodostuneen jousen potentiaalisesta energiasta.
Mutta kitkavoima ei ole konservatiivinen: kitkavoiman toiminta riippuu suuntauksen muodosta eikä se ole nolla suljetussa polussa. Siksi kehon potentiaalista energiaa ei ole kitkavoiman kentässä.
4.2 Sähköstaattinen kenttäpotentiaali
Osoittautuu, että voima, jolla sähköstaattinen kenttä vaikuttaa varautuneeseen kappaleeseen, on myös konservatiivinen. Tämän voiman työtä, jota suoritetaan varauksen liikkuessa, kutsutaan sähköstaattisen kentän työksi. Siksi meillä on tärkein tosiasia:
Sähköstaattisen kentän toiminta ei riipu kulkureitin muodosta, jota pitkin varaus liikkuu, ja sen määräävät vain varauksen alku- ja lopullinen sijainti. Kentän työ suljetulla polulla on nolla.
Tätä tosiasiaa kutsutaan myös sähköstaattisen kentän potentiaaliksi. Kuten gravitaatiokenttä, myös sähköstaattinen kenttä on potentiaalinen. Sähköstaattisen kentän toiminta on sama kaikille reiteille, joita pitkin varaus voi liikkua yhdestä avaruuden kiinteästä pisteestä toiseen.
Tiukka matemaattinen todistus sähköstaattisen kentän potentiaalisuudesta on kouluopetuksen ulkopuolella. Voimme kuitenkin "fyysisellä tiukan tason tasolla" varmistaa tämän tosiasian paikkansapitävyyden seuraavilla yksinkertaisilla perusteluilla.
On helppo nähdä, että jos sähköstaattinen kenttä ei olisi potentiaalinen, silloin olisi mahdollista rakentaa jatkuva liikekone! Itse asiassa silloin olisi suljettu etenemissuunta, kun varaus siirtyisi, jota pitkin kenttä tekisi positiivisen työn (eikä muutoksia ympäröivissä vartaloissa tapahtuisi). Pyöritämme varaustamme tällä radalla, vedämme rajaton määrä energiaa tyhjästä ja kaikki ihmiskunnan energiaongelmat on ratkaistu :-) Mutta tätä valitettavasti ei noudateta, tämä on räikeä rikkomus energiansäästölaista.
Koska sähköstaattinen kenttä on potentiaalinen, voimme puhua varauksen potentiaalienergiasta tällä kentällä. Aloitetaan yksinkertaisella ja tärkeällä tapauksella.
4.3 Mahdollinen varausenergia yhtenäisellä kentällä
Maan yläpuolelle nostetun kehon potentiaalienergia on mgh. Tasaisen kentän varauksen tapaus osoittautuu hyvin samanlaiseksi tähän mekaaniseen tilanteeseen.
Tarkastellaan tasaista sähköstaattista kenttää E, jonka jännitysviivat on suunnattu X-akselia pitkin (kuva 17). Anna positiivisen varauksen q siirtyä kenttälinjaa pitkin pisteestä 1 (koordinaatin x1 kanssa) pisteeseen 2 (koordinaatin x2 kanssa).
0 x 1 | |||
Kuva 17. Latausliike tasaisella kentällä
Kenttä vaikuttaa varaukseen voimalla ~, joka on suunnattu jännityslinjoja pitkin. työ
tämä voima, kuten on helppo nähdä, on yhtä suuri kuin:
A \u003d F (x2 x1) \u003d qE (x2 x1):
Mitä muuttuu, jos kohdat 1 ja 2 eivät ole samalla jännitysviivalla? Ei käy ilmi mitään! Kentän kaava pysyy samana. Vahvistamme tämän kuvion 5 avulla. 18.
0 x 1 | ||||
Kuva 18. Latausliike tasaisella kentällä
Siirrytään pisteestä 1 pisteeseen 2, valitaan polku 1!3! Kuvassa 2, jossa piste 3 on samalla voimalinjalla pisteen 1 kanssa. Sitten A32: n työ osassa 32 on nolla, koska liikumme kohtisuorassa voimaan nähden. Seurauksena on, että saamme:
A \u003d A13 + A32 \u003d A13 \u003d qE (x2 x1):
Näemme, että kentän toiminta riippuu vain varauksen alkuperäisen ja lopullisen aseman abskissista. Me kirjoitamme tuloksena olevan kaavan seuraavasti:
A \u003d qEx2 qEx1 \u003d ((qEx2) (qEx1)) \u003d (W2 W1) \u003d W:
Tässä W1 \u003d qEx1, W2 \u003d qEx2. Kenttätyö kaavan (8) mukaisesti on yhtä suuri kuin muutos miinusmerkillä
Tämä arvo on varauksen potentiaalienergia yhtenäisessä sähköstaattisessa kentässä. X osoittaa sen pisteen abskissan, johon potentiaalista energiaa haetaan. Tässä tapauksessa potentiaalienergian nollataso vastaa lähtöä x \u003d 0, ja se esitetään kuvioissa katkoviivalla, joka on kohtisuorassa jännitysviivoihin4 nähden.
Muista, että kun tarkastellaan q\u003e 0. Kaavasta (9) seuraa, että kun varaus liikkuu kenttäviivaa pitkin, potentiaalienergia pienenee kasvaessa x. Tämä on luonnollista: loppujen lopuksi kenttä tekee positiivisen työn hajottamalla varauksen, ja varauksen kineettinen energia kasvaa potentiaalienergian pienentymisen vuoksi.
On helppo osoittaa, että kaava (9) pysyy voimassa q: lle< 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.
Joten, tärkeä johtopäätös: potentiaalienergian kaavassa q tarkoittaa varauksen algebrallista arvoa (ottaen huomioon merkki), eikä sen moduulia.
4 Itse asiassa nollapotentiaalinen energia voidaan valita mistä tahansa. Toisin sanoen potentiaalienergia määritetään vain mielivaltaiseen additiovakioon C saakka, ts. W \u003d qEx + C. Tällaisessa epävarmuudessa ei ole mitään vikaa: potentiaalisella energialla itsessään on fyysinen merkitys, ja potentiaalienergioiden ero on yhtä suuri kuin kentän työ. Tässä erossa vakio C pienenee.
4.4 Pistevarausten vuorovaikutuksen potentiaalinen energia
Olkoon kahden pistevarauksen q1 ja q2 tyhjiössä etäisyydellä r toisistaan. Voidaan osoittaa, että niiden vuorovaikutuksen potentiaalienergia annetaan kaavalla:
kq1 q2 | ||||
Hyväksymme kaavan (10) ilman todisteita. Tämän kaavan kahdesta piirteestä tulisi keskustella.
Ensinnäkin, missä on potentiaalienergian nollataso? Loppujen lopuksi potentiaalinen energia, kuten kaavasta (10) voidaan nähdä, ei voi kadota. Mutta itse asiassa nollataso on olemassa, ja se on äärettömyydessä. Toisin sanoen, kun lataukset sijaitsevat äärettömästi kaukana toisistaan, niiden vuorovaikutuksen potentiaalienergian oletetaan olevan nolla (mikä on loogista, että tässä tapauksessa lataukset "eivät ole vuorovaikutuksessa").
Toiseksi, q1 ja q2 ovat jälleen varausten algebralliset arvot, ts. Varaukset ottaen huomioon niiden merkki.
Esimerkiksi kahden saman nimisen varauksen vuorovaikutusenergia on positiivinen. Miksi? Jos annamme heidän mennä, ne alkavat kiihtyä ja siirtyä pois toisistaan. Heidän kineettinen energia kasvaa, joten potentiaalinen energia vähenee. Mutta äärettömyydessä potentiaalinen energia katoaa ja koska se laskee nollaan, niin se on positiivinen.
Mutta vastakkaisten latausten vuorovaikutuksen potentiaalinen energia on negatiivinen. Itse asiassa, poistamme ne erittäin suurella etäisyydellä toisistaan \u200b\u200bniin, että potentiaalinen energia on nolla ja päästään irti. Lataukset alkavat kiihtyä, lähentyessä, ja potentiaalinen energia vähenee jälleen. Mutta jos hän oli nolla, niin mihin hän meni? Vain kohti negatiivisia arvoja.
Kaava (10) auttaa myös laskemaan maksujärjestelmän potentiaalienergian, jos varausmäärä on enemmän kuin kaksi. Voit tehdä tämän summaamalla kummankin varausparin energiat. Emme kirjoita yleistä kaavaa; kuvaamme paremmin mitä on sanottu yksinkertaisella kuviossa 19 esitetyllä esimerkillä.
Kuva 19. Kolmen varauksen vuorovaikutus
Jos varaukset q1, q2, q3 ovat kolmiossa, jonka sivut ovat a, b, c, niiden vuorovaikutuksen potentiaalienergia on:
kq1 q2 | kq2 q3 | kq1 q3 | |||||
4.5 potentiaalia
Kaavasta W \u003d qEx näemme, että varauksen q potentiaalienergia homogeenisessa kentässä on suoraan verrannollinen tähän varaukseen.
Näemme saman kaavasta W \u003d kq1 q2 \u003d r: pistevarauksen q2 kentässä olevan varauksen q1 potentiaalienergia on suoraan verrannollinen varauksen q1 arvoon.
jos sähkörunko toimiessaan sähköisesti varautuneisiin kappaleisiin, se pystyy suorittamaan liikkuvien varautuneiden kappaleiden työn. Pistevarauksen luoma sähköstaattinen kenttä on keskeinen, ts. Tällaisessa kentässä pistevaraukseen vaikuttava voima ohjataan suoraa linjaa pitkin, joka yhdistää varauslähteen ja testivarauksen. Aikaisemmin osoitimme, että mikä tahansa keskusvoima on potentiaalinen, ts. Tämän voiman toiminta ei riipu radan muodosta, vaan sen määrää vain vartalon alku- ja lopullinen sijainti.
Muistutamme lyhyesti tämän tärkeimmän lausunnon todisteita. Anna pistetestauslaitteen q liikkua liikkumattoman varauksen Q luomassa keskikentässä (kuva 174). Testivaraukseen vaikuttava voima määrätään Coulombin lailla
Missä on vektori, joka on vedetty lähteen Q varauksesta pisteeseen A, jossa testivaraus sijaitsee. Kun varaus liikkuu varaukseen Q keskittyneiden ympyräkaarien pitkin (esimerkiksi pitkin kaaria AB, CD), sähkövoiman työ on nolla, joten voima ja siirtymävektorit ovat keskenään kohtisuorassa. Radiaalisuunnassa liikkuessa (esimerkiksi segmenttejä BC, DE pitkin) toiminta riippuu vain lähtö- ja loppuetäisyyksistä lähdevaraukseen. Joten sähköstaattisen kentän työskentely segmenttejä DE ja D1E1 pitkin liikkuessa on selvästi yhtä suuri. Tämän lausunnon kaunein todiste liittyy kentän symmetriaan - käännetään järjestelmämme lähteen läpi kulkevan akselin ympäri niin, että segmentti D1E1 osuu segmentin DE kanssa - kentän jakauma ei muutu, miksi kentän pitäisi toimia?
Koska superpositioperiaate pätee sähköstaattisen kentän voimakkuuteen, mikä tahansa sähköstaattinen kenttä on potentiaalinen. Tosiaankin, anna pistevaraus q olla kiinteäpistevarausten Q1, Q2, ..., QN järjestelmän luomassa sähkökentässä. Kun varaus siirtyy pieneen siirtymävektoriin, määritelmän mukaan sähkökenttä tekee työn missä
Tuloksena oleva liikkuvalle varaukselle q vaikuttava voima on yhtä suuri kuin kunkin kiinteän pistevarauksen puolella toimivien voimien summa Qk. Tämän voiman työ voidaan laskea kaavalla
Jotta voidaan laskea työ suuntauksen loppupäätä pitkin, on tarpeen jakaa polku pieniksi osiksi (kuva 175), sitten kaavan (1) avulla laskea työ jokaisessa pienessä osassa ja koota ne yhteen
. (2) Itse asiassa tämä määrä on kaksinkertainen, koska jokainen tuloksena oleva voima on kaavan (1) mukaisten voimien summa. Huomaa, että kaavassa (2) tuloksena oleva voima muuttuu, koska se lasketaan radan eri kohdissa.
Kuten aiemmin osoitimme, pistevarauksen sähkökentän toiminta ei riipu suuntauksen muodosta, toisin sanoen jokainen kaavan (1) termi ei riipu radan muodosta, joten koko summa ei riipu suuntauksen muodosta. Siten mikä tahansa sähköstaattinen kenttä on potentiaalinen.
Siksi sähköstaattisessa kentässä sijaitsevalle pistevaraukselle voidaan syöttää potentiaalinen vuorovaikutusenergia U (x, y, z). Tällä toiminnolla on seuraava fyysinen merkitys: sähkökenttä siirrettäessä pistevarausta pisteestä koordinaateilla (x1, y1, z1) toiseen, koordinaateilla (x2, y2, z2) on sama kuin potentiaalienergian muutos, joka otetaan vastakkaisella merkillä:
. (3) Merkin muutos tässä määritelmässä on melko looginen: jos sähkökenttä on suorittanut positiivisen työn (A\u003e 0), sen energia vähenee (ΔU< 0). Для вычисления работы силы взаимодействия между двумя точечными заряженными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (Рис. 176). Если построить зависимость силы взаимодействия между зарядами от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (Рис. 177). Зависимость силы sähköstaattinen vuorovaikutus etäisyydeltä se on samanlainen kuin gravitaation vuorovaikutusvoima, yhdellä merkittävillä eroilla: gravitaatiovoima on aina houkutteleva voima ja sähköinen voi olla sekä houkutteleva voima että heijastusvoima. Erityisesti kaksi positiivista panosta torjuvat. Siksi sähkökentän työn lauseke on samanlainen kuin gravitaatiovoiman vaikutuksen kaava, mutta sillä on vastakkainen merkki
Tämä työ on yhtä suuri kuin vuorovaikutuksen potentiaalienergian lasku, ts. Tästä lausekkeesta voimme määrittää kahden pistevarauksen sähköstaattisen vuorovaikutuksen potentiaalisen energian lausekkeen. (4) Tällä määritelmällä kahden saman merkin varauksen potentiaalinen vuorovaikutusenergia on positiivinen ja pyrkii nollautumaan kappaleiden välisellä äärettömällä etäisyydellä. Vastakkaisten merkkien varausten vuorovaikutusvoima on suunnattu vastakkaiseen suuntaan, joten tämän voiman työ lisättäessä etäisyyttä varausten välillä on negatiivinen. Meidän ei kuitenkaan tarvitse tehdä lisävarauksia, koska kaava (4) ottaa automaattisesti huomioon maksujen merkit - jos varaukset ovat vastakkaisia, niin niiden tuote (vastaavasti energia) on negatiivinen. Merkillä varausten vuorovaikutuksen potentiaalisesta energiasta on hyvin selkeä merkitys. Saman merkin varaukset torjuvat siksi, kun ne “hajoavat” äärettömän suuren matkan päässä, sähkökenttä tekee positiivista työtä - siksi aluksi näiden varausten järjestelmällä on kyky tehdä työ, joten sen energia on positiivinen, kun varaukset siirtyvät toisistaan, niiden energia laskee nollaan. Vastakkaisten merkkien latauksia houkutellaan, jotta niiden poistamiseksi äärettömän suurelle etäisyydelle ulkoisten voimien on tehtävä positiivista työtä. Tässä tapauksessa varausparin energian tulisi kasvaa, joten aluksi se on negatiivinen ja kun varaukset poistetaan toisistaan, se nousee nollaan. Yleensä tavanomainen tilanne - vetovoima vastaa negatiivista energiaa ja torjuminen - positiivista. Huomaamme vain, että tällainen näyttö on pätevää vain valittaessa nolla potentiaalienergian tasoa äärettömyyteen. Kaava (4) määrittelee kahden pistevarauksen omaavan ruumiin vuorovaikutuksen potentiaalienergian. Rungon Q ja q varausten arvot syötetään, kuten voidaan olettaa, tähän kaavaan symmetrisesti. Latausten jakaminen lähdelataukseksi ja testivaraukseksi on ehdollista, ne voidaan vaihtaa kokonaan. Siksi tämä kaava on edullista kirjoittaa symmetrisessä muodossa: kahden pistevarauksen q1 ja q2 vuorovaikutusenergia on yhtä suuri kuin (5), ja kentän tekemä työ on järkevää latausten välisellä etäisyydellä r: stä äärettömyyteen riippumatta siitä, liikkuuko ensimmäinen lataus vai toinen. , tai molemmat lataukset liikkuvat lopulta riippumatta molempien latausten liikkumistavoista. Lisäksi ei voida sanoa, mihin tiettyyn varaukseen tämä energia "kuuluu", osoitamme myöhemmin, että varausten vuorovaikutusenergia on osa itse sähköstaattisen kentän energiaa, toisin sanoen sitä "rasvataan" koko avaruudessa, missä näiden varausten luoma kenttä on. Jos järjestelmä koostuu useammasta kuin kahdesta varauksesta, näiden latausten vuorovaikutusenergian laskemiseksi on tarpeen laskea yhteen kaikkien varausparien vuorovaikutusenergiat.
tässä Uik on etäisyydellä rik toisistaan \u200b\u200bsijaitsevien varausten qi ja qk vuorovaikutusenergia (kuva 178).
40 Kysymys:
Sähköstaattinen kenttä - el. liikkumattoman varauksen kenttä.
Latauksella toimiva kaveri liikuttaa sitä ja tekee raboa. Yhtenäisessä sähkökentässä Fel \u003d qE on vakio
Kentän työ (sähkövoima) ei riipu radan muodosta ja suljetusta polusta \u003d nolla.
LAATUNUN RUNNAN potentiaalinen ENERGIA HOMOGEENISESSA ELEKTROSTAATTISESSA ALASSA
Sähköstaattinen energia - varautuneiden elinten järjestelmän potentiaalinen energia (koska ne ovat vuorovaikutuksessa ja pystyvät suorittamaan työn loppuun).
Koska kentän työ ei ole riippuvainen suuntauksen muodosta, niin samanaikaisesti
vertaamalla työkaavoja saadaan potentiaalinen varausenergia yhtenäisessä sähköstaattisessa kentässä
Jos kenttä tekee positiivista työtä (voiman linjoja pitkin), niin potentiaalinen energia
varautunut keho vähenee (mutta energian säilyvyyslain mukaan kineettinen energia kasvaa) ja päinvastoin.
SÄHKÖISET ALAT Potentiaalinen
Energiaominaisuus el. kenttään.
Sama kuin kentän varauksen potentiaalisen energian suhde tähän varaukseen.
Skaalaarimäärä, joka määrittää varauksen potentiaalisen energian missä tahansa kohdassa el. kenttään.
Mahdollista arvoa pidetään suhteessa valittuun nollatasoon.
DP (tai muuten VOLTAGE)
Tämä on potentiaaliero varauspolun alku- ja loppupisteissä.
Kahden pisteen (U) välinen jännite on yhtä suuri kuin näiden pisteiden potentiaaliero ja on yhtä suuri kuin kentän työ yksikkövarauksen siirtämisessä.
MAHDOLLISEN Jännityksen ja potentiaalien erottelun välinen viestintä
Laskemme sähkövarausten potentiaalienergian yksinkertaisimmissa, mutta erittäin tärkeissä erityistapauksissa.
Potentiaalinen varausenergia tasaisessa kentässä Anna varauksen q siirtyä tasaisella sähkökentällä intensiteetillä E pisteestä 1 pisteeseen 2. Pisteen 1 sijainti määritetään sädevektorilla ja pisteen 2 sädevektorilla r2. Lataukseen F \u003d qE vaikuttava voima on vakio. Voiman F toiminta ei riipu kulkureitin kytkentäpisteiden 1 ja 2 muodosta. Tämä seuraa sähköstaattisen kentän potentiaalin yleisestä todisteesta. Todistus on mahdollista suorittaa suorilla laskelmilla töistä, kun varaus liikkuu eri polkuja samalla tavalla kuin se tehtiin mekaniikassa painovoimien varalta. Nyt emme tee sitä.
Helpoin tapa laskea työ, jos varaus liikkuu suoraa linjaa pitkin kytkentäpistettä 1 ja pistettä 2 (kuva 1.78). Siirtymävektori Дг \u003d r2 - rv Work on yhtä suuri kuin voiman ja siirtymän skalaarituote:
A \u003d F Ar ^ qE (r2-r1) \u003d qE r2-qE vv (1.18.1)
Toisaalta kohdan (1.17.1) mukaan A \u003d ~ (W 2 ~ Vertaamalla lausekkeita (1.18.1) ja (1.17.1) saamme potentiaalisen varauksen energian lausekkeen tasaisella kentällä:
Wp ~ -qE g (1.18.2)
Yhdenmukainen kenttä luodaan etenkin vastakkaisten merkkien varauksia kantavien rinnakkaislevyjen väliseen tilaan (kuva 1.79). On luonnollista valita koordinaattijärjestelmä siten, että X-akseli on kohtisuora levyihin nähden. Silloin ulkonemat E „ja E ovat yhtä suuret kuin nolla ja
at z
kumpikaan (1.18.2) ei ole muotoa:
Wp \u003d -q (Exx + Eyu + Ezz) \u003d ~ qExx. (1.18.3)
Kaava (1.18.3) on samanlainen kuin kaava Wp \u003d mgh kehon potentiaalienergian suhteen Maan pinnan yläpuolelle. Massan roolilla on varaus, painovoiman kiihtyvyydet ovat kentän voimakkuutta ja korkeuden sijasta x-koordinaatti. Mutta energian merkki on erilainen: miinus plusin sijaan. Tässä on kohta. Massa on aina positiivinen, ja painovoima on välttämättä suunnattu pystysuoraan alaspäin. Nämä olosuhteet huomioon ottaen kaava Wp \u003d mgh kirjoitettiin. Se sisältää vapaan pudotuksen kiihtyvyysmoduulin, ja korkeus h mitataan maan pinnasta. Kaava (1.18.3) on yleisempi. Varaus q voi olla sekä positiivinen että negatiivinen; kentänvoimakkuus voidaan suunnata mihin tahansa, ja sen projektiolla voi olla joko positiivinen tai negatiivinen arvo riippuen koordinaattijärjestelmän valinnasta.
Erityisesti, jos kenttävoimakkuus E on suunnattu pystysuoraan alas ja X-akseli ylöspäin, niin
Wp \u003d qE \\ x \\ (1.18.4)
tarkalleen lausekkeen Wp \u003d mgh mukaisesti.
Jos sähkökenttä tekee positiivista työtä, varautuneen rungon energia kentässä vähenee: AW 0. Tämä varautuneen hiukkasen liike on samanlainen kuin heitetyn kiven liike. Tässä tapauksessa hiukkasen potentiaalienergia kasvaa ja kineettinen energia vähenee: hiukkanen hidastuu.
Potentiaalinen energia nolla
Potentiaalienergia sähköodynamiikassa määritetään, kuten mekaniikassakin, mielivaltaiseen vakioon. Lausekkeen (1.18.2) sijasta voisimme kirjoittaa:
W \u003d -qE-r + C, (1,18,5)
missä C on mielivaltainen vakio. Tässä tapauksessa potentiaalienergian muutos pysyy samana, ja työ määrittelee tarkalleen potentiaalienergian muutoksen, eikä itse energia. Kirjoittamalla kaava (1.18.2), me tosiasiallisesti tasaamme vakion C nollaan. Tämä vastaa tiettyä nolla potentiaalienergian tasoa. Esimerkiksi kuvassa 1.79 esitetyssä tapauksessa potentiaalienergian katsotaan olevan nolla levyn B pinnalla. Mutta kuten painovoimien vaikutuksen tapauksessa, potentiaalienergian nollataso valitaan mielivaltaisesti. Voimme olettaa, että W on O etäisyydellä levystä B. Sitten
Wp \u003d -qExx-qExx y
Fysikaalinen merkitys ei ole itse potentiaalienergia, vaan sen arvojen ero, jonka määrää kentän työ, kun varaus siirtyy alkuperäisestä sijainnista lopulliseen.
Pistevarausten vuorovaikutuksen energia
Mekaniikan aikana saatiin lauseke pistekappaleiden vuorovaikutusenergialle:
ty ja »W \u003d -G ---.
Rg
Jos pistemassojen sijasta otamme kaksi vastakkaisella merkillä varustettua varausta q1 ja q2 (varaukset vetävät puoleensa), voimme saada samanlaisen lausekkeen niiden vuorovaikutuksen potentiaaliselle energialle:
w (1.18.6)
R g y
Saman merkin latausten (maksut hylkivät) potentiaalisen energian merkki on vastapäätä:
w (1.18.7)
R g y
Kaavat (1.18.6) ja (1.18.7) voidaan yhdistää yhdeksi, jos latausmoduulien sijasta otetaan niiden algebralliset arvot:
W. (1.18.8)
P r v "
Potentiaalisen energian merkki osoittautuu automaattisesti oikeaksi.
Jos varauksilla ql ja q2 on samat merkit, niin niiden vuorovaikutuksen potentiaalienergia on positiivinen (kuva 1.80, a). Se on suurempi, mitä pienempi etäisyys latausten välillä, koska työ, jonka Coulomb-joukot voivat tehdä, kun lataukset työnnetään pois toisistaan, on enemmän. Jos varauksilla on vastakkaisia \u200b\u200bmerkkejä, niin energia on negatiivinen ja sen maksimiarvo, nolla, saavutetaan, kun r -\u003e oo (kuva 1.80, b). Mitä suurempi r, sitä enemmän työtä houkuttelevat voimat suorittavat, kun lataukset lähestyvät toisiaan.
Kuva 1.80
Kun kirjoitetaan potentiaalienergiaa muodossa (1.18.8), potentiaalienergian nollataso on jo valittu. Uskotaan, että äärettömän kaukana olevien varausten potentiaalienergia on nolla: Wp - »0 as r -» oo. Tämä nollatason valinta on kätevä, mutta ei vaadittava. Lausekkeen (1.18.8) sijasta voitaisiin kirjoittaa samalla menestyksellä
(1.18.9)
p r y
missä C on mielivaltainen vakio. Tämä osoittaa, että potentiaalienergian positiivisella tai negatiivisella arvolla ei ole erityistä fyysistä merkitystä. Potentiaalisen energian merkki määritetään, kun kiinnitetään mielivaltainen vakio C. Muuttamalla C: n arvoa, voimme muuttaa Wp: n merkkiä tietyllä etäisyydellä r varausten välillä.
Pistevarausjärjestelmän potentiaalinen energia
Pistevarausjärjestelmän potentiaalienergia qv q2, ..., qN on yhtä suuri kuin kaikkien vuorovaikutuksessa olevien varausparien potentiaalienergioiden summa. Kolmelta maksulta
w kbSi + hbS * + hw3 l
R G1,2 G1,3 G2,3
Todista se itse seuraavan tempun avulla. Aluksi varaukset q2 ja qz sijaitsevat äärettömän suurella etäisyydellä varauksesta qv. Sitten varaus q2 siirtyy pisteeseen, joka sijaitsee etäisyydellä gl 2 ensimmäisestä latauksesta. Sen jälkeen varaus qz siirtyy pisteeseen, joka on etäisyydellä r1 3 ensimmäisestä latauksesta ja r2 3 toisesta. On tarpeen laskea näiden liikkeiden aikana suoritettujen Coulomb-voimien työ ja verrata se potentiaalienergian muutokseen vastakkaisella merkillä.
Yleisessä tapauksessa N veloittaa
N N
Wp \u003d I llk7rh\u003e (1.18.11)
i \u003d lfc \u003d l (i * k)
missä r; k on mustenumeroiden varausten välinen etäisyys. Koeffi- 1
2 saadaan siitä tosiasiasta, että summaamalla potentiaalienergia otetaan huomioon kahdesti identtisen muodossa
ri, k rk, i
Mahdolliset energiakaavat sähkövaraus homogeenisessa kentässä (1.18.2) ja kahden pisteen varauksen (1.18.8) kohdalla on suositeltavaa muistaa. Niitä löytyy melko usein.
? 1. Onko mahdollista luoda sähköstaattinen
le, jonka jännitysviivat ovat yhdensuuntaiset ^ ^ ^ ^ ^ ^ ^
ovat löysät, ja ikäjännityksen moduuli -
kohtisuoraan suuntaan
niyam (kuva 1.81)? Kuva 1,81
Piirrä kuvaaja vastakkaisesti varautuneiden hiukkasten potentiaalienergian riippuvuudesta etäisyydeltä edellyttäen, että kaavan (1.18.9) mielivaltainen vakio C on positiivinen.
Miltä kaava (1.18.8) näyttää, jos varaukset ovat väliaineessa, jonka dielektrisyysvakio on є?